Chương 7: Phép biến đổi Laplace và ứng dụng

Chia sẻ: Nguyễn Trọng Tích | Ngày: | Loại File: PDF | Số trang:38

Thêm vào BST

Báo xấu

488
lượt xem 93
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Chương 7: Phép biến đổi Laplace và ứng dụng cung cấp cho người học khái niệm hàm biến phức; khái niệm gàm gốc, hàm ảnh; phép biến đổi Laplace, phép biến đổi Laplace ngược; các tích phân của phép biến đổi Laplace; khái niệm tích chập, ảnh của tích chập; một số phương pháp tìm hàm gốc;... Mời các bạn cùng tham khảo.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Chương 7: Phép biến đổi Laplace và ứng dụng

Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 1 Chöông 7 PHEÙP BIEÁN ÑOÅI LAPLACE VAØ ÖÙNG DUÏNG Trong chöông naøy , baïn seõ hoïc ♦ Khaùi nieäm haøm bieán phöùc. ♦ Khaùi nieäm haøm goác, haøm aûnh. ♦ Pheùp bieán ñoåi Laplace, pheùp bieán ñoåi Laplace ngöôïc. ♦ Caùc tính chaát cuûa pheùp bieán ñoåi Laplace. ♦ Khaùi nieäm tích chaäp, aûnh cuûa tích chaäp. ♦ Moät soá phöông phaùp tìm haøm goác. ♦ ÖÙng duïng pheùp bieán ñoåi Laplace ñeå giaûi phöông trình vi phaân, moät soá phöông trình tích phaân, heä phöông trình vi phaân. ………………………………………………………………………………………………………………………………………………………………… §1. PHEÙP BIEÁN ÑOÅI LAPLACE 0. 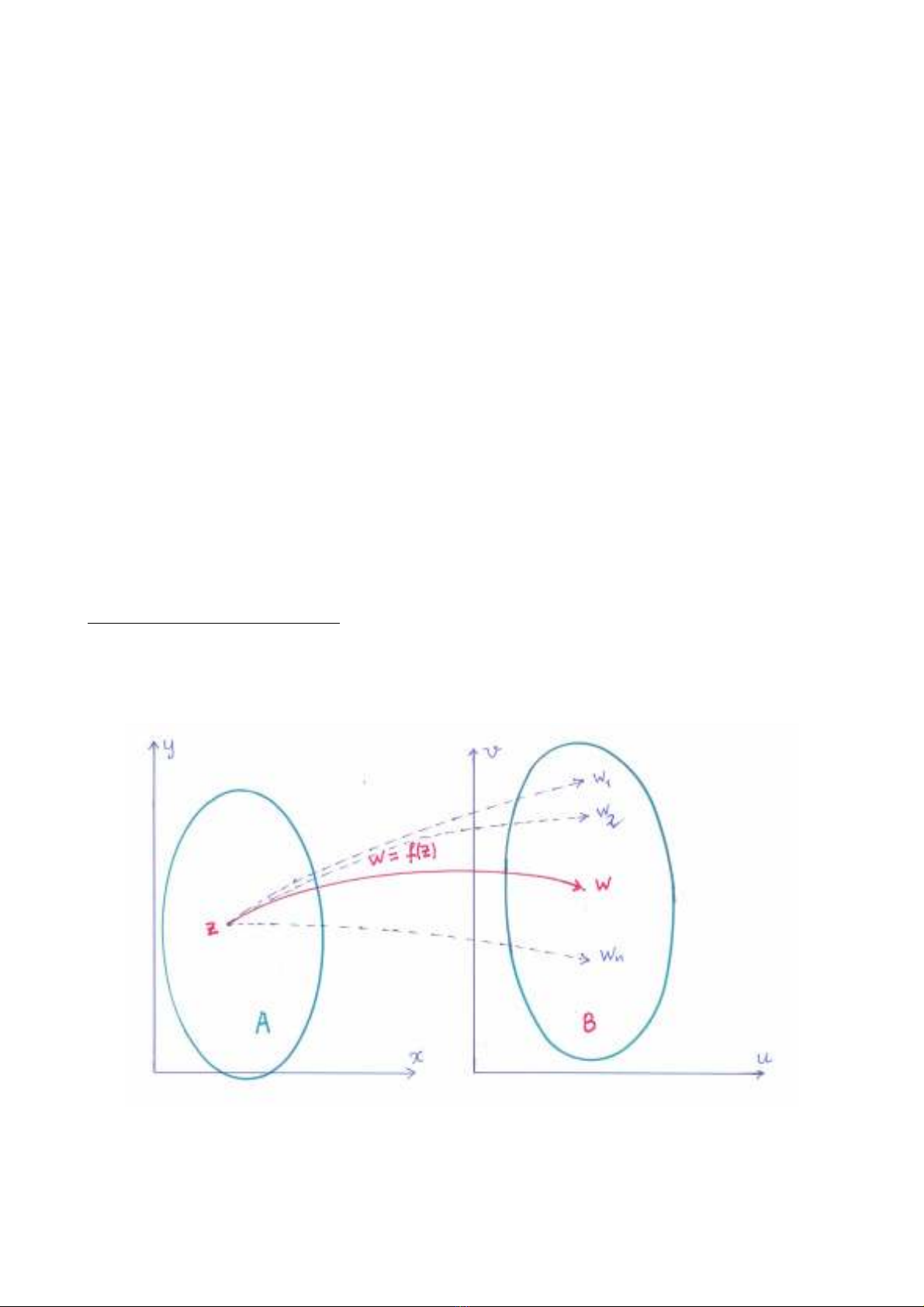Khaùi nieäm haøm bieán phöùc Giaû söû A laø taäp hôïp ñieåm trong maët phaúng phöùc z. Neáu coù moät qui taéc, goïi teân laø f , maø moãi soá phöùc z ∈A , töông öùng vôùi moät hoaëc nhieàu soá phöùc xaùc ñònh w , thì ta noùi treân taäp A ñaõ xaùc ñònh moät haøm bieán phöùc w = f (z ) . ♦ Neáu moãi soá phöùc z ∈A, töông öùng vôùi duy nhaát moät soá phöùc xaùc ñònh w, thì ta noùi w = f (z ) laø haøm ñôn trò. ♦ Neáu moãi soá phöùc z ∈A, töông öùng vôùi hai hay nhieàu soá phöùc xaùc ñònh w, thì ta noùi w = f (z ) laø haøm ña trò.
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 2 ♦ Neáu w = f (z ) laø haøm bieán phöùc xaùc ñònh treân taäp A thì A goïi laø mieàn xaùc ñònh vaø taäp B = {w / ∃ z ∈ A thoûa f(z) = w} goïi laø mieàn giaù trò cuûa haøm bieán phöùc w = f (z ) . ♦ Sau naøy, khi noùi ñeán moät haøm phöùc w = f (z ) maø khoâng noùi roõ gì theâm thì ta xem ñoù laø haøm ñôn trò. Phaàn thöïc vaø phaàn aûo cuûa haøm bieán phöùc Cho haøm bieán phöùc w = f (z ) , töùc laø cho phaàn thöïc u vaø phaàn aûo v cuûa w. Neáu z = x + iy thì u vaø v laø hai haøm thöïc cuûa hai bieán soá ñoäc laäp x vaø y. Toùm laïi, cho haøm phöùc w = f (z ) , töông öùng cho hai haøm thöïc u = u(x, y) , v = v(x, y). z = x + iy w= f(z) ⇔ w = u(x, y) + iv(x, y) (2.1) Ví duï7.0 Tìm phaàn thöïc vaø phaàn aûo cuûa caùc haøm phöùc 1 b) w= z2 + 2i z a) w = z Giaûi 1 1 x − iy x −y a) w = = = 2 = 2 +i 2 z x + iy x + y 2 x +y 2 x + y2 x −y Vaäy u(x,y) = 2 , v(x,y) = . x + y2 x2 + y2 b) w = (x+iy)2 + 2i(x-iy) = x2 –y2 + 2ixy + 2ix + 2y = (x2 –y2+ 2y) + i(2xy + 2x) Vaäy u(x,y) = x2 –y2+ 2y , v(x,y) = 2xy + 2x ¡ Nhaéc laïi ♦ Luõy thöøa baäc n soá phöùc- Coâng thöùc Moivre Neáu z = r( cosϕ ± i sinϕ ) ta ñöôïc coâng thöùc luõy thöøa baäc n soá phöùc z n = [r(cosϕ ± isinϕ )]n = rn( cosnϕ ± i sinnϕ ) , ∀n∈ Z Coâng thöùc Moivre (cosϕ ± isinϕ ) n = cosnϕ ± i sinnϕ , ∀n∈Z ♦ Khai caên baäc n cuûa soá phöùc Cho soá phöùc z = r(cosϕ + isinϕ) ≠ 0. Khi ñoù n z laø soá phöùc w thoûa wn = z. Ñaët w = ρ(cosθ + isinθ) , ta coù ρn(cosnθ + isinnθ) = [ρ(cosθ + isinθ)]n = wn = z = r(cosϕ + isinϕ)
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 3 n ⎧ρ n = r ⎧ρ = r ⎪ ⇒⎨ ⇒ ⎨ ϕ + 2kπ . Suy ra , vôùi k ∈ Z ⎩nθ = + 2kπ, vôùi k ∈ Z ⎪⎩θ = n ϕ + k 2π ϕ + k 2π n z = n r (cos + i sin ); k = 0,1,2,..., n-1; n ∈ N+ n n Nhaän xeùt Caên baäc n cuûa moät soá phöùc z = r(cosϕ + isinϕ) ≠ 0 coù taát caû n giaù trò, chuùng coù bieåu dieãn hình hoïc laø n ñænh cuûa moät ña giaùc ñeàu n caïnh noäi tieáp ñöôøng troøn taâm 0 baùn kính laø n r . ♦ Coâng thöùc Euler- Daïng muõ cuûa soá phöùc Coâng thöùc Euler: cosϕ + isinϕ = eiϕ Daïng muõ soá phöùc: z = r(cosϕ + isinϕ) = reiϕ 0.1 Haøm ña thöùc w = anzn + an-1zn - 1 + .....+ a1z + a0 = P(z) vôùi an ≠ 0; a0, a1, ....., an laø caùc haèng soá phöùc, n laø soá nguyeân döông ñöôïc goïi laø baäc ña thöùc P(z). P( z) 0.2 Haøm phaân thöùc ñaïi soá w := vôùi P(z), Q(z) laø caùc ña thöùc. Q( z ) 0.3-Haøm muõ ♦ w = ez = ex + iy = ex(cosy + isiny) ez+2kπi = ez e2kπi ez(cos2kπ + isin2kπ) = ez , k ∈Z. ♦ 1 ≠ a ∈ R+ : az := ezlna Ví duï 2 .7 2z = ezln2 ; 2 3+i = e (3+i) ln2 = e3ln2 eiln2 = e3ln2 [cos(ln2) +isin(ln2)]. ¡ 0.4 -Caùc haøm löôïng giaùc − − eiz − e iz eiz + e iz sin z = ; cos z = 2i 2 sin z cos z tgz = ; cot gz = cos z sin z e − t + e t t →+∞ e − t − e t t →−∞ Vôùi t ∈ R , cos(it) = ⎯⎯⎯→ +∞ ; sin(it) = ⎯⎯⎯→ +∞ . ª 2 2 * Nhaän xeùt Caùc haøm sinz, cosz khoâng bò chaën treân . 0.5-Caùc haøm Hyperbolic − − ez − e z ez + e z shz = ; chz = 2 2 shz chz thz = ; coth z = chz shz 0.6 Caùc haøm logarit ♦ Neáu z = ew thì ta vieát w = lnz, goïi laø logarit töï nhieân cuûa z. z = reiϕ = rei(ϕ + k2π), k = 0, ± 1, ± 2, .... w= lnz = lnr + i(ϕ + k2π); k = 0, ± 1, ± 2,....
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 4 Vaäy w = lnz laø haøm ña trò. Vôùi moãi soá nguyeân k coá ñònh , ta seõ xaùc ñònh ñöôïc moät nhaùnh cuûa haøm, luùc ñoù haøm trôû thaønh ñôn trò. Nhaùnh chính cuûa haøm lnz , kyù hieäu laø Lnz, xaùc ñònh bôûi: Lnz = lnr + iϕ vôùi 0 ≤ ϕ < 2π ( hoaëc coù theå laáy -π < ϕ ≤ π). Haøm lnz laø haøm ngöôïc cuûa haøm ez . ♦ Neáu z = aw thì w = logaz, 0 < a≠ 1: W = log z = ln z a ln a 0.7-Caùc haøm löôïng giaùc ngöôïc Caùc haøm ngöôïc cuûa caùc haøm sinz, cosz, tgz, cotgz laàn löôït laø arcsinz, arccosz, arctgz, arccotgz; vaø xaùc ñònh nhö sau: 1 1 ⎛ 1 + iz ⎞ arcsin z = ln(iz + 1 − z 2 ) arctgz = ln⎜ ⎟ i 2i ⎝ 1 − iz ⎠ 1 1 ⎛ z + i⎞ arccos z = ln( z + z 2 − 1) arc cot gz = ln⎜ ⎟ i 2i ⎝ z − i ⎠ 0.8 -Caùc haøm Hyperbolic ngöôïc Caùc haøm ngöôïc cuûa caùc haøm shz, chz, thz, cothz laàn löôït laø sh −1z , ch −1z , th −1z , coth −1 z ; vaø xaùc ñònh nhö sau: 1 ⎛1+ z⎞ sh −1 z = ln( z + z 2 + 1) th −1 z = ln⎜ ⎟ 2 ⎝1− z⎠ 1 ⎛ z + 1⎞ ch −1 z = ln( z + z 2 − 1) coth −1 z = ln⎜ ⎟ 2 ⎝ z − 1⎠ 0.9 - Haøm luõy thöøa zα , α ∈ C ñöôïc ñònh nghóa bôûi zα := eαlnz Töông töï haøm ( f(z)) g(z) = g(z)lnf(z) . e 1- Haøm goác Haøm goác laø haøm phöùc bieán thöïc f(t) = u(t)+ iv(t), thoûa maõn 3 ñieàu kieän sau: (i) f(t) lieân tuïc hay lieân tuïc töøng khuùc treân toaøn truïc t (nhöõng ñieåm giaùn ñoaïn(neáu coù) thuoäc loaïi 1). (ii) f(t) = 0 khi t < 0. (iii) f(t) coù baäc muõ. Töùc laø, toàn taïi caùc soá M > 0, s ≥ 0 sao cho ∀t > 0 thì f (t ) ≤ Me st Soá s0 ≥ 0 sao cho baát ñaúng thöùc (iii) thoûa ∀s = s0 + ε (ε > 0) vaø khoâng thoûa vôùi s = s0 - ε (s0- caän döôùi chính xaùc cuûa s) ñöôïc goïi laø chæ soá taêng cuûa haøm f(t). Haøm goác f(t) khi t ¤ + ∞ roõ raøng hoaëc laø höõu haïn hoaëc | f(t) | taêng ra +∞ nhöng khoâng nhanh hôn haøm muõ e s0 t . Ví duï 7.1 a) Haøm baäc thang ñôn vò ( unit step function, Heavisite’s unit function): ⎧0 khi t 〈 0 u(t) := ⎨ ⎩1 khi t > 0
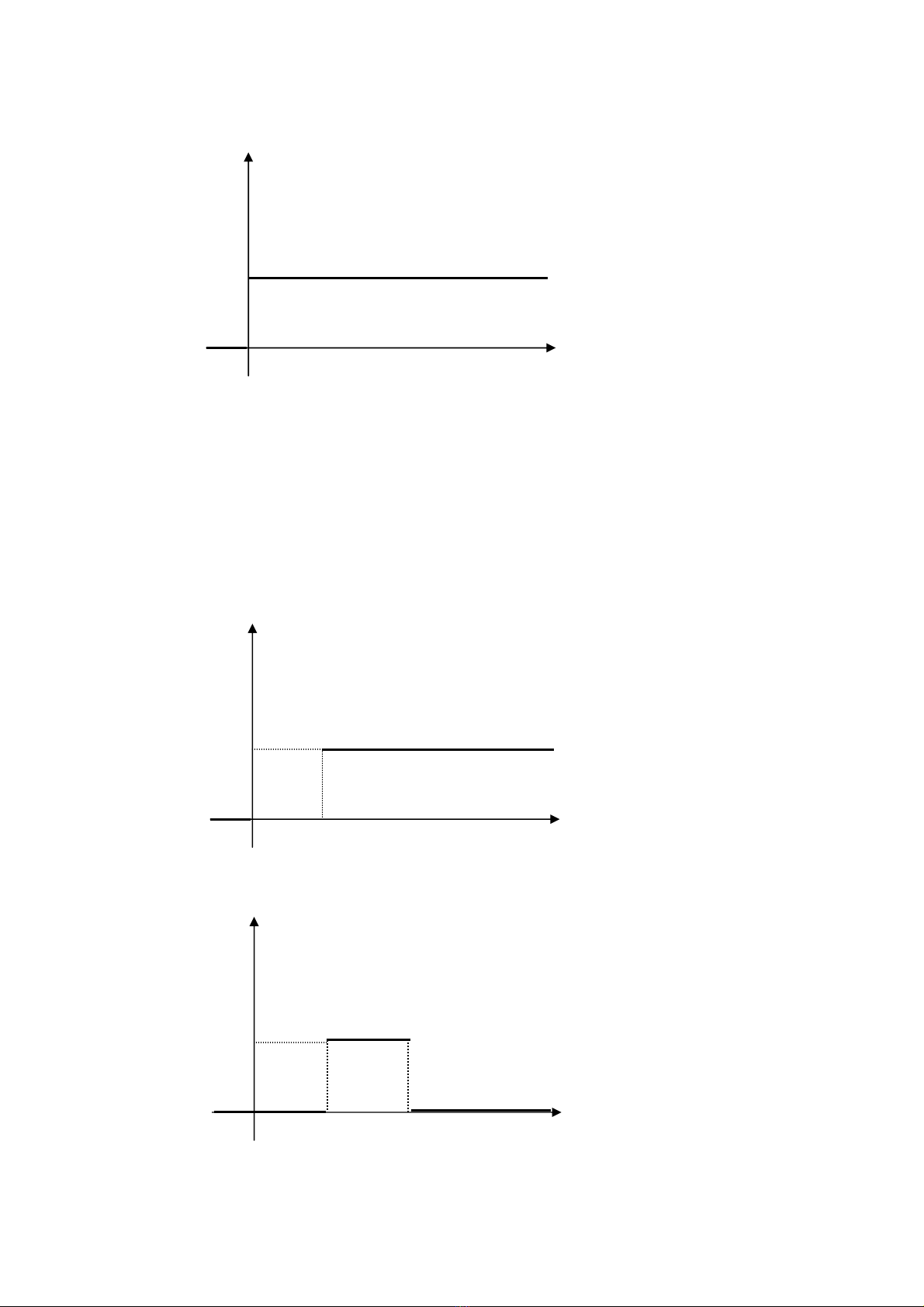
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 5 laø haøm goác vôùi chæ soá taêng so = 0. Ñoà thò cuûa haøm baäc thang ñôn vò ñöôïc veõ trong hình 7.1. u(t) 1 0 t Hình 7.1 ⎧ 0 khi t 〈 0 b) Haøm f(t) = ⎨ = u(t)sint laø haøm goác vôùi chæ soá taêng so = 0. ⎩sin t khi t > 0 ⎧0 khi t < 0 c) Haøm f(t) = ⎨ αt = u(t)eαt laø haøm goác vôùi chæ soá taêng so = α. ⎩e khi t > 0 ⎧0 khi t 〈a d) Haøm baäc thang ñôn vò treã a ñôn vò thôøi gian: u(t -a) := ⎨ laø haøm goác ⎩1 khi t > a vôùi chæ soá taêng so = 0. Ñoà thò cuûa haøm baäc thang ñôn treã a ñôn vò thôøi gian vò ñöôïc veõ trong hình 7.2. u(t-a) 1 0 a t Hình 7. 2 d) Haøm loïc: uab(t) = u(t-a) – u(t-b) , ñoà thò laø hình 7.3. uab (t) 1 0 a b t Hình7.3
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 6 Haøm naøy goïi laø haøm loïc vì khi nhaân moät haøm g(t) baát kyø vôùi noù, töùc laø g (t )[u (t − a) − u (t − b)] , thì haøm g(t) seõ bò khöû maát ngoaøi baêng thoâng a < t < b vaø giöõ nguyeân daïng trong baêng thoâng ñoù. Qui öôùc veà caùch vieát ñöôïc vieát goïn laø ♦ Haøm u(t) ⎯→ 1 ⎯⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ñöôïc vieát goïn laø ♦ Haøm u(t)sint ⎯→ sint ⎯⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ñöôïc vieát goïn laø ♦ Haøm u(t) eαt ⎯→ eαt ⎯⎯ ⎯ ⎯ ⎯ ⎯ ⎯ M ñöôïc vieát goïn laø ♦ Haøm u(t)g(t) ⎯⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯→ g(t) 2- Haøm aûnh Haøm aûnh cuûa haøm f(t) laø haøm F(p) cuûa bieán soá phöùc p = s + iσ xaùc ñònh bôûi tích phaân +∞ kyù hieäu Laplace F(p) := ∫ e − pt f (t )dt = L [f(t)] 0 Ví duï 7.2 a) Haøm aûnh cuûa haøm f(t) = 1 laø haøm: a +∞ a ⎡ e − pt ⎤ − pt − pt F(p) = ∫ e dt = lim a→+∞ ∫e dt = lim ⎢ a→+∞ ⎢ − p ⎥ ⎥ 0 0 ⎣ ⎦0 e − pa − 1 1 = lim = ( vôùi Rep > 0) a→+∞ −p p b) Haøm aûnh cuûa haøm f(t) = eαt laø haøm: a +∞ a ⎡ e (α − p)t ⎤ − pt αt (α − p )t F(p) = ∫ e .e dt = lim a→+∞ ∫e dt = lim ⎢ a→+∞ ⎢ α − p ⎥ ⎥ 0 0 ⎣ ⎦0 e ( α − p )a − 1 1 = lim = ( vôùi Rep > α) a→+∞ α−p p−α c) Haøm aûnh cuûa haøm f(t) = cost laø haøm: a +∞ a ⎡ e − pt (sin t − p cos t ) ⎤ F(p) = ∫ e − pt . cos tdt = lim ∫ e − pt cos tdt = lim ⎢ 2 ⎥ 0 a→+∞ 0 a→+∞ ⎢ ⎣ 1 + p ⎥⎦ 0 ⎡ e − pa (sin a − p cos a) + p ⎤ p = lim ⎢ 2 ⎥ = 2 ( vôùi Rep > 0) a→+∞ ⎢ ⎣ 1+ p ⎦⎥ 1+ p d) Töông töï haøm aûnh cuûa haøm f(t) = sint laø haøm:
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 7 +∞ 1 − pt F(p) = ∫ e . sin tdt = 1 + p 2 ( vôùi Rep > 0) ¡ 0 3- Ñònh lyù 7.1 Neáu f(t) haøm goác vôùi chæ soá taêng s0 thì haøm aûnh F(p) seõ hoäi tuï trong nöûa maët phaúng Re(p) = s > s0, vaø laø haøm giaûi tích (coù ñaïo haøm)trong mieàn ñoù. 4- Ñònh lyù 7.2 ( ñieàu kieän caàn cuûa haøm aûnh) Neáu F(p) laø haøm aûnh cuûa haøm f(t) vôùi chæ soá taêng s0 thì lim F ( p) = 0 . p →∞ p2 − 1 Ví duï7.3 Cho haøm F(p)= . Hoûi coù toàn taïi haøm goác f(t) sao cho F(p)=L [f(t)] khoâng? p2 + 1 Giaûi p2 − 1 Vì lim = 1 ≠ 0 , neân khoâng toàn taïi haøm goác f(t) sao cho F(p)= L [f(t)] . ¡ p →∞ p2 + 1 5. Pheùp bieán ñoåi Laplace 5.1- Pheùp bieán ñoåi Laplace 5.2- Pheùp bieán ñoåi Laplace ngöôïc Pheùp töông öùng Pheùp töông öùng ngöôïc laïi +∞ F(p) → f(t) sao cho L [f(t)] = F(p) f(t) → F(p) = ∫ e f ( t ) dt − pt ñöôïc goïi laø pheùp bieán ñoåi Laplace 0 ngöôïc . ñöôïc goïi laø pheùp bieán ñoåi Laplace hay Kyù hieäu: L -1[ F(p)] = f(t) ; L -1{ F(p)} toaùn töû Laplace. = f(t); F(p) → f(t), F(p) ≒ f(t) Kyù hieäu: L [f(t)] = F(p) ; L {f(t)} = F(p) ; f(t) → F(p) ; f(t) F[p] Nhaän xeùt Moãi bieán ñoåi Laplace luoân coù bieán ñoåi Laplace ngöôïc töông öùng vaø ngöôïc laïi. Ví du 7.4 (xem laïi ví duï 7.2) 1 ⎡1⎤ a) L [1] = ; L -1 ⎢ ⎥ = 1 ( vôùi Rep > 0) p ⎣p⎦ 1 ⎡ 1 ⎤ αt b) L [eαt] = ; L -1 ⎢ ⎥= e ( vôùi Rep > α) p−α ⎣p − α⎦
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 8 p -1 ⎡ p ⎤ c) L [cost] = ; L ⎢ ⎥ = cost ( vôùi Rep > 0) 1 + p2 ⎢⎣1 + p 2 ⎥⎦ 1 -1 ⎡ 1 ⎤ d) L [sint] = ; L ⎢ 2⎥ = sint ( vôùi Rep > 0) 1 + p2 ⎣⎢1 + p ⎦⎥ a +∞ a ⎡ − e − pt (pt + 1) ⎤ − pt − pt e) L [t] = ∫ e tdt = lim a→+∞ ∫e tdt = lim ⎢ a→+∞ ⎢ p 2 ⎥ ⎥⎦ 0 0 0 ⎣ ⎡ − e − pa (pa + 1) 1 ⎤ 1 ⎡1⎤ = lim ⎢ + ⎥ = ( vôùi Rep > 0). Do ñoù L -1 ⎢ 2 ⎥ = t . a→+∞ ⎢ ⎣ p2 p 2 ⎦⎥ p 2 ⎣p ⎦ b +∞ +∞ b ⎡ e − pt ⎤ − pt − pt − pt f) L [u(t-a)] = ∫e u(t − a)dt = ∫e dt = lim ∫e dt = lim ⎢ ⎥ b→+∞ b→ +∞ − p 0 a a ⎣ ⎦a − pb − pa − pa e −e e = lim = ( vôùi Rep > 0) ¡ b→ +∞ −p p 6 - Caùc tính chaát cô baûn cuûa pheùp bieán ñoåi laplace 6 .1 Tính chaát tuyeán tính Neáu L [f (t )] = F( p), L [g(t )] = G( p) vaø α , β laø caùc soá phöùc thì L [αf(t) +β g(t)] = αF(p) +β G(p ) Chöùng minh +∞ +∞ +∞ L [αf(t) +β g(t)] = ∫ e − pt [α f (t ) + β g(t )]dt = α ∫ e − pt f (t )dt + β ∫ e − pt g(t )dt 0 0 0 = α L [f(t)] + β L [g(t)] = αF(p) +β G(p ). ª Ví duï 7.5 5 3 1 a) L [5– 3e2t + 4sint] = 5L [1] -3 L [e2t] +4 L [sint] = - +4 p p−2 1 + p2 ⎡ e wt − e − wt ⎤ 1 wt -wt 1⎛ 1 1 ⎞ b) L [shwt] = L ⎢ ⎥ = ( L [e ] - L [e ] ) = ⎜⎜ − ⎟ ⎣ 2 ⎦ 2 2 ⎝ p − w p + w ⎟⎠ w = 2 , vôùi Rep > ⎢w⎢. p − w2 p c) Töông töï L [chwt] = 2 , vôùi Rep > ⎢w⎢. p − w2 e − pa − e − pb d) Aûnh cuûa haøm loïc : L [uab(t) ] = L [u(t-a)] - L [u(t-b)] = . p ¡ 6 .2 Tính chaát ñoàng daïng ( thay ñoåi thang ño)
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 9 1 1 t Neáu L [f (t )] = F( p) vaø α > 0 thì L [f(αt)] = p F ( ) , L -1[ F(αp)] = f( ) α α α α Chöùng minh +∞ p − pt 1 +∞ −α u 1 p L [f(αt)] = ∫ e f (αt )dt = ∫ e f (u)du = F ( ) . ª 0 α 0 α α Ví duï 7.6 ⎛ ⎞ ⎜ ⎟ 1 1⎜ 1 ⎟ w a) Bieát L [sint] = 2 . Khi ñoù L [sinwt] = ⎜ ⎟= 2 p +1 w ⎜ ⎛ p ⎞ ⎟ p + w2 2 ⎜1+ ⎜ w ⎟ ⎟ ⎝ ⎝ ⎠ ⎠ ⎛ p ⎞ ⎜ ⎟ p 1⎜ w ⎟ p b) Bieát L [cost] = 2 . Khi ñoù L [coswt] = ⎜ 2 ⎟ = 2 ¡ p +1 w p + w2 ⎜ 1 + ⎛⎜ p ⎞⎟ ⎟ ⎜ ⎟ ⎝ ⎝w⎠ ⎠ 6 .3 Tính chaát dòch chuyeån goác Neáu L [f (t )] = F( p) vaø a > 0 thì L [u(t-a)f(t-a )]= e− pa F(p); L -1[ e− pa F(p)]= u(t-a)f(t-a). ⎧0 khi t 〈 a Chuù yù : u(t -a) = ⎨ ⎩1 khi t > a Chöùng minh +∞ +∞ L [u(t-a)f(t-a )] = ∫e − pt f (t − a)u(t − a)dt = ∫ e − pt f (t − a)dt 0 a +∞ +∞ = ∫ e − p( u+a ) f (u)du = ∫ e − pa e − pu f (u)du ( ñaët u = t – a) 0 0 +∞ -pa = e − pa − pu ∫ e f (u)du = e F(p). ª 0 Ví duï 7.7 w w a) Bieát L [sinwt] = p2 + w2 . Khi ñoù L [u(t-2)sin(w(t-2))] = e− 2p p2 + w2 . 1 1 b) Bieát L [t] = 2 . Khi ñoù L -1[ e − p ] = u(t-1)(t-1). p p2 ¡ 6.4-Tính chaát dòch chuyeån aûnh Neáu L [f (t )] = F( p) , f(t) coù chæ soá taêng so , a laø soá phöùc
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 10 thì L ⎡eat f (t )⎤ = F(p-a) , vôùi Re(p-a) > so. ⎢⎣ ⎥⎦ Chöùng minh +∞ +∞ L ⎡eat f (t )⎤ = ∫ e − pt e at f (t )dt = ∫ e −( p−a)t f (t )dt = F(p-a) , vôùi Re(p-a) > so. ª ⎢⎣ ⎥⎦ 0 0 Ví duï 7.8 1 1 a) Bieát L [t] = 2 . Khi ñoù L [eαtt] = 2 . p ( p − α ) w αt w b) Bieát L [sinwt] = 2 . Khi ñoù L [ e sinwt] = . p + w2 ( p − α) 2 + w 2 p αt p−α c) Bieát L [coswt] = 2 . Khi ñoù L [ e coswt] = . p + w2 ( p − α) 2 + w 2 ⎡ p+4 ⎤ -1 ⎡ p−2 3 ⎤ d) L -1 ⎢ 2 ⎥=L ⎢ 2 2 + 2 . 2 2⎥ = e2tcos3t + 2e2tsin3t. ⎣ p − 4 p + 13 ⎦ ⎣ ( p − 2) + 3 ( p − 2) + 3 ⎦ ¡ 6.5 AÛnh cuûa haøm goác tuaàn hoaøn Ñoà thò haøm tuaàn hoaøn f(t) ñöôïc bieåu dieãn trong hình 7.4. f(t) Hình 7.4 Neáu f(t) laø haøm goác tuaàn hoaøn vôùi chu kyø T thì aûnh cuûa noù laø T 1 − pt f ( t ) dt F(p) = L [f(t)] = ∫e 1 − e− Tp 0 Chöùng minh +∞ T 2T − pt − pt − pt L [f(t)] = ∫ e f ( t )dt = ∫ e f ( t )dt + ∫ e f (t )dt +…… 0 0 T Trong caùc tích phaân sau ta laàn löôït ñoåi bieán t = u+T, t = u + 2T….. , ta ñöôïc T T T − pt -PT − pu -2PT − pu L [f(t)] = ∫ e f (t )dt +e ∫e f ( u)du + e ∫e f (u)du +…. 0 0 0 T T T = ∫e − pt f (t )dt +e-PT ∫ e − pt f (t )dt + e-2PT ∫ e − pt f (t )dt +… 0 0 0 T T 1 − pt f ( t ) dt . = (1+ e-PT + e-2PT +…………) ∫ e − pt f (t )dt = ∫e ª 0 1 − e− Tp 0
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 11 Ví duï 7.9 ⎧ t neáu 0 ≤ t < π Tìm aûnh cuûa haøm goác f(t) = ⎨ , f(t) tuaàn hoaøn chu kyø laø 2π. ⎩0 neáu π < t < 2 π f(t) π 0 π 2π 3π 4π 5π t Giaûi 2π π 1 − pt f (t )dt = 1 − pt tdt L [f(t)] = ∫ e ∫ e 1 − e− 2πp 0 1 − e− 2πp 0 π 1 ⎡ − e − pt ( pt + 1) ⎤ 1 ⎛ 1 e − pπ (pπ + 1) ⎞ = ⎥ = ⎜ ⎟ − 2πp ⎢ p 2 ⎜ p2 − p 2 ⎟ ¡ 1− e ⎣ ⎦ 0 1 − e− 2πp ⎝ ⎠ 6.6- Tính chaát ñaïo haøm haøm goác Neáu haøm goác f(t) coù ñaïo haøm ñeán caáp n vaø caùc ñaïo haøm cuõng laø haøm goác thì: L [f’(t)] = pF(p) - f(0) L [f’’(t)] = p2F(p) - pf(0) - f’(0) L [ f(n)(t)] = pnF(p) - pn-1f(0) - pn-2f’(0) - ........ - f(n - 1)(0) Trong ñoù F(p) = L [f(t)] . Chöùng minh Aùp duïng tích phaân töøng phaàn, ta coù +∞ +∞ [ ∞ ] L [f’(t)] = ∫ e − pt f ' (t )dt = f (t )e − pt 0 + p ∫ e − pt f (t )dt = pF(p) – f(0). 0 0 L [f’’(t)] = p L [f’(t)] - f’(0) = p[pF(p) – f(0)]-f’(0) = p2F(p) – pf(0) – f’(0) ª Ví duï 7.10 Giaûi phöông trình vi phaân: y′′ − y = t, y(0) = 1, y′(0) = 1. Giaûi Ñaët Y = Y(P) = L [y] . Bieán ñoåi Laplace hai veá phöông trình vaø aùp duïng tính chaát ñaïo haøm haøm goác ta ñöôïc: 1 P 2 Y − Py(0) − y ′(0) − Y = 2 P 1 1 1 1 ⇔ Y(P 2 − 1) = P + 1 + 2 ⇔ Y = + 2 − 2 P P −1 P −1 p
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 12 Bieán ñoåi Laplace ngöôïc hai veá: ⎡ 1 ⎤ −1 ⎡ 1 ⎤ −1 ⎡ 1 ⎤ y = L −1 [Y ] = L −1 ⎢ + L − L ⎣ P − 1⎥⎦ ⎢⎣ P 2 − 1⎥⎦ ⎢⎣ P 2 ⎥⎦ ⇔ y = e t + sht − t. Vaäy nghieäm cuûa phöông trình ñaõ cho laø: y = e t + sht − t. ¡ 6.7- Tính chaát ñaïo haøm haøm aûnh ( nhaân cho t) Neáu F(p) = L [f(t)] vaø Re(p) > s0 thì L [t f(t)] = -F’(p) , L [t2f(t)]= F’’(p)…....L [tnf(t)]= (-1)n F(n)(p) , Re(p) > s0. Ví duï 7.11 Tìm : a) L [tsinwt] b) L [tn] ' w ⎛ w ⎞ 2 pw a) Ta coù L [sinwt] = 2 ⇒ L [tsinwt] = - ⎜⎜ 2 ⎟⎟ = 2 p + w2 2 ⎝p +w ⎠ (p + w 2 ) 2 (n) 1 ⎛1⎞ n! b) L [1] = ⇒ L [tn] = L [tn.1] = (-1)n ⎜⎜ ⎟⎟ = ¡ p ⎝p⎠ p n +1 ⎧L [f (t )] = F( p)⎫ ⎡t ⎤ F ( p) 6.8- Tính chaát tích phaân haøm goác Neáu ⎨ ⎬ , thì L ⎢ ∫ f ( u )du ⎥= ⎩ Re( p ) > s 0 ⎭ ⎢ ⎥ p ⎣0 ⎦ 6.9- Tính chaát tích phaân haøm aûnh (chia cho t) ∞ Neáu L [f(t)] = F(p), Re(p) > s0 vaø ∫ F(u) du hoäi tuï trong nöûa maët phaúng Re(p) > s1 > s0 p ∞ ⎡ f (t ) ⎤ thì ∫ F(u)du = L ⎢⎣ t ⎥⎦ , Rep > s1 > s0 p ⎡ sin t ⎤ ⎡ t sin u ⎤ Ví duï 7.12 Tìm: a) L ⎢ b) L ⎢ ∫ du⎥ ⎣ t ⎥⎦ ⎣0 u ⎦ Giaûi 1 ⎡ sin t ⎤ ∞ 1 π a) Ta coù L [sint] = 2 ⇒ L⎢ ⎥ = ∫ 2 du = − arctgp p +1 ⎣ t ⎦ p u +1 2 ⎡ t sin u ⎤ 1 ⎛ π ⎞ b) Theo tính chaát tích phaân haøm goác L ⎢ ∫ du⎥ = ⎜ − arctgp ⎟ ¡ ⎣0 u ⎦ p ⎝2 ⎠ t Ví duï 7.13 Tìm aûnh cuûa haøm goác: f (t ) = u(t − π ) sin(t − π ) + e-3t *sin6t + ∫ e − 2u cos 5udu 0 Giaûi Aùp duïng tính chaát tuyeán tính, tính chaát dòch chuyeån goác, ñònh lyù Borel, tính chaát tích phaân goác
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 13 L [ f (t )] = 1 p +1 2 [ ] e − pπ + L e −3t L [sin 6t ] + 1 p [ L e −2t cos 5t ] 1 1 6 1 p+2 = 2 e − pπ + . 2 + . p +1 p + 3 p + 36 p ( p + 2) 2 + 25 Ví duï 7.14 (Sinh vieân hoaøn thaønh lôøi giaûi ví duï naøy) Tìm aûnh cuûa caùc haøm goác: t a) f(t) = 5 – 3e2t –7 t 2 cost b) f (t ) = t 2 sin 5t + ∫ e − 2u cos 3udu 0 ⎧2 , 0 < t < 2π ⎧ 0 khi 0 < t < π c) f(t) = ⎨ d) Neáu f (t ) = ⎨ vaø f(t+3π) = f(t) ⎩ sin 2t , t > 2π ⎩sin 3t khi π < t < 3π t t e) f (t ) = u (t − 5) sin(3t − 15) + t ∫ e −u cos udu f) f(t) = 5 +sin3t– 3te-2t – t 2 cos2t+ ∫ e − 2u sin 3udu 0 0 Giaûi 1
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 14 §2. TÍCH CHAÄP VAØ AÛNH CUÛA TÍCH CHAÄP 1. Tích chaäp ? Ñònh nghóa Tích chaäp cuûa hai haøm phöùc bieán thöïc f(t) vaø g(t), 0 ≤ t < ∞ ; kyù hieäu laø f * g ñöôïc ñònh nghóa bôûi t t ( f * g )(t ) = ∫ f (u ).g(t − u)du = ∫ g (u ) f (t − u )du = ( g * f )(t ) 0 0 Ñaúng thöùc ôû giöõa trong ba ñaúng thöùc treân coù ñöôïc baèøng caùch ñoåi bieán. Nhö vaäy, tích chaäp coù tính giao hoaùn. Ví duï 7.14 t t2 a) 1*t = ∫ (t − u )du = . 0 2 t b) et*1 = ∫ e u du = et – 1 0 t c) sint*1 = ∫ sin udu = 1-cost 0 t t t d) t*sint = ∫ (t − u ) sin udu = t ∫ sin udu - ∫ u sin udu = t(1-cost) – ( sint – tcost) 0 0 0 = t - sint ¡ ? Caùc tính chaát (i) Giao hoaùn: f ∗ g = g ∗ f (ii) Keát hôïp: (f ∗ g) ∗ h = f ∗ (g ∗ h) = f*g*h (iii) Phaân phoái ñoái vôùi pheùp coäng: f ∗ (g + h) = f ∗ g + f ∗ h (iv) (kf)*g = k(f*g) , vôùi k laø haèng soá. (v) |f ∗ g | ≤ | f | ∗| g | (vi) Neáu f(t) vaø g(t) lieân tuïc trong 0 ≤ t < ∞ thì f ∗ g cuõng lieân tuïc. (vii) Neáu f(t) laø haøm goác vôùi chæ soá taêng s1 vaø g(t) laø haøm goác vôùi chæ soá taêng s2 thì (f ∗ g)(t) laø haøm goác vôùi chæ soá taêng laø max{s1 , s2}. 2 - Aûnh cuûa tích chaäp 2.1 - Ñònh lyù Borel ⎧L [f (t )] = F( p), Re( p) > s 2 ⎫ ⎧L [f * g] = F( p).G( p), Re(p) > max{s1 , s 2 } Neáu ⎨ ⎬ thì ⎨ ⎩L [g(t )] = G( p), Re( p) > s1 ⎭ ⎩ L - 1[F(p).G(p)] = f * g Ví duï 7.15 t a)Tìm aûnh cuûa haøm goác : f(t) = 5 + t sh2t + e-2tcos3t + ∫ e 3u sin(t − u )du . 0
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 15 1 b) Tìm goác cuûa haøm aûnh: F(p) = p ( p 2 + 1) 3 Giaûi a)Aùp duïng tích chaäp ta ñöôïc: f (t ) = 5 + tsh2 t + e −2 t cos 3t + e 3t * sin t Aùp duïng baûng vaø ñònh lyù Borel ta ñöôïc : 5 4P P+2 1 1 L [f (t )] = + + + ⋅ ( ) P P 2 − 4 2 (P + 2 )2 + 9 P − 3 P 2 + 1 b) Aùp duïng baûng vaø ñònh lyù Borel ta ñöôïc : ⎡ 1 ⎤ -1 ⎡ 1 1 1 ⎤ L -1 [F(p)] = L -1 ⎢ 3 2 ⎥ =L ⎢ . 2. 2 ⎥ =1* t * sint = 1*(t*sint) ⎣ p ( p + 1) ⎦ ⎣ p p ( p + 1) ⎦ t2 t2 = 1* (t–sint) = 1*t – 1*sint = - (1- cost) = - 1 + cost ( xem laïi ví duï 7.14) 2 2 ¡ t Ví duï 7.16 Giaûi phöông trình tích phaân sau: y(t) = 2+ ∫ sin(t − u)y(u).du 0 Giaûi Phöông trình töông ñöông vôùi : y(t) = 2 + sint* y(t) Ñaët Y = Y(p) = L [y(t)] bieán ñoåi Laplace hai veá phöông trình vaø aùp duïng coâng thöùc Borel ta ñöôïc 2 2 Y 2( p 2 + 1) 2 2 Y = + L [sint] L [y(t)] ⇔ Y = + 2 ⇔Y= = + 3 p p p +1 p3 p p Bieán ñoåi Laplace ngöôïc hai veá ta ñöôïc : y(t) = L -1[Y] = 2 + t2 ¡ t Ví duï 7.17 Giaûi phöông trình tích phaân: y(t)= e3t+2 ∫ y (u ) cos(t − u )du 0 Giaûi Aùp duïng tích chaäp, phöông trình töông ñöông vôùi: y(t) = e3t +2y(t)*cost Ñaët Y = Y(p) = L [y(t)] bieán ñoåi Laplace hai veá phöông trình ta ñöôïc 1 1 p Y= + 2L [y(t)] L [cost] ⇔ Y = +2Y 2 p−3 p−3 p +1 ( p 2 + 1) (*) A B C Giaûi phöông trình vôùi Y laø aån ta ñöôïc: Y = = + + ( p − 1) ( p − 3) 2 ( p − 1) 2 p −1 p − 3 ( p 2 + 1) (*) A B C Phaân tích thaønh phaân thöùc ñôn giaûn: Y = = + + ( p − 1) ( p − 3) 2 ( p − 1) 2 p −1 p − 3 (vôùi A, B, C = const).
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 16 Bieán ñoåi Laplace ngöôïc hai veá ta ñöôïc nghieäm : y(t) = Ate t + Be t + Ce 3t 32 + 1 12 + 1 Töø ñaúng thöùc (*) tính ñöôïc C = = 5, A = = −1 ; tieáp theo cho p = 0 ñöôïc 3 −1 1− 3 1 C 7 − = A− B− roài theá A, C tính vaøo tính ñöôïc B = − . 3 3 3 2.2 - Coâng thöùc Duhamel Neáu L [f(t)] = F(p), L [g(t)]= G(p) thì L [f(0)g(t) + f’∗ g] = pF(p) G(p). L [g(0)f(t) + f∗ g’] = pF(p) G(p). Ví duï 7.18 pw Aùp duïng coâng thöùc Duhamel tìm goác cuûa haøm H(p) = ( p − α )( p 2 + w 2 ) Giaûi w Ñaët f(t) = sinwt , L [f(t) ] = L [ sinwt ] = , f(0) = 0 , f’(t) = wcowt p2 + w2 1 g(t) = eαt , L [g(t) ] = L [ eαt ] = p−α pw w 1 H(p) = 2 2 = p. 2 2 . = pF(p).G(p) ( p − α)( p + w ) p +w p−α t (t −u) ⇒ L-1[H(p)] = f(0)g(t) + f’∗ g = f’∗ g = w ∫ cos wu.e α du 0 t w sin wt + wα(e αt − cos wt ) 2 = w e α t .∫ cos wu.e -αu du = . ¡ 0 w2 + α2 3- Moät soá caùch tìm haøm goác 3.1 Tìm goác nhôø baûng ñoái chieáu Goác- AÛnh vaø caùc tính chaát cô baûn. Ví duï 7.19 Tìm goác cuûa caùc haøm aûnh p−2 p+8 a) F(p) = 2 b) F(p) = 2 p − 4p − 5 p + 4p + 8 Giaûi p−2 p−2 a) F(p) = 2 = 2 2 ⇒ L -1[F(p)] = e2tch3t. p − 4 p − 5 ( p − 2) − 3 p+8 p+2 2 b) F(p) = 2 = 2 2 + 3. p + 4 p + 8 ( p + 2) + 2 ( p + 2) 2 + 2 2
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 17 ⇒ L -1[F(p)]= e-2tcos2t + 3e-2tcos2t ¡ 3.2-Tìm goác nhôø ñònh lyù Borel vaø coâng thöùc Duhamel Neáu bieát L [f(t)]= F(p) vaø L [g(t)]= G(p) thì coù theå tìm goác cuûa F(p)G(p), pF(p)G(p) nhôø tích chaäp. ⎡ 1 ⎤ -1 ⎡ 1 ⎤ -1 ⎡ 1 ⎤ Ví duï 7.20 L -1 ⎢ 2 ⎥= L ⎢ 2⎥ L ⎢ ⎥ = t * et = et-t – 1 ¡ ⎣ p ( p − 1) ⎦ ⎣p ⎦ ⎣ p − 1⎦ 3.3-Tìm goác nhôø khai trieån thaønh phaân thöùc ñôn giaûn Ví duï 7.21 (Sinh vieân hoaøn thaønh lôøi giaûi ví duï naøy) Tìm goác cuûa caùc haøm aûnh sau : p2 + 2p + 3 4 p 3 − 3 p 2 + 10 p − 16 a) F(p) = b) F(p) = ( p 2 + 2 p + 2)( p 2 + 2 p + 5) ( p − 1)( p − 2)( p 2 + 4) 2p2 − 4 p3 + 2 p + 3 p +1 c) F(p) = d) F(p) = + 2 ( p + 1)( p − 2)( p − 3) ( p − 2) ( p + 1)( p − 4 p + 13) ( p − 4 p + 29)( p − 1) 3 2 Giaûi 2
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 18
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 19 BIEÁN ÑOÅI LAPLACE – TÍNH CHAÁT Coâng thöùc Teân – Tính chaát +∞ Ñònh nghóa bieán ñoåi laplace F(p) = L [f(t)]= ∫ e f (t )dt − pt 0 bieán ñoåi laplace ngöôïc f(t) = L -1[F(P)] L [αf(t) +β g(t)] = α L [f(t)]+β L [g(t)] Tính chaát tuyeán tính L [eat f(t)] = F(p-a) L -1[F(p-a)]= eat f(t) Tính chaát dòch chuyeån aûnh L [u(t-a) f(t-a)] = e-ap F(p) L -1[ e-ap F(p)] = u(t-a) f(t-a) Tính chaát dòch chuyeån goác L [f’(t)] = p L [f(t)]-f(0) L [f’’(t)] = p2 L [f(t)]-pf(0)-f’(0) M Tính chaát ñaïo haøm haøm goác L [f (t)] = p L [f(t)]-pn-1f(0)-……-f(n-1)(0) (n) n ⎡t ⎤ 1 L ⎢ ∫ f (u)du ⎥ = L [f(t)] Tính chaát tích phaân haøm goác ⎢0 ⎥ p ⎣ ⎦ Aûnh cuûa haøm goác tuaàn hoaøn T 1 − pt f ( t ) dt L [f(t)] = ∫e 1 − e− Tp 0 chu kyø T L [t f(t)] = -F’(p) , L [t2f(t)]= F’’(p)….... Tính chaát ñaïo haøm haøm aûnh ….L [tnf(t)]= (-1)n F(n)(p) ( nhaân t) ⎡ f (t ) ⎤ ∞ Tính chaát tích phaân haøm aûnh L⎢ = ∫ F(u)du (chia t) ⎣ t ⎥⎦ p t t Tích chaäp- Aûnh cuûa tích chaäp (f*g)(t) = ∫ f (u ).g(t − u)du = ∫ f (t − u ).g(u)du 0 Ñònh lyù Borel 0 L [f*g] = L [ f(t)] L [ g(t)] L [f(0)g(t) + f’∗ g] = pF(p) G(p) Coâng thöùc Duhamel L [g(0)f(t) + f∗ g’] = pF(p) G(p)
Pheùp bieán ñoåi Laplace.........……………………………………………….......................................................Trang 20 BAÛNG ÑOÁI CHIEÁU GOÁC - AÛNH CÔ BAÛN STT f(t) F(p) = L[f(t)] STT f(t) F(p) = L [f(t)] 01 1 1 11 αt p −α e chwt p ( p − α ) 2 − w2 02 t 1 t eα 12 eα shwt w p −α ( p − α ) 2 − w2 n 13 tsinwt 2 pw 03 t n! p n +1 ( p + w2 ) 2 2 tcoswt p2 − w2 04 sinwt w 14 p + w2 2 ( p2 + w2 )2 p 15 tshwt 2 pw 05 coswt p + w2 2 ( p − w2 ) 2 2 t n! 16 tchwt p2 + w2 06 tn eα ( p − α ) n +1 ( p2 − w2 )2 w 17 e at − e bt 1 07 shwt p − w2 2 a −b ( p − a)( p − b) p 08 chwt 18 e at − e bt p−b p2 − w2 ln t p−a t w 2 w( p − α ) 09 eα sinwt 19 t ( p − a) 2 + w 2 t eα sinwt [( p − α ) ] 2 2 + w2 10 t p −α ( p − α)2 − w2 eα coswt t ( p − α )2 + w2 20 t eα coswt [( p − α ) 2 + w2 ] 2