CH NG 19ƯƠ
Bây gi chúng ta ờcó đ thông tin vủ ề s li uố ệ không gian đ xem xétể m t s ng d ngộ ố ứ ụ thú vị.
Chúng tôi đ u tiên sầ ẽ ch ngứ minh m t k t quộ ế ả đ cượ g iọ là đ nh lýị l p ậánh x coạ và sau đó sử
d ngụ nó đ tìmể gi i phápả cho các h th ngệ ố ph ng trìnhươ tuy n tínhế và ph ngươ trình tích phân
xác đ nhị. K ểtừ khi ch ng nàyươ ch a ch y u làứ ủ ế ví dụ, chúng ta sẽ làm cho vi c s d ngệ ử ụ t doự
c aủ tính toán t đ uừ ầ tính toán. M c dù nó ặcó lẽ s làẽ h p lý đợ ể trì hoãn các v n đ nàyấ ề cho đ nế
khi chúng ta đã phát tri nể các s ki nự ệ c nầ thi tế liên quan đ nế tích phân, các đ o hàm ạvà lũy
th aừ, tuy nhiên nhi u đi u đ nóiề ề ể cho trình bày m t s ng d ngộ ố ứ ụ không t m th ngầ ườ t ng đ iươ ố
s mớ.
19.1. Đ NH LÝ ÁNH X COỊ Ạ
19.1.1. Đ nh nghĩaị.
M tộ ánh xạ f: M → N gi aữ không gian metric là co n uế có t n t i m t ồ ạ ộ đi m ểc liên t cụ mà
0 <c <1 và d (f (x), f (y)) ≤ cd (x, y) v iớ x, y ∈ M. Số c là co liên t cụ cho f. M t ánh x ộ ạ cũng
đ c g i ươ ọ là đ c ượ g iọ là sự co.
19.1.2. Bài t p:ậ Ch ng minh r ng t tứ ằ ấ c các ảánh x co ạliên t c. (ụQ.19.1.)
19.1.3. Ví d :ụ
Cho ánh x ạf :
2 3
R R
xác đ nh b i ị ở
1 1 1 1
( , ) (1 ,1 ,2 )
3 3 3 3
f x y x y x y= − + + −
là co.
Ch ng minh: (ứQ.19.2)
19.1.4. Ví d .ụ Ánh x ạ
2 2
1 1
: : ( , ) ( (1 ), (3 ))
2 2
f R R x y y x + −a
là m t ánh x co trên ộ ạ
2 2
,R R
có không gian metric th ng.ườ
CH NG MINH. V n đ . Ứ ấ ề
Đ nh lý ịti p theo làế c s choơ ở m t sộ ố ng d ng thú vứ ụ ị. Ngoài ra, nó sẽ b t raậ là m t ộthành
ph nầ quan tr ng c aọ ủ đ nh lýị hàm ng c ượ r t quan tr ng (ấ ọ trong ch ng ươ 29). M c dùặ tuyên bố c aủ
đ nh lýị 19.1.5 là quan tr ngọ trong các ng d ngứ ụ , b ng ch ngằ ứ c a nóủ th m chí cònậ h n th n aơ ế ữ .
Đ nh lý này ịđ m b oả ả s t n t iự ồ ạ và tính đ c đáoộ c a các gi i phápủ ả cho m t s lo iộ ố ạ ph ngươ
trình; b ng ch ng ằ ứ cho phép chúng tôi tính x p x nh ngấ ỉ ữ gi i phápả như ch t chặ ẽ c a chúng tôiủ
cho phép máy móc thi t bế ị tính toán. Nh l i ớ ạ t ch ngừ ươ 5 là m t đi m c đ nhộ ể ố ị c a m tủ ộ f ánh xạ
từ m tộ t p h pậ ợ S vào chính nó là m tộ đi mể p
S nh v y mà ư ậ f (p) = p.
19.1.5.Đ nh lýị (Ánh x coạ). M iỗ ánh x ạco t m từ ộ không gian metric đ y đầ ủ vào chính nó có
m t đi m duy nh tộ ể ấ c đ nhố ị .
Ch ng minhứ. G i ýợ. M là m tộ không gian metric đ y đầ ủ và f:M
M là co.
B t ắđ uầ v i m tớ ộ
0
x
đi mể tùy ý trong M. Có đ cượ m t chu iộ ỗ (
n
x
) trong M b ng cách choằ
1 0 2 1
( ), ( ),...x f x x f x= =
Cho th yấ trình tự này là Cauchy. (Đáp án Q.19.3.)
19.1.6. Ví dụ.
Chúng ta s d ng ử ụ đ nh lýị Ánh x coạ đ gi i quy tể ả ế các hệ ph ng trìnhươ sau đây:
(19.1)
Xác đ nhị
.
H ệph ng trìnhươ (19.1) có th đ c vi tể ượ ế nh là m tư ộ ph ngươ trình duy nh tấ S(x, y) = (7, 11)
ho c t ng đ ng nhặ ươ ươ : ư
(x, y) - S (x, y) + (7, 11) = (x, y). (19,2)
Đ nh nghĩaị. C ng và tr vào R2 đ c đ nh nghĩa coordinatewise. Đó là, n u (x, y) và (u, v)ộ ừ ượ ị ế
là đi m ể, sau đó (x, y) + (u, v) = (x + u, y + v) và (x, y) - (u, v) = (x - u, y - v ). T ng tươ ự đ nhị
nghĩa t p b ch nậ ị ặ cho v i n> 2]ớ. Đ tặ T (x, y) là phía bên tay trái ở(19,2). Ta đ cượ :
T: → : (x, y) → (x, y) - S (x, y) + (7, 11).
V i ớký hi uệ này (19,2) tr thànhở: T (x, y) = (x, y).
Nh v yư ậ , và đây là đi mể r t quan tr ng,ấ ọ đ gi i quy tể ả ế (19.1), chúng ta ch c nỉ ầ tìm th yấ m tộ
đi m c đ nhể ố ị c aủ ánh x ạT. N u T lếà co, thì đ nh lýị tr cướ đó đ m ảb o Tả có m t đi m duy nh tộ ể ấ
c đ nhố ị và do đó h ph ng trìnhệ ươ (19.1) có m t ộph ng ươ pháp gi iả duy nh tấ.
Th t ậti cế, nh ng ữquan đi m đóể, T không ph i làả co đ iố v iớ các không gian metric tích trên
. (Cho thu n ti n ậ ệ mà chúng ta s d ngử ụ không gian metric tích trên h nơ là Euclide thông
th ngườ căn b c haiậ quả là m t m i phi n toáiộ ố ề .) Th y r ngấ ằ T không ph iả là co chú ý r ngằ
((1, 0), (0, 0)) = 1 trong khi (T (1, 0), T (0, 0)) = ((-1, 8), (7, 11)) = 11. T t c là khôngấ ả bị
m tấ băng bât c cach nao% & ư& & % . M tộ bi n pháp kh c ph cệ ắ ụ đ n gi nơ ả là chia t t c m i th trongấ ả ọ ứ
(19.1) b i ởc l n tùy ýớ. M tộ th nghi mử ệ nhỏ cho th yấ r ngằ c = 10. Thay vì làm vi c v iệ ớ hệ
(19.1), hãy xem xét hệ: (19.3)
mà rõ ràng là có các ph ngươ pháp t ng t nh ươ ự ư (19.1). Xác đ nh l i S và T ị ạ d ng c th : ở ạ ụ ể
Đ t ặS: → : (x, y) → (0.9x - 0.2y, 0.3x + 0.8y)
và T: → : (x, y) → (x, y) - S (x, y) + (0.7, 1.1). Vì v y đ nh nghĩa l i, T ậ ị ạ co đ i v i ố ớ không
gian metric tích.
C h ngứ minh : Từ T (x, y) = (0.1x + 0.2y + 0,7-0.3x + 0.2y + 1,1) (19,4)
V iớ (x, y) , chúng ta th y r ng ấ ằ
d(T (x, y) ,T (u, v)) = (|(x + 2y) - (u + 2v) | + | (-3x + 2y) - (-3u + 2v) |)
≤ (| x - u | + 2 | y - v | + 3 | x - u | + 2 | y - v |)
= 0.4 (| x - u | + | y - v |)
= 0.4 ((x, y), (u, v)) (19,5)
V iớ t t c các đi m (x, y) và (u, v) ấ ả ể thu c ộ .
Bây giờ t T là ừco và là đ y đ (đ i v i ầ ủ ố ớ không gian metric tích xem 18.2.9), các đ nh lýị
ánh x coạ (19.1.5) cho chúng ta bi t r ng T có m t đi m duy nh t c đ nh. Nh ng m t đi m cế ằ ộ ể ấ ố ị ư ộ ể ố
đ nh c a T là m t gi i pháp cho h ị ủ ộ ả ệ (19,3) và cho (19.1).
Bài toán đ c s d ng trongượ ử ụ các ch ngứ minh c aủ 19.1.5 cho phép chúng tôi tính g n đúngầ
đi mể cố đ nhị c aủ T đ ểmong mu n ốb t kỳ m c đấ ứ ộ chính xác. Trong ch ng minhứ đó ch nọ là
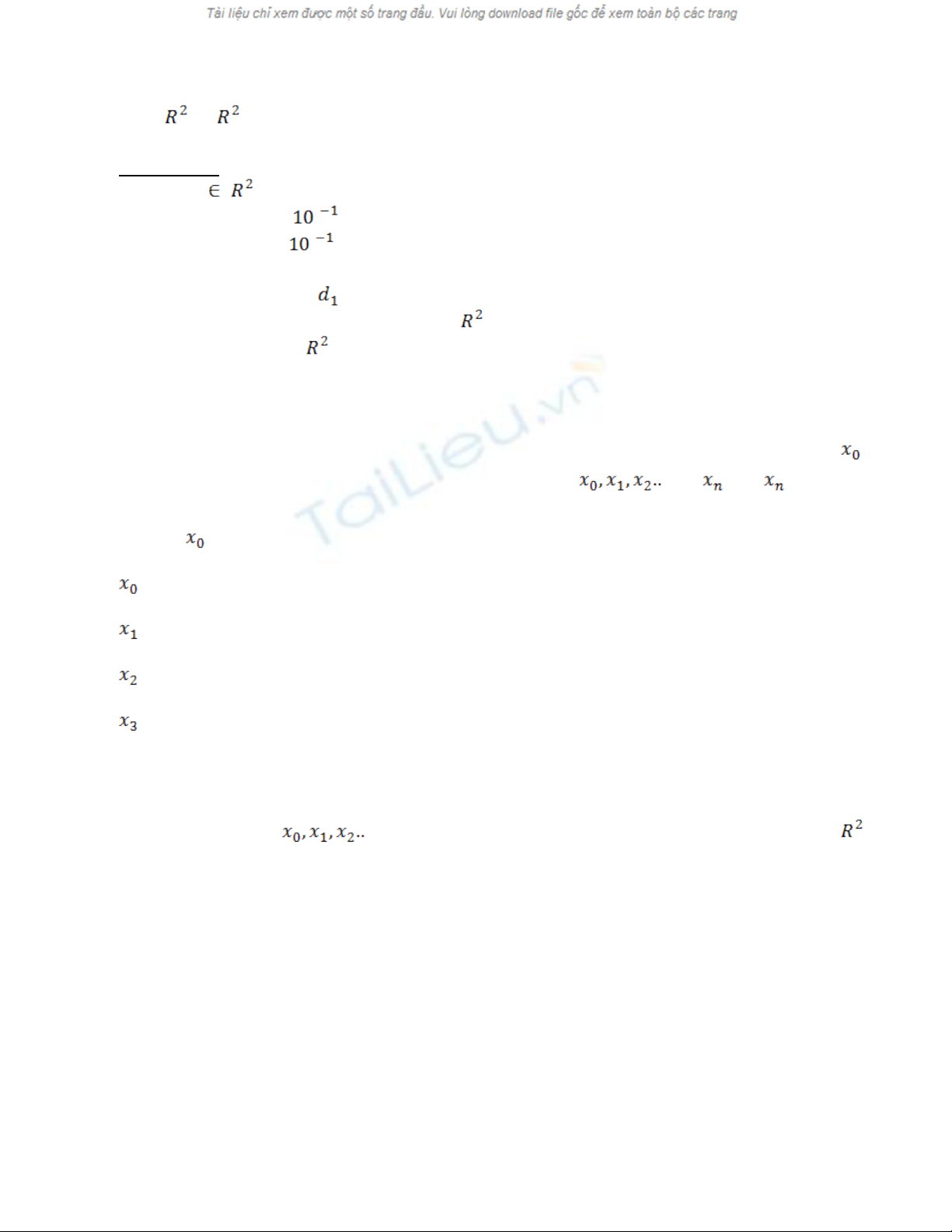
b t kỳ đi m nàoấ ể b tấ cứ đi uề gì trong R2. Sau đó, các đi mể ,. . . ( = T( -1) cho m iỗ
n) h i t vộ ụ ề các đi m c đ nhể ố ị c aủ T. Đây là m tộ k thu tỹ ậ đ tínhẻ x p xấ ỉ liên ti pế. Đ i v i víố ớ
dụ này cho = (0, 0). (G c ốđ c ch nượ ọ cho thu n ti n.ậ ệ ) Bây gi ờs d ngử ụ (19,4) và tính toán.
= (0, 0)
= T(0, 0) = (0.7, 1.1)
= T(x1) = (1.021, 1.025)
= T(x2) = (1.0071, 0.9987)
…………..
Nó là c sơ ở ph ng đoán r ng h ỏ ằ ệ (19.1) có m t gi i pháp bao g m các con s h p lý và sauộ ả ồ ố ợ
đó đoán r ng các đi mằ ể . nh tính toán trên đang h i t đ các đi m (1, 1) trong ư ở ộ ụ ể ể .
Trong (19,4), Đ t x = 1 và y = 1 chúng ta th y r ng các đi m (1, 1) th c s là đi m c đ nhặ ấ ằ ể ự ự ể ố ị
c a T và do đó gi i ủ ả quy tế đ c ượ (19.1).
Trong ví d trên, chúng tôi phát hi n ra m t gi i pháp chính xác m t h ph ng trình. Nóiụ ệ ộ ả ộ ệ ươ
chung, t t nhiên, chúng ta không th hy v ng r ng m t k thu t x p x k ti p s mang l i câuấ ể ọ ằ ộ ỹ ậ ấ ỉ ế ế ẽ ạ
tr l iả ờ chính xác. Trong nh ng tr ng h p khôngữ ườ ợ chính xác, nó là quan tr ng nh t đ có m t sọ ấ ể ộ ố
ý t ng làm th nào chính xác ưở ế v i ớx p x c a chúng tôi. Sau khi l p đi l p l i nấ ỉ ủ ặ ặ ạ l nầ, làm th nàoế
l y k t qu ấ ế ả g n ầđúng v i các gi i pháp th c s ? ớ ả ự ự Bao nhiêu l n l p l i pầặạhép toán đ đ t đ cể ạ ượ
m t m c đ mong mu n chính xác? Câu tr l i cho nh ng câu h i trong m t h qu d dàngộ ứ ộ ố ả ờ ữ ỏ ộ ệ ả ễ
ch ng minh đ nh lý 19.1.5.ứ ị
19.1.7.H ệquả.