1
Đề số 4
ĐỀ THI THỬ HỌC KÌ 2 – Năm học 2010 – 2011
Môn TOÁN Lớp 11
Thời gian làm bài 90 phút
I. Phần chung: (7,0 điểm)
Câu 1: (2,0 điểm) Tìm các giới hạn sau:
a) x
x x
x
2
3
1
3 2 1
lim
1
b) x
x
x
3
3
lim
3
Câu 2: (1,0 điểm) Xét tính liên tục của hàm số sau tại điểm x0
2
:
x x khi x
x
f x
khi x
2
2 3 2
2 4
( ) 3
2
2
Câu 3: (1,0 điểm) Tính đạo hàm của các hàm số sau:
a) x
yx
2 3
2
b)
y x
2
(1 cot )
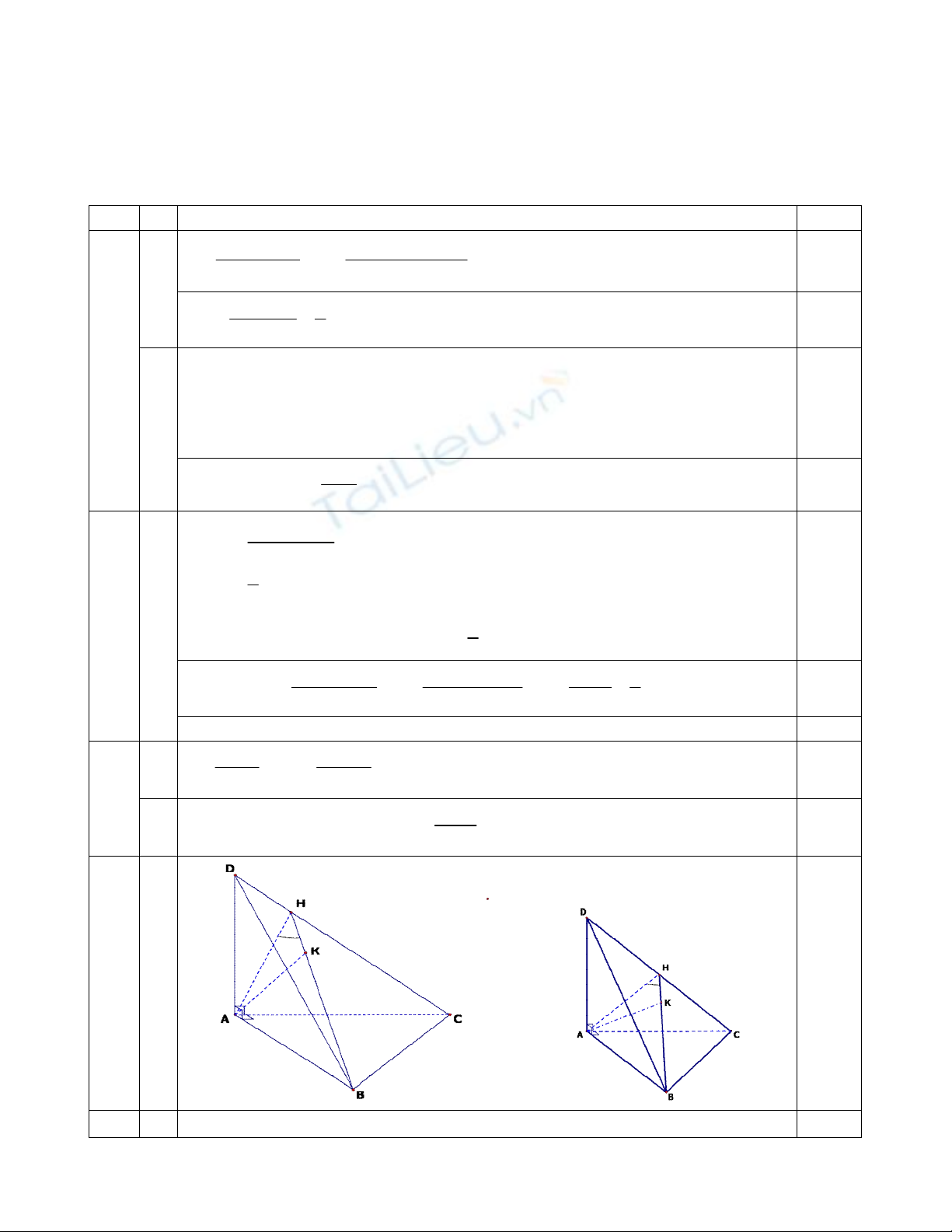
Câu 4: (3,0 điểm) Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau. Gọi H là chân đường cao
vẽ từ A của tam giác ACD.
a) Chứng minh: CD BH.
b) Gọi K là chân đường cao vẽ từ A của tam giác ABH. Chứng minh AK (BCD).
c) Cho AB = AC = AD = a. Tính cosin của góc giữa (BCD) và (ACD).
II. Phần riêng
1. Theo chương trình Chuẩn
Câu 5a: (1,0 điểm) Chứng minh rằng phương trình sau có ít nhất một nghiệm:
x x
2
cos 0
Câu 6a: (2,0 điểm) Cho hàm số y f x x x x
3 2
( ) 3 9 2011
có đồ thị (C).
a) Giải bất phương trình: f x
( ) 0
.
b) Viết phương trình tiếp tuyến với đồ thị (C) tại điểm có hoành độ bằng 1.
2. Theo chương trình Nâng cao
Câu 5b: (1,0 điểm) Chứng minh rằng phương trình sau có ít nhất hai nghiệm nằm trong khoảng
( 1; 2)
:
m x x
2 2 3
( 1) 1 0
Câu 6b: (2,0 điểm) Cho hàm số
x x
yx
2
2 1
1
có đồ thị (C).
a) Giải phương trình: y
0
.
b) Viết phương trình tiếp tuyến với đồ thị (C) tại giao điểm của (C) với trục tung.
--------------------Hết-------------------
2
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ II – NĂM HỌC 2010 – 2011
MÔN TOÁN LỚP 11 – ĐỀ SỐ 4
Câu Ý Nội dung Điểm
x x
x x x x
x x x x
2
3 2
1 1
3 2 1 ( 1)(3 1)
lim lim
1 ( 1)( 1)
0,50
a)
x
x
x x
2
1
3 1 4
lim
3
1
0,50
Viết được ba ý
x
x
x
x x
x
3
3
lim( 3) 0
3 3 0
lim( 3) 6 0
0,75
1
b)
Kết luận được x
x
x
3
3
lim 3

0,25
x x khi x
x
f x
khi x
2
2 3 2
2 4
( ) 3
2
2
Tập xác định D = R. Tính được f(2) =
3
2
0,25
x x
x x
f x x
2
2 2
2 3 2
lim ( ) lim
2 4
x
x x
x
2
( 2)(2 1)
lim
2( 2)
x
x
2
2 1 5
lim
2 2
0,50
2
Kết luận hàm số không liên tục tại x = 2. 0,25
a) x
yx
2 3
2
yx
2
1
'
( 2)
0,50
3
b)
y x
2
(1 cot )
y x x x
x2
2
1
2(1 cot ) 2(1 cot )(1 cot )
sin
0,50
4 a)
0,25
a) AB AC, AB AD AB (ACD) AB CD (1) 0,25
3
AH CD (2). Từ (1) và (2) CD (AHB) CD BH 0,50
AK BH, AK CD (do CD (AHB) (cmt) 0,50
b)
AK (BCD) 0,50
Ta có AH CD, BH CD
BCD ACD AHB
( ),( ) 0,25
Khi AB = AC = AD = a thì AH =
2
2 2
CD a
0,25
BH = a a
AB AH a 2
2 2 2
6
2 2
0,25
c)
AH
AHB BH
1
cos
3
0,25
Đặt f(x) = 2
cos
x x
f(x) liên tục trên
(0; )

f(x) liên tục trên
0;
2
0,25
f f f f
(0) 1, (0). 0
2 2 2
0,50
5a
Vậy phương trình có ít nhất một nghiệm trên
0;
2
0,25
y f x x x x
3 2
( ) 3 9 2011
f x x x
2
( ) 3 6 9
0,25
BPT f x x x
2
( ) 0 3 6 9 0
0,25
a)
x
x
3
1
0,50
0 0
1 2016
x y , f
(1) 0
0,50
6a
b)
Vậy phương trình tiếp tuyến là y = 2016 0,50
Đặt f(x) = 2 2 3
( 1) 1
m x x
f(x) liên tục trên R nên liên tục trên
[ 1; 2]
0,25
f m f f f m R
2
( 1) 1, (0) 1 ( 1). (0) 0,
0,50
5b
phương trình có ít nhất một nghiệm thuộc
( 1;0) 1; 2
(đpcm) 0,25
2
2 1
1
x x
yx
, TXĐ : D = R\{1}, x x
yx
2
2
2 4 2
'
( 1)
0,50
a)
Phương trình y’ = 0 2 2
1 2
2 4 2 0 2 1 0
1 2
x
x x x x x
0,50
Giao của ( C) với Oy là A(0; –1) 0,25
x y k f
0 0
0, 1, (0) 2
0,20
6b
b)
Phương trình tiếp tuyến cần tìm là
y x
2 1
0,50