TRƯỜNG THPT LƯƠNG THẾ VINH KỲ THI TỐT NGHIỆP THPT
ĐỀ THI THỬ TỐT NGHIỆP Môn thi: TOÁN − Giáo dục trung học phổ thông
Đề số 1 Thời gian làm bài: 150 phút, không kể thời gian giao đề
------------------------------ ---------------------------------------------------
I. PHẦN CHUNG DÀNH CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)
Câu I (3,0 điểm): Cho hàm số: 32
( ) 2 3
3
x
y f x x x
= = - + -
1) Khảo sát sự biến thiên và vẽ đồ thị
( )
C
của hàm số.
2) Viết phương trình tiếp tuyến của
( )
C
tại điểm trên
( )
C
có hoành độ
0
x
, với
0
( ) 6
f x
¢¢
.
3) Tìm tham số m để phương trình 3 2
6 9 3 0
x x x m
- + + =
có đúng 2 nghiệm phân
biệt.
Câu II (3,0 điểm):
1) Giải phương trình: 4 4 2 4
2 17.2 1 0
x x- -
- + =
2) Tính tích phân: 0(2 1)sin
I x xdx
p
= -
ò
3) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
4ln(1 )
y x x
= - -
trên đoạn [– 2;0]
Câu III (1,0 điểm):
Cho hình lăng trụ đứng
.
A BC A B C
¢ ¢ ¢
có đáy ABC là tam giác vuông tại B, BC = a, mặt
( )
A BC
¢ tạo với đáy một góc
0
30
và tam giác
A BC
¢
có diện tích bằng 2
3
a. Tính thể
tích khối lăng trụ
.
A BC A B C
¢ ¢ ¢
.
II. PHẦN RIÊNG (3,0 điểm) Thí sinh chỉ được chọn một trong hai phần dưới đây
1. Theo chương trình chuẩn
Câu IVa (2,0 điểm): Trong không gian với hệ toạ độ Oxyz, cho hai điểm
(7;2;1), ( 5; 4; 3)
A B
- - -
và mặt phẳng
( ) : 3 2 6 38 0
P x y z
- - + =
1) Viết phương trình tham số của đường thẳng AB. Chứng minh rằng, AB ||
( )
P
.
2) Viết phương trình mặt cầu
( )
S
có đường kính AB.
3) Chứng minh
( )
P
là tiếp diện của mặt cầu
( )
S
. Tìm toạ độ tiếp điểm của
( )
P
và
( )
S
Câu Va (1,0 điểm): Cho số phức
1 3
z i
= + . Tìm số nghịch đảo của số phức: 2
.
z z z
w= +
2. Theo chương trình nâng cao
Câu IVb (2,0 điểm): Trong không gian với hệ toạ độ Oxyz, cho cho điểm
(1;3; 2)
I
-
và đường
thẳng
4 4 3
:
1 2 1
x y z
- - +
D = =
-
1) Viết phương trình mặt phẳng (P) đi qua điểm I và chứa đường thẳng
D
.
2) Tính khoảng cách từ điểm I đến đường thẳng
D
.
3) Viết phương trình mặt cầu (S) có tâm là điểm I và cắt
D
tại hai điểm phân biệt A,B
sao cho đoạn thẳng AB có độ dài bằng 4.
Câu Vb (1,0 điểm): Gọi
1 2
,
z z
là hai nghiệm của phương trình: 2
2 2 2 2 0
z z i
- + + =
. Hãy
lập một phương trình bậc hai nhận
1 2
,
z z
làm nghiệm.
---------- Hết ----------
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh: ........................................ Số báo danh:
...............................................
Chữ ký của giám thị 1: .................................. Chữ ký của giám thị 2:
.................................
x
y
y = m
-2/ 3
4
-4/ 3
3
2
O1
BÀI GIẢI CHI TIẾT.
Câu I:
Hàm số: 32
( ) 2 3
3
x
y f x x x
= = - + -
Tập xác định:
D
=
¡
Đạo hàm: 2
4 3
y x x
¢
= - + -
Cho 2
0 4 3 1; 3
y x x x x
¢
= Û - + - Û = =
Giới hạn: ; lim lim
x x
y y
® - ¥ ® + ¥
= + ¥ = - ¥
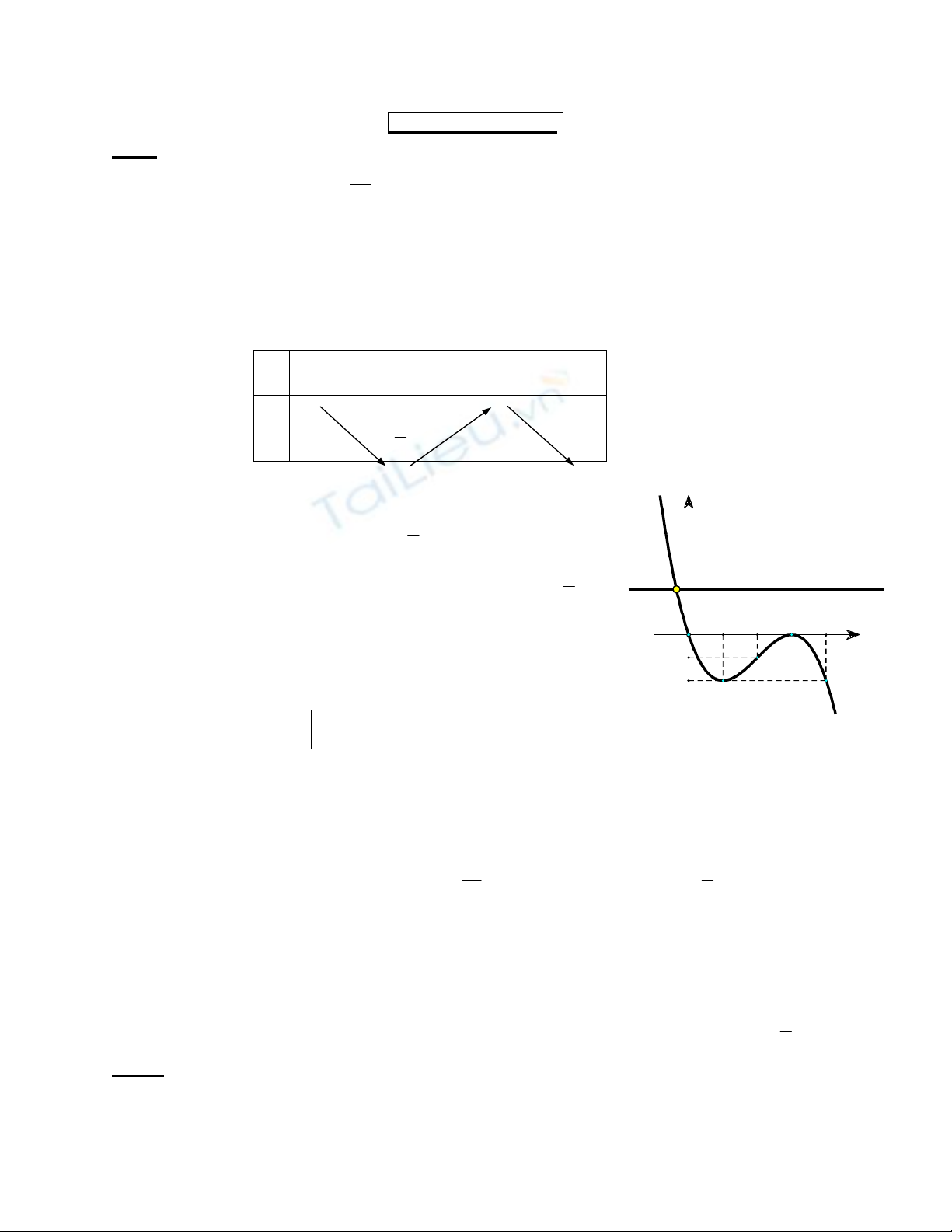
Bảng biến thiên
x –
1 3 +
y
¢
– 0 + 0 –
y
+
0
4
3
-
–
Hàm số ĐB trên khoảng (1;3), NB trên các khoảng (–;1), (3;+)
Hàm số đạt cực đại CÑ
0
y
=
tại CÑ
3
x
=
,
đạt cực tiểu CT
4
3
y
= -
tại CT
1
x
=
Điểm uốn:
2
2 4 0 2
3
y x x y
¢¢
= - + = Û = Þ = -
.
Điểm uốn của đồ thị là:
2
2;
3
I
æ ö
÷
ç
÷
-
ç
÷
ç
è ø
Giao điểm với trục hoành: cho
0 0; 3
y x x
= Û = =
Giao điểm với trục tung: cho
0 0
x y
= Þ =
Bảng giá trị: x 0 1 2 3 4
y 0 –4/3 –2/3 0 –4/3
Đồ thị hàm số như hình vẽ:
0 0 0 0
16
( ) 6 2 4 6 1
3
f x x x y
¢¢ = Û - + = Û = - Þ =
2
0
( ) ( 1) ( 1) 4( 1) 3 8
f x f
¢ ¢
= - = - - + - - = -
Phương trình tiếp tuyến cần tìm:
16 8
8( 1) 8
3 3
y x y x
- = - + Û = - -
3 2 3 2 3 2
1
6 9 3 0 6 9 3 2 3
3
x x x m x x x m x x x m
- + + = Û - + = - Û - + - = (*)
Số nghiệm phương trình (*) bằng số giao điểm của
( )
C
và :
d y m
=
Dựa vào đồ thị ta thấy phương trình (*) có đúng 2 nghiệm phân biệt
0
4
3
m
m
é=
ê
ê
Ûê
= -
ê
ë
Câu II:
30 a
B'
C'
AC
B
A'
4 4 2 4 2
16 4
2 17.2 1 0 17. 1 0 4 17.4 16 0
16 16
x x
x x x x- -
- + = Û - + = Û - + =
(*)
Đặt
4
x
t
=
(ĐK: t > 0) phương trình (*) trở thành
(nhan)
(nhan)
2
1 4 1 0
17 16 0
16 2
4 16
x
x
t x
t t t x
é
é é
= = =
ê
ê ê
- + = Û Û Û
ê
ê ê
= =
=
ê
ê ê
ë ë
ë
Vậy, phương trình đã cho có hai nghiệm: x = 0 và x = 2.
0(2 1)sin
I x xdx
p
= -
ò
Đặt
2 1 2.
sin cos
u x dx dx
dv xdx v x
ì ì
ï ï
= - =
ï ï
Þ
í í
ï ï
= = -
ï ï
î î
. Thay vào công thức tích phân từng phần ta được:
0
00
(2 1)cos ( 2cos ) (2 1) 1 2sin (2 1) 1 2.0 2 2
I x x x dx x
p
p p
p p p
= - - - - = - - + = - - + = -
ò
Hàm số 2
4ln(1 )
y x x
= - -
liên tục trên đoạn [–2;0]
2
4 2 2 4
2
1 1
x x
y x
x x
- + +
¢= + =
- -
Cho
(nhan)
(loai)
21 [ 2;0]
0 2 2 4 0 2 [ 2;0]
x
y x x
x
é= - Î -
ê
¢= Û - + + = Û ê= Ï -
ê
ë
; ;
( 1) 1 4ln 2 ( 2) 4 4 ln 3 (0) 0
f f f
- = - - = - =
Trong các kết quả trên, số nhỏ nhất là:
1 4 ln 2
-
, số lớn nhất nhất là: 0
Vậy, khi
[ 2;0] [ 2;0]
min 1 4 ln 2 1 ; max 0
y x y
- -
= - = - =
khi x = 0
Câu III
Do
BC A B
BC A B
BC A A
ì
ï^
ï
¢
Þ ^
í¢
ï^
ï
î
(hơn nữa,
( )
BC ABB A
¢ ¢
^)
Và
·
( )
( )
( ) ( )
BC A B ABC
BC A B A BC A BA
BC ABC A BC
ì
ï^ Ì
ï
ï
ï
¢ ¢
^ Ì Þ
í
ï
ï¢
= Ç
ï
ï
î
là góc giữa
( )
ABC
và
( )
A BC
¢
Ta có, 2
2.
1 2. 3
. 2 3
2
A BC
A BC
Sa
S A B BC A B a
BC a
¢
D
¢
D¢ ¢
= Þ = = =
·
·
0
0
.cos 2 3.cos30 3
.sin 2 3.sin 30 3
AB A B ABA a a
AA A B ABA a a
¢ ¢
= = =
¢ ¢ ¢
= = =
Vậy, l.truï
3
1 1 3 3
. . 3 3
2 2 2
ABC
a
V B h S AA AB BC AA a a a
¢ ¢
= = = × × × = × × × = (đvtt)
THEO CHƯƠNG TRÌNH CHUẨN
Câu IVa:
(7;2;1), ( 5; 4; 3)
A B
- - -
Đường thẳng AB đi qua điểm
(7;2;1)
A, có vtcp
( 12; 6; 4)
u AB
= = - - -
uuur
r
nên có ptts
7 12
: 2 6
1 4
x t
AB y t
z t
ì
ï= -
ï
ï
ï= -
í
ï
ï= -
ï
ï
î
(1)
Thay (1) vào phương trình mp(P) ta được:
3(7 12 ) 2(2 6 ) 6(1 4 ) 38 0 0. 49 0 0 49
t t t t t
- - - - - + = Û + = Û = -
: vô lý
Vậy,
|| ( )
AB P
Tâm của mặt cầu
( )
S
:
(1; 1; 1)
I
- -
(là trung điểm đoạn thẳng AB)
Bán kính của
( )
S
: 2 2 2
(1 7) ( 1 2) ( 1 1) 7
R IA
= = - + - - + - - =
Phương trình mc 2 2 2
( ) : ( 1) ( 1) ( 1) 49
S x y z- + + + + =
Ta có, 2 2 2
3.1 2.( 1) 6.( 1) 38
( ,( )) 7
3 ( 2) ( 6)
d I P R
- - - - +
= = = Þ
+ - + -
( )
P
tiếp xúc với
( )
S
.
Gọi d là đường thẳng đi qua điểm I và vuông góc với mp(P).
Khi đó PTTS của d:
1 3
1 2
1 6
x t
y t
z t
ì
ï= +
ï
ï
ï
= - -
í
ï
ï
= - -
ï
ï
î
. Thay vào ptmp(P) ta được :
3(1 3 ) 2( 1 2 ) 6( 1 6 ) 38 0 49. 49 0 1
t t t t t
+ - - - - - - + = Û + = Û = -
Tiếp điểm cần tìm là giao điểm của d và (P), đó là điểm
( 2;1;5)
H-
Câu Va: Với
1 3
z i
= + , ta có
2 2 2 2 2
. (1 3 ) (1 3 )(1 3 ) 1 6 9 1 9 2 6
z z z i i i i i i i
w
= + = + + + - = + + + - = +
2 2
1 1 2 6 2 6 2 6 1 3
2 6 (2 6 )(2 6 ) 40 10 10
2 36
i i i
i
i i i i
w
- - -
= = = = = -
+ + - -
THEO CHƯƠNG TRÌNH NÂNG CAO
Câu IVb:
Đường thẳng
D
đi qua điểm
(4;4; 3)
M
-
, có vtcp
(1;2; 1)
u
= -
r
Mặt phẳng
( )
P
đi qua điểm
(1;3; 2)
I
-
Hai véctơ:
(3;1; 1)
IM
= -
uuur
(1;2; 1)
u
= -
r
Vtpt của mp(P): 1 1 1 3 3 1
[ , ] ; ; (1;2;5)
2 1 1 1 1 2
n IM u æ ö
- - ÷
ç÷
ç
= = =
÷
ç÷
ç- - ÷
÷
ç
è ø
uuur
r r
PTTQ của mp
( ) : 1( 1) 2( 3) 5( 2) 0
P x y z
- + - + + =
2 5 3 0
xyz
Û + + + =