Đề thi thứ tốt nghiệp THPT Toán - THPT Phan Châu Trinh (2013-2014)

Chia sẻ: Lê Thị Hoa | Ngày: | Loại File: PDF | Số trang:5

Thêm vào BST

Báo xấu

46
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tài liệu tham khảo đề thi thứ tốt nghiệp THPT Toán - THPT Phan Châu Trinh (2013-2014) giúp các bạn học sinh có thêm tư liệu ôn tập, luyện tập để nắm vững được những kiến thức cơ bản về môn Ngữ Văn.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi thứ tốt nghiệp THPT Toán - THPT Phan Châu Trinh (2013-2014)

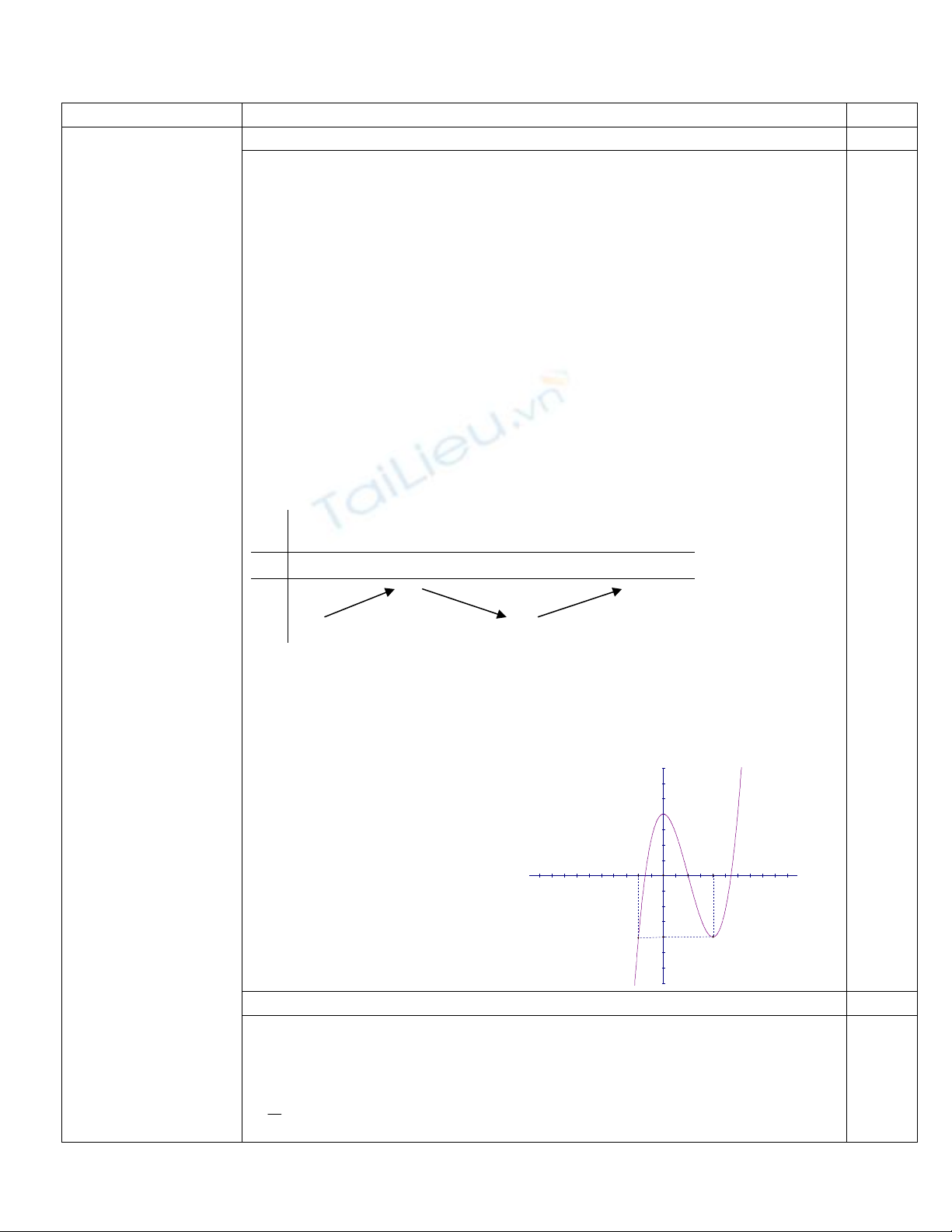
TRƯỜNG THPT PHAN CHÂU TRINH ĐỀ TOÁN THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2013- 2014 THỜI GIAN 150 PHÚT ( không kể thời gian giao đề) I.Phần chung cho tất cả thí sinh ( 7 điểm ) Câu I ( 3,0 điểm ) Cho hàm số y = x3 -3x2 +2 có đồ thị là ( C) 1.Khảo sát sự biến thiên và vẽ đồ thị (C) 2.Tìm tất cả các giá trị của tham số m để phương trình x3 -3x2 +2 = 3m có 3 nghiệm phân biệt trong đó có hai nghiệm lớn hơn 1 Câu II ( 3,0 điểm ) 2 1.Giải bất phương trình : log 1 (x  2x)  1 3 1 2.Tính tích phân : I   x2 1  x dx 0 3.Cho hàm số f(x) = x3 – 3x2 – 9x +1.Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số f(x) trên  2;2 .Suy ra các giá trị của a để bất phương trình sau có nghiệm trên đoạn  2;2 : f (x)  a 2  2a  6 ,a  R Câu III ( 1,0 điểm ) Cho hình lăng trụ tam giác đều ABC.A/B/C/ cạnh AB = a. Đường chéo BC/ của mặt bên BB/C/C tạo với mặt bên AA/B/B một góc 300. Tính thể tích khối trụ ngoại tiếp khối lăng trụ ABC.A/B/C/ II.PHẦN TỰ CHỌN ( 3 điểm ) Thí sinh chỉ được chọn một trong hai đề của phần đề A hoặc phần đề B A. Theo chương trình chuẩn Câu IV.a ( 2,0 điểm ) Trong không gian Oxyz cho điểm A(3;-2;-2) và mặt phẳng (Q): x + 2y + 3z – 7 = 0. 1.Viết phương trình mặt cầu (S) tâm A và tiếp xúc với mặt phẳng ( Q) 2.Tính tọa độ tiếp điểm H của ( S) và mặt phẳng ( Q) Câu V.a ( 1,0 điểm ) Tìm các giá trị thực của x và y để các số phức z1  9 y 2  4  10 xi 5 và z2  8 y 2  20i11 là liên hợp của nhau. B.Theo chương trình nâng cao Câu IV.b (2 điểm) Trong không gian với hệ toạ độ Oxyz , cho mặt phẳng   và đường thẳng d lần lượt có phương trình: x  2  t   : x  2 y  3z  7  0 ; d :  y  2t  z  7  t  1.Xét vị trí tương đối giữa đường thẳng d và mặt phẳng   .Tính khoảng cách giữa d và   2.Viết phương trình mặt cầu tâm I(-3;2;-2),cắt đường thẳng d tại hai điểm A,B sao cho AB=8. Câu V.b(1 điểm) Tính diện tích hình phẳng giới hạn bởi parabol (P): y  x 2  2 x  2 , tiếp tuyến của (P) tại M(3;5) và trục Oy 1
ĐÁP ÁN Câu Nội dung Điểm Câu I (3 điểm) 1.(2,0 điểm) a)TX Đ DR 0,25 b)sự biến thiên *Chiều biến thiên: y /  3 x 2  6 x ;y/=0  x = 0 hoặc x = 2 0,25 y/ >0 trên khoảng  ;0  và  2;  0,25 y/
Câu II (3 điểm) 1.( 1điểm) Điều kiện x < 0 hay x > 2 0.25 Bất phương trình thành x2 – 2x – 3 < 0 0.25  -1 < x < 3 0.25 Giao với điều kiện nghiệm bất phương trình là -1 < x < 0 hay 2 < x < 3 0.25 2.( 1điểm) Đặt t = 1  x  t 2  1  x  dx  2tdt 0.25 Đổi cận : x = 0  t  1 ; x = 1  t  0 0.25 1 1  t 7 2t 5 t 3  0.25 Ta được I = 2  t  2t  t dt = 2   6 4 2   0 7 5 3 0 16 = 0.25 105 1.( 1điểm) f/(x) = 3(x2 -2x -3 ) = 0  x  1; x  3 ( loại ) 0.25 f(-2) = -1; f(-1) = 6 ; f(2) =-21 0.25 max f (x)  6; min f (x)  21 0.25  2;2  2;2 Theo đề 6 = max f (x) > a2 +2a + 6  a2 + 2a < 0  2  a  0 0.25  2;2  Câu III (1.điểm) * Xác định được góc C/BI bằng 300 0.25 * Tính được độ dài BB/ = a 2 0.25 0.25 a 3 * Tính được bán kính R = 3  2a 3 0.25 * Tính được thể tích khối trụ bằng V = 3 A/ C/ I B/ A C B Câu IV.a 1.( 1 điểm ) (2,0 điểm) *Bán kính mặt cầu : R=d  A;(Q)  0,25 3
3 467 14 0,25 * d  A;(Q)    14 14 0,25  14 0,25 2 2 2 *Phương trình mặt cầu là  x  3   y  2    z  2   14 2.(1 điểm)  *Vectơ pháp tuyến của mặt phẳng (Q) là n  (1;2;3) 0,25 *đường thẳng d đi qua tâm A của mặt cầu và vuông góc với mặt phẳng  (Q) nhận n  (1;2;3) làm vectơ chỉ phương có phương trình x  3  t  0,25 d :  y  2  2t  z  2  3t  *Xét phương trình giao điểm của d và (Q) ứng với tham số t : 3 + t + 2(-2 + 2t) + 3(- 2 + 3t ) – 7 = 0 0,25  14t  14  t  1 * Tọa độ tiếp điểm của mặt cầu (S) và mặt phẳng (Q) là H(4;0;1) 0,25 Câu V.a 2 * Thu gọn z1  9 y  4  10 xi; z 2  8 y  20i 2 0,25 ( 1,0 điểm ) 10x  20 2 2 * Để z1  z2 ta có hệ 9 y  4  8 y 0,25  y   2 0,25 x =-2 * kết luận x = -2 và y = 2 hay x = -2 và y = -2 0,25 Câu IVb.(2điểm) 1(1.điểm) mặt phẳng   có vectơ pháp tuyến n  1;2;3 0,25 đường thẳng d có vectơ chỉ phương u   1;2;1 ; M(2;0;7) (d ) 0,25 n.u  0 và M  ( ) nên d //   0,25 2  21  7 16 8 14 d (d ;  )  d M ;      0,25 1 4  9 14 7 2.(1 điểm) Gọi r là bán kính mặt cầu tâm I, H là trung điểm của AB. 0,25 Ta có HA=4;     Do IM  (5; 2;9),[u , IM ]  (16;4; 8)    0,25 [u , IM ] IH= d(I;d)=   2 14 |u| 0,25 Suy ra bán kính của mặt cầu: R= HA2  IH 2  72 Phương trình mặt cầu có tâm I và bán kính r là: 2 2 2  x  3   y  2    z  2   72 0,25 4
Câu V.b(1,0điểm ) Phương trình tiếp tuyến d của (P) tại M: y  4 x  7 0,25 Phương trình hoành độ giao điểm của (P) và d: x 2  2x  2  4x  7  x  3 0,25 3 S  x 2  6 x  9 dx 0,25 0 vậy 3  x3  0,25    3x2  9 x   9  3 0 5