zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Luận Văn - Báo Cáo

» Khoa học tự nhiên

DÒNG ĐIỆN TRONG KIM LOẠI - ỨNG DỤNG VÀ MỘT SỐ BÀI TẬP ÁP DỤNG

Chia sẻ: Nhung Nhung | Ngày: | Loại File: PDF | Số trang:38

Báo xấu

667
lượt xem 45
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

A- MỞ ĐẦU 1. Lý do chọn đề tài 2. Mục đích nghiên cứu 3. Phạm vi nghiên cứu 4. Tình hình nghiên cứu 5. Phương pháp nghiên cứu B- NỘI DUNG Chương I: Cơ sở lý thuyết 1.1. Khái niệm 1.2. Bản chất của các hạt mang điện trong kim loại 1.3. Cơ sở lý thuyết cổ điển về kim loại 1.3.1. Khái niệm cơ bản 1.3.2. Định luật Ohm 1.3.3. Định luật Joule - Lenz 1.3.4. Định luật Wiedeman - Franz 1.3.5. Những nhược điểm của lý thuyết điện tử cổ điển về sự dẫn điện của...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: DÒNG ĐIỆN TRONG KIM LOẠI - ỨNG DỤNG VÀ MỘT SỐ BÀI TẬP ÁP DỤNG

Bài tập tiểu luận Huỳnh Trọng Dương DÒNG ĐIỆN TRONG KIM LOẠI - ỨNG DỤNG VÀ MỘT SỐ BÀI TẬP ÁP DỤNG MỤC LỤC: A- MỞ ĐẦU 1. Lý do chọn đề tài 2. Mục đích nghiên cứu 3. Phạm vi nghiên cứu 4. Tình hình nghiên cứu 5. Phương pháp nghiên cứu B- NỘI DUNG Chương I: Cơ sở lý thuyết 1.1. Khái niệm 1.2. Bản chất của các hạt mang điện trong kim loại 1.3. Cơ sở lý thuyết cổ điển về kim loại 1.3.1. Khái niệm cơ bản 1.3.2. Định luật Ohm 1.3.3. Định luật Joule - Lenz 1.3.4. Định luật Wiedeman - Franz 1.3.5. Những nhược điểm của lý thuyết điện tử cổ điển về sự dẫn điện của kim loại 1.4. Sơ lược về lý thuyết hiện đại về tính dẫn điện của vật rắn 1.5. Giải thích tính chất điện của kim loại 1.5.1. Bằng thuyết electron 1.5.2. Bằng lý thuyết dải năng lượng của thuyết lượng tử 1.6. Hiện tượng ở chổ tiếp xúc giữa các kim loại Chương II: Ứng dụng của kim loại 2.1. Ứng dụng của hiện tượng nhiệt điện 2.1.1. Nhiệt kế nhiệt điện 2.1.2. Pin nhiệt điện 2.1.3. Máy lạnh sử dụng hiệu ứng nhiệt điện 2.2. Ứng dụng của siêu dẫn để tạo tàu chạy trên đệm từ Chương III: Một số bài tập áp dụng C- KẾT LUẬN TÀI LIỆU THAM KHẢO 1 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương A- MỞ ĐẦU 1. Lý do chọn đề tài Như chúng ta đã biết, đa số các ứng dụng của điện đều liên quan đến dòng điện. Trong mỗi môi trường khác nhau chúng ta lại có những dòng điện với những ứng dụng khác nhau. Trong đó, dòng điện chạy trong dây dẫn kim loại là một trong những dòng điện có ứng dụng rất quan trọng trong đời sống con người, nó cung cấp năng lượng điện cho các dụng cụ điện trong gia đình như đèn chiếu sáng, bàn là, tủ lạnh… Nói đến kim loại có lẽ không ai là không biết và mọi người cũng biết rõ kim loại dẫn điện rất tốt. Vì tính dẫn điện rất tốt này với việc nhiều kim loại có giá rẽ và nhiều nên chưa có một vật liệu nào hoàn toàn thay thế được vai trò của nó. Tuy nhiên, việc hiểu rõ bản chất, cấu trúc của kim loại cũng như nguyên lý hoạt động của dòng điện trong kim loại – dòng chuyển động của các điện tích thì không phải ai cũng biết và đó cũng là bí ẩn của nhiều người. Đa số mọi người biết về kim loại cũng như dòng điện trong kim loại với những ứng dụng khác nhau như pin nhiệt điện, máy lạnh sử dụng hiệu ứng nhiệt điện hay tàu chạy trên đệm từ,…nhưng lại không biết làm cách nào để có thể có những ứng dụng đó. Rất nhiều thắc mắc được đặt ra trong tôi như hoạt động của dòng điện trong kim loại dựa vào đâu? Tính dẫn điện của nó dựa vào cái gì? Hay ứng dụng đó được dựa vào tính chất nào? … Từ đó tôi quyết định đi nghiên cứu về đề tài “ Dòng điện trong kim loại - ứng dụng và một số bài tập áp dụng” để có thể làm sáng tỏ những thắc mắc đó. Bên cạnh việc giải thích bản chất, tính chất dẫn điện của kim loại, nói đến ứng dụng tôi còn tiến hành tìm kiếm, sưu tầm bài tập áp dụng cho phần này để tôi cũng như các bạn hiểu rõ hơn. Có thể nói đề tài này không phải là một đề tài mới mẽ, nhưng ý nghĩa của nó thì không bao giờ cũ, không bao giờ mất đi và luôn giữ một ý nghĩa hết sức quan trọng. 2. Mục đích nghiên cứu Với lý do trên, tôi đã đi đến quyết định nghiên cứu đề tài này nhằm giúp tôi cũng như mọi người – những người quan tâm đến vấn đề này hiểu rõ hơn về dòng điện trong kim loại cả về bản chất, cấu trúc, tính chất dẫn điện của kim loại và ứng dụng cũng như bài tập áp dụng. Và quan trọng hơn là tôi muốn giúp các bạn học sinh trung học phổ thông, đặc biệt là các bạn lớp 11 hiểu rõ hơn về dòng điện trong kim loại, biết cách vận dụng lý thuyết để giải các bài tập liên quan. Từ đó có hứng thú học tập môn vật lý hơn, ham muốn học hỏi, sáng tạo, tìm tòi nghiên cứu sâu hơn về các hiện tượng vật lý, góp phần vào việc phát triển đất nước. 3. Phạm vi nghiên cứu Tôi đi sâu vào việc giải thích bản chất của dòng điện trong kin loại, tìm hiểu những lý thuyết liên quan đến dòng điện trong kim loại, và một số bài tập áp dụng. Nội dung bài này không rộng, tôi chỉ nêu lên về lý thuyết mà không đi vào thực nghiệm nhưng lại chú trọng đến phần bài tập dành cho các bạn đang học tập, các bạn thích nghiên cứu vấn đề này, đặc biệt là các bạn lớp 11. 4. Tình hình nghiên cứu 2 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương Vì đây không phải là đề tài mới nên việc tìm tài liệu cho đề tài này không khó nhưng cũng vì được nhiều người nghiên cứu nên việc chọn lọc những kiến thức phù hợp và có ý nghĩa cũng có phần khó khăn. 5. Phương pháp nghiên cứu  Tìm kiếm, thống kê, phân tích  Quy nạp diễn dịch  Lôgic tổng hợp  Nhận xét, đánh giá 3 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương B- NỘI DUNG Chương I: Cơ sở lí thuyết 1.1. Khái niệm Dòng điện trong kim loại là dòng các electron tự do chuyển dời có hướng dưới tác dụng của điện trường ngoài (ngược chiều điện trường) Đối với riêng một nguyên tử kim loại: Các electron ở lớp vỏ ngoài cùng dễ mất liên kết với hạt nhân, trở thành các electron tự do. Lúc đó, nguyên tử trở thành ion dương. Đối với toàn khối kim loại: – Các ion dương được sắp xếp một cách đều đặn theo một trật tự nhất định trong không gian, tạo thành mạng tinh thể. – Mỗi nút mạng là một ion dương dao động nhiệt quanh vị trí cân bằng của mình. – Các electron bị mất liên kết với hạt nhân của nguyên tử kim loại, thì chuyển động tự do trong khoảng không gian giữa các ion dương (nút mạng). Các electron này được gọi là electron tự do; chúng có vai trò là hạt tải điện, nên gọi là electron dẫn. – Giữa ion dương và electron tự do có lực hút tĩnh điện. – Tổng đại số điện tích âm của các electron tự do bằng tổng đại số điện tích dương của các ion dương, nên toàn khối kim loại trung hòa về điện. 1.2. Bản chất của các hạt mang điện trong kim loại. Người ta đã tiến hành nhiều thí nghiệm để khám phá bản chất các hạt mang điện trong kim loại. Trước hết ta hãy kể đến thí nghiệm do nhà vật lý người Đức Carl Riecke (1845- 915) tiến hành vào năm 1912. Ông đã dùng ba vật dẫn hình trụ, hai bằng đồng và một bằng nhôm với các đầu được đánh bóng kỹ càng. Sau khi cân các thanh hình trụ được đặt kế tiếp nhau theo thứ tự đồng - nhôm - đồng và cho dòng điện chạy qua tổ hợp ba hình trụ dẫn đố trong thời gian một năm. Như vậy, trong thời gian này đã có 3,5.10 6 C chạy qua. Sau đó người ta đem các thanh hình trụ này ra cân lại thì thấy trọng lượng của chúng không hề thay đổi. Soi bằng kính hiển vi các đầu của các hình trụ ta cũng không thấy có sự xâm nhập vật chất từ các thanh dẫn khác. Kết quả thực nghiệm này chứng tỏ rằng các hạt mang điện không phải là nguyên tử mà là các hạt có trong tất cả các kim loại. Các điện tử mà J.J Thomson phát hiện ra trong năm 1897 có thể là các hạt mang điện đó. Để khẳng định được các hạt mang điện trong kim loại là các hạt điện tử ta cần phải xác định được dấu cũng như độ lớn điện tích của các hạt mang điện trong kim loại. Ý tưởng như sau: Nếu kim loại chứa các hạt mang điện có thể chuyển động thì nếu khi vật dẫn kim loại bị giảm tốc thì các hạt đó thao quán tính vẫn tiếp tục chuyển động trong một khoảng thời gian nào đó và làm xuất hiện một dòng điện đảy đồng thời có mọt số hạt sẽ thoát ra khỏi kim loại. 4 SVTH: Phạm Thị Tiên
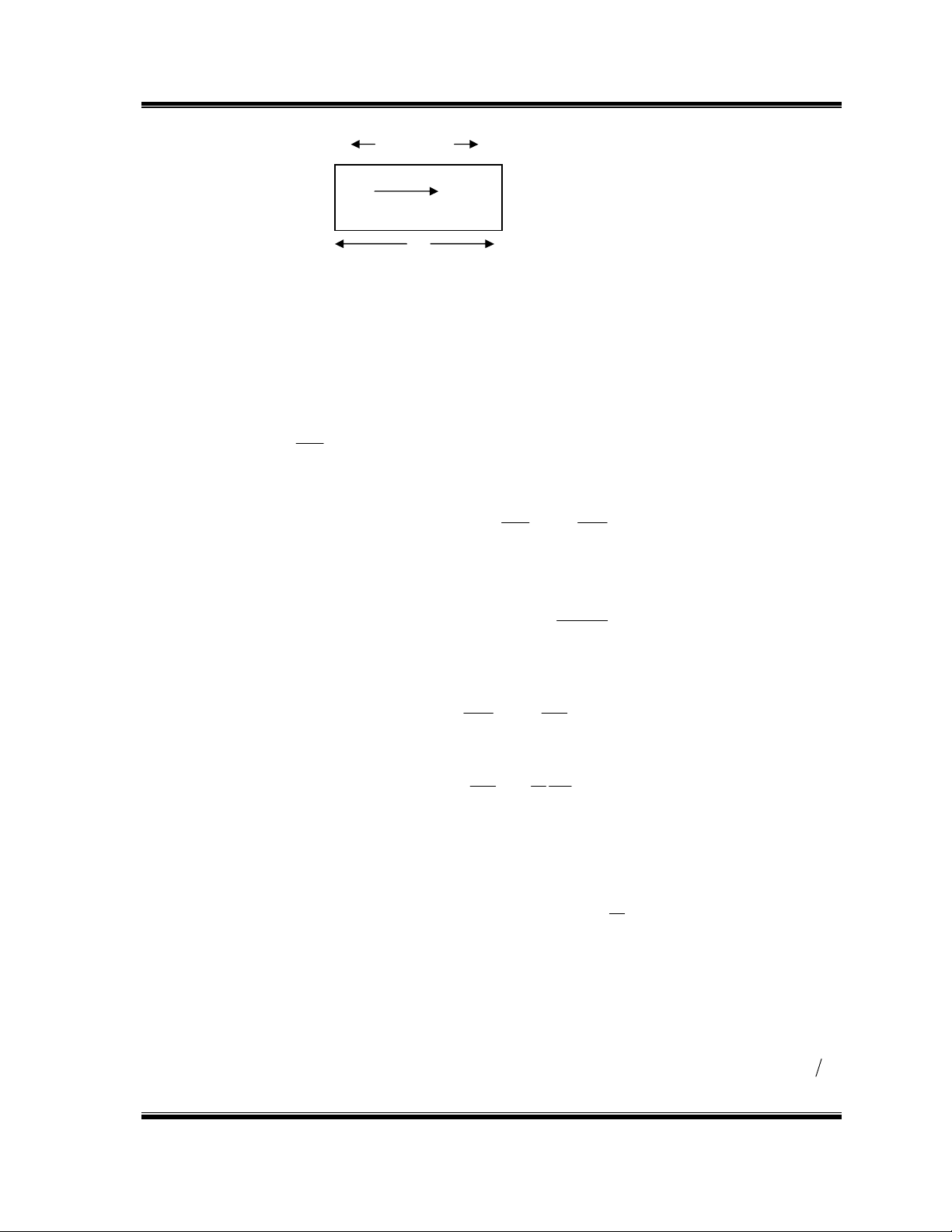
Bài tập tiểu luận Huỳnh Trọng Dương   a v0  e' a 0 i Hình 1: Hạt mang điện trong kim loại  Giả sử lúc đầu dây dẫn được chuyển động với vận tốc v0 .  Ta tiến hành giảm tốc với giá trị của gia tốc bằng a . Do quán tính các hạt mang  điện sẽ tiếp tục chuyển động với gia tốc - a so với vật dẫn. Mỗi gia tốc như vậy sẽ chuyển cho các hạt mang điện đứng yên trong vật dẫn và tạo trong đó một điện  ma trường bằng    1 . Điều này có nghĩa là tạo nên hai đầu vật dẫn một hiệu điện e thế bằng:  2  2 ma  mal V1  V2    dl    ' dl   ' 1 1 e e trong đó: m, e ' là khối lượng và điện tích của hạt tải điện, l là độ dài của dây dẫn. V1  V2 Trong trường hợp này sẽ có dòng điện I = , với R là điện trở của dây R dẫn, chạy dọc theo hướng chuyển động của dây dẫn. Như vậy sẽ có dòng điện tích dq chạy qua các tiết diện trong thời gian dt với: mal ml dq  dt   ' dt   ' dv eR eR Số điện tích chạy qua các tiết diện trong suốt thời gian giảm tốc sẽ là: t 0 ml m lv q   dq   ' dv  ' 0 (1) 0 v0 e R e R Điện tích q dương nếu như nó được chuyển theo hướng chuyển động của dây dẫn. Như vậy nếu đo được l, v 0 , r cũng như lượng điện tích q chuyển qua dây dẫn e' trong thời gian giảm tốc ta có thể xác định được tỷ số của hạt mang điện trong m dây dẫn. Hướng của xung dòng sẽ cho biết dấu của điện tích của hạt mang điện. Theo hướng này hai nhà bác học người Nga là Leonid Mandenshtam(1879 - 1944) và Nikolai Papaleksi (1880 - 1947) đã tiến hành thí nghiệm vào năm 1913. Các ông đã thu được các kết quả có tính chất định tính. Năm 1916 hai nhà vật lý người Mỹ là R. Tolman và T. Stewart đã thu được các kết quả định lượng. Một cuộn dây dài 500m được quay với vận tốc dài bằng 300 m s . Dây được hãm lại đồng thời người ta dùng một điện kế xung kích để đo lượng điện 5 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương e' e tích chạy qua dây. Kết quả tỉ lệ đo được theo thí nghiệm này gần với giá trị của m m điện tử. Điều này chứng tỏ rằng các hạt mang điện trong kim loại chính là các điện tử. Trong kim loại với một số hiệu điện thế rất bé người ta cũng có thể tạo nên dòng điện, điều đó cho ta cơ sở để có thể khẳng định rằng các hạt mang điện – điện tử có thể chuyển động mà không bị cản trở. Sự tồn tại của điện tử trong kim loại được giải thích như sau:Khi mạng tinh thể được hình thành, các điện tử có liên kết yếu nhất (điện tử hóa trị) tách ra khỏi nguyên tử và trở thành các điện tử chung của toàn mẫu kim loại. Nếu cứ một điện tử tách ra khỏi một nguyên tử thì nồng độ các điện tử tự do (số điện tử n trong một đơn vị thể tích) sẽ bằng số nguyên tử của một đơn vị thể tích. Mà số nguyên tử trong một  đơn vị thể tích bằng N A . Trong đó  là khối lượng riêng của kim loại, M là khối M  lượng riêng của một mol kim loại đó, NA là số Avogadro, của Kali khoảng 2.104 M 3 28 29 3 mol m . Vì vậy đối với kim loại: n  10  10 / m 1.3. Cơ sở lý thuyết cổ điển về kim loại. 1.3.1. Khái niệm cơ bản Dựa trên sự tồn tại của điện tử tự do (tập thể), nhà vật lý học người Đức Paule Drude (1836 – 1906) đã đưa ra lý thuyết cổ điển về kim loại và tiếp sau được H.Lorentz hoàn chỉnh. Drude cho rằng các điện tử dẫn trong kim loại giống như các phân tử trong khí lý tưởng. Trong khoảng giữa hai va chạm chúng chuyển động hoàn toàn tự do trên một quảng đường l nào đó. Nhưng khác với các phân tử khí trong khí lý tưởng mà trong đó các phân tử va chạm với các phân tử khác, trong kim loại các điện tử tự do chủ yếu không va chạm với các điện tử khác mà và chạm với các ion tạo nên mạng tinh thể của kim loại. Các va chạm này dẫn đến việc thiết lập cân bằng nhiệt giữa các khí điện tử và mạng tinh thể. Khi cho một điện trường tác dụng lên kim loại thì các chuyển động có hướng   của các điện tử u sẽ chồng chất với vận tốc chuyển động nhiệt v . Ta có thể xác định  vận tốc chuyển động có hướng u của các điện tử theo công thức:   j  ne u Trong đồng, mật độ dòng cực đại khoảng 107 A/m2 và với giá trị n  10 29 / m 3 ta có: _ j 10 7 u  29 19  10 3 m / s ne 10 .(1,6.10 ) Như vậy ngay cả khi có mật độ dòng cực đại, vận tốc chuyển có hướng của các _ điện tử u cũng chỉ đạt khoảng 1/108 vận tốc chuyển động nhiệt trung bình của nó. Do 6 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương đó trong khi tính toán ta thường lấy giá trị tuyệt đối của vecto vận tốc tổng    v  u bằng giá trị tuyệt đối của vận tốc chuyển động nhiệt v . Muốn vậy, ta hãy tìm sự thay đổi động năng trung bình của điện tử khi có trường điện, ta có: 2   2   2  2  2  v  u    v  2 v u u   v  2v u  u         Vì u và v độc lập với nhau nên có thể tính lại số hạng thứ hai trong biểu thức trên:  uv 0  Vì v =0 do đó: 2 2 2      v u   v  u   Như vậy động năng trung bình của điện tử tăng lên một lượng: mu 2 W k  2 1.3.2. Định luật Ohm. Drude cho rằng khi điện tử va chạm với các ion của mạng tinh thể, sự thay đổi động năng mà điện tử thu được khi có điện trường truyền hết cho ion, cho nên sau  va chạm đó vận tốc u không còn nữa. Ta còn giả thiết điện trường đồng nhất cho nên điện tử luôn nhận được một gia tốc không đổi bằng Ee/m và khi đạt đến va chạm mới, có thể xem vận tốc cực đại của nó bằng: eE u max   m trong đó  là khoảng thời giant rung bình giữa hai va chạm của điện tử với ion của mạng tinh thể. Drude không khảo sát sự phân bố vận tốc của các điện tử và cho rằng tát cả các điện tử ddeuf có cùng vận tốc v, vì vậy gần đúng ta có: l  v eEl Vì vậy: u max  mv Vận tốc u thay đổi tuyến tính trên quảng đường l, do đó giá trị trung bình của nó trên quảng đường l này bẳng giá trị cực đại: 1 eEl u u max  2 2mv Từ đó độ lớn mật độ dòng j có dạng: ne 2 l j E 2mv So sánh biểu thức này với định luật Ohm dưới dạng vi phân ta có thể rút ra: 7 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương ne 2 l  2mv Nếu điện tử không va chạm với các ion trong mạng tinh thể thì quảng đuờng tự do của nó, và do đó độ dẫn điện của kim loại sẽ vô cùng lớn. Như vậy theo lý thuyết cổ điển , điện trở của kim loại là do va chạm của các điện tử tự do với các ion trong mạng tinh thể gây nên. 1.3.3. Định luật Joule –Lenz Tại cuối đoạn đường chuyển động tự do l, khi có điện trường ngoài mỗi điện tử mu 2 eEl nhận thêm một động năng Wk  . Nếu tính đến u max  ta có: 2 mv 2 mu max e 2l 2 2 Wk   E 2 2mv 2 Như Drude đã giả định , khi va chạm với các ion, điện tử truyền hết năng lượng vừa nhận them được cho ion. Lượng năng lượng làm tăng nội năng của mạng tinh thể kim loại và được thể hiện qua việc kim loại bị nóng lên. Mỗi một điện tử trong một đơn vị thời gian (1s) trung bình chịu 1/ =v/l va chạm, và mỗi lần va chạm lại truyền hết năng lượng vừa thu được cho mạng tinh thể, vì vậy mà năng lượng nhiệt thoát ra trong một đơn vị thể tích bằng: 1 ne 2 l 2 Qu  n Wk    2mv trong đó n là số điện tử dẫn trong một đơn vị thể tích. Đại lượng Qn chính là công suất nhiệt của dòng điện. Hệ số của E2 trong công thức trên theo Ohm chính là độ dẫn điện  của kim loại. Lại theo định luật Ohm dưới dạng vi phân j =  E ta có:  22 Qu  E 2   j 2  Đây chính là biểu thức của định luật Joule – Lenz dưới dạng vi phân. 1.3.4. Định luật Wiedeman – Franz Thực nghiệm đã chứng tỏ rằng, kim loại ngoài tính dẫn điện tốt còn có độ dẫn nhiệt cao. Hai nhà vật lý học người Đức là G. Wiedeman và R. Franz đã thiết lập được định luật thực nghiệm về tỷ số giữa độ dẫn nhiệt  và độ dẫn điện  của kim loại. Theo định luật này, tỷ số giữa  và  đối với tất cả kim loại gần như nhau, thay đổi tỷ số với nhiệt độ tuyệt đối. Ví dụ tỷ số này tại nhiệt độ trong phòng đối với nhôm là 5,8.10-6, đồng là 6,4.10 -6, chì là 7,0.10-6 J.  /(s.K ) Các tinh thể không kim loại cũng có khả năng dẫn nhiệt. Tuy nhiên độ dẫn nhiệt của kim loại trội hơn nhiều độ dẫn nhiệt của các chất điện môi. Điều đó là vì các điện tử tự do chứ không phải là mạng tinh thể, chính là các yếu tố truyền nhiệt. Từ đó: 1  nkvl 2 8 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương ne 2 l 3 1 Chia  cho biểu thức của độ dẫn điện   và trong đó thay kT  mv 2 ta 2mv 2 2 có biểu thức: 2  kmv 2 k  2  3  T  e e Biểu thức này thể hiện định luật Wiedeman – Franz. Thay giá trị bằng số, ta có công thức tính:   2,23.10 8 T  Khi T=300K, tỷ số   bằng 6,7.10-6 J.  /(s.K ) . Giá trị lý thuyết này phù hợp với các số liệu thực nghiệm. Tuy nhiên điều phù hợp này thật ra không đúng vì sau này H.Lorentz đã tiến hành tính toán với mức độ chính xác cao hơn bằng cách chú ý đến sự phân bố của 2  k điện tử theo vận tốc và ông đã thu được công thức  2  T . Kết quả này không    e phù hợp với các số liệu thực tế. 1.3.5. Những nhược điểm của lý thuyết điện tử cổ điển về sự dẫn điện của kim loại. Lý thuyết cổ điển về kim loại đã giải thích được các định luật Ohm, định luật Joule –Lenz, Wiedeman – Franz nhưng lại có những nhược điểm sau:  Không thể giải thích được quy luật quan sát được bằng thực nghiệm về sự phụ thuộc tuyến tính giữa điện trở suất  và nhiệt độ T. Như vậy lý thuyết mâu thuẫn với thực nghiệm.  Theo lý thuyết cổ điển nhiệt dung phân tử đẳng tích của kim loại phải lớn hơn 1,5 lần nhiệt dung của chất điện môi. Tuy nhiên thực nghiệm chứng tỏ rằng nhiệt dung phân tử của kim loại không khác nhiều so với nhiệt dung phân tử của các tinh thể phi kim loại. Chỉ có lý thuyết lượng tử về kim loại mới khắc phục được các nhược điểm này. 1.4. Sơ lược về lý thuyết hiện đại về tính dẫn điện của vật rắn. Lý thuyết lượng tử là cở sở để nghiên cứu đầy đủ về tính dẫn điện của vật rắn. Theo cơ học lượng tử, hệ hạt chỉ có thể tồn tại ở trạng thái năng lượng xác định. Hệ hạt chuyển từ trạng thái này sang trạng thái khác một cách nhảy vọt, tương ứng với một biến đổi năng lượng xác định. Ví dụ xét một điện tử trong trường tĩnh điện của một ion dương. Theo cơ học lượng tử, năng lượng toàn phần của điện tử trong miền giá trị âm chỉ có thể có một trong những giá trị sau:  W=  n2 9 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương trong đó B là một hằng số và n là số nguyên dương (n = 1,2,...). Năng lượng tương  ứng với W =  được điểu diễn bằng các đường nằm ngang trên hình 2. n2 Theo thuyết cổ điển 1 q.q 0 C W=   4 r r Hình 2: Các mức năng lượng của điện tử trong trường Coulomb Phân bố lượng tử của điện tử theo mức năng lượng khác hẳn với phân bố cổ điển. Đó là do theo cơ học lượng tử, các điện tử tuân theo nguyên lý loại trừ Pauli. Nguyên lý này như sau: Trong cùng một mức năng lượng (với điều kiện không suy biến) có tối đa hai điện tử spin ngược nhau. Tại nhiệt độ không tuyệt đối, theo quan điểm cổ điển động năng của tất cả các điện tử phải bằng không. Nhưng theo nguyên lý Pauli, nếu số điện tử tự do trong kim loại bằng n thì khi T = 0K chúng chiếm n/2 mức năng lượng thấp nhất. Trong trường hợp này, định luật phân bố điện tử theo các mức năng lượng là đường gãy khúc 2 trên hình 3. n n 3 1 2  w 2kT Hình 3: Phân bố điện tử theo mức năng lượng 1- Phân bố Maxwell- Bolzmann 2- Phân bố Fermi- Dirac 3- Phân bố Bose - Einstein 10 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương Trên hình 3 WFi là năng lượng ứng với mức trên cùng còn chứa đầy điện tử tại nhiệt độ không đổi. Như vậy tại T = 0K, tất cả các mức năng lượng Wi < WFi (được gọi là thế hóa học  ) đều chứa đầy điện tử, mỗi mức có 2 điện tử, còn những mức năng lượng Wi > WFi đều trống. Theo lý thuyết lượng tử, sự phân bố của các điện tử theo các mức năng lượng tuân theo hàm phân bố Fermi - Dirac: 1 1 fF  W   Wd WF kT kT e 1 1 e Trong đó W,  , Wd ,WF là năng lượng được biểu diển trên hình 4.  được gọi là U  TS  pV thế hó học có giá trị bằng:   (k là hằng số Boltzman, T là nhiệt độ N tuyệt đối, U nội năng, S entropy, N số Avogadrro). W r W WFi Wd WF Hình 4: Các mức năng lượng. Tổng quát, hàm phân bố trong thống kê cổ điển và thống kê lượng tử biểu diễn số các hạt trung bình trong mỗi trạng thái năng lượng dưới cùng một công thức thống nhất: 1 fF  W  kT e  Khi  = 0,   0 ta có phân bố Maxwell- Bolzmann   1 : phân bố Bose - Einstein   1 : phân bố Fermi- Dirac Trên hình 3 là các đường cong f F với các nhiệt độ khác nhau. Khi T = 0, đường W  cong phân bố f F là đường cong 2. Thật vậy, khi T = 0, nếu W <  thì e kT  thì e >>1 nên f F =0. Khi T > 0 đường biểu diễn hàm f F kT là đường cong số 3. Đường cong 1 biểu diễn phân bố Maxwell- Bolzmann. Tại nhiệt độ cao đường cong phân bố Fermi- Dirac tiến gần đến đường cong phân bố Maxwell- Bolzmann. 11 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương Các kết luận ở trên đúng cho một hệ nguyên tử bất kỳ. Giản đồ năng lượng của các điện tử trên những quỹ đạo khác nhau của một nguyên tử được vẽ trên hình 5. Điều đặc biệt quan trọng là hình ảnh định tính về sự phân bố các mức năng lượng của điện tử trong vật rắn cũng tương tự như trong nguyên tử cô lập. Theo nguyên lý Pauli thì trạng thái các điện tử trong một hệ bất kỳ phải khác nhau. Hình 5: Phân bố điện tử theo các mức năng lượng trong một nguyên tử 1 1 Trong biểu thức f F  W   Wd WF khi biểu diễn thế năng của điện tử kT kT e 1 1 e trong kim loại, ta chọn thế năng của điện tử ở điểm xa vô cùng bằng không, do đó các mức năng lượng của điện tử trong kim loại là âm: W,  < 0. Trong một số trường hợp khác, để thuận tiện cho việc biểu diễn ta chọn mức thế năng ở đáy hố thế năng trong kim loại bằng không, khi đó các mức năng lượng Fermi W > 0 và năng lượng toàn phần của điện tử trong hố thế năng của kim loại là Wd > 0, Wd cũng chính là động năng của điện tử trong hố thế năng này. Theo nguyên lý Pauli thì trạng thái của điện tử trong một hệ bất kỳ phải khác nhau. Những trạng thái khác nhau của điện tử tương ứng với những năng lượng khác nhau, mặt dù sự khác nhau đó có thể rất nhỏ. Lý thuyết lượng tử chứng tỏ rằng nếu nguyên tử phân bố trong tinh thể một cách đều đặn thì những điện tử này hoàn toàn không bị ràng buộc với một nguyên tử xác định nào cả và có thể chuyển động trong mạng tinh thể như các điện tử tự do. Phép tính cơ học lượng tử phân tích chuyển động của điện tử trong tinh thể đã chứng tỏ rằng: nếu số nguyên tử tạo thành tinh thể là N thì một mức của điện tử hóa trị trong nguyên tử cô lập tương ứng với N mức riêng biệt phân bố rất gần nhau trong tinh thể. Trong tinh thể thực, số nguyên tử N rất lớn, nên N các mức riêng biệt rất gần nhau này tạo thành một giải hoặc một vùng những trạng thái được phép. Bề rộng vùng  thực tế không phụ thuộc vào N. Khi N lớn, điện tử tự do có thể chuyển động dễ dàng từ mức này sang mức khác nằm trong giới hạn của một vùng được cho phép (hình 6). 12 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương Vùng cho Mức năng lượng trong nguyên phép 1 tử cô lập Vùng cấm d Sự thay đổi mức năng lượng theo khoảng cách tương đối T Vùng cho 2 phép r0 Hình 6: Phân bố năng lượng trong tinh thể Trong nguyên tử cô lập, điện tử hóa trị có một vài mức được phép, cho nên trong tinh thể cũng có một vài vùng được phép của điện tử, vùng nọ cách vùng kia một khoảng có chiều rộng d cỡ bằng  . Vùng có chiều rộng d giữa hai vùng được phép là vùng cấm. 1.5. Giải thích tính chất điện của kim loại. 1.5.1. Bằng thuyết electron.  Tính dẫn điện tốt của kim loại Kim loại dẫn điện tốt vì mật độ electron tự do trong kim loại rất lớn. Tính dẫn điện của kim loại được giải thích như sau: Các electron tự do trong kim loại có tốt độ rất lớn (cỡ 10 5 m / s ). Chuyển động nhiệt hỗn độn tán xạ trên các chỗ mất trật tự của mạng tinh thể nên không có hướng ưu tiên. Xét số electron chuyển động theo một chiều nào đó, về trung luôn bằng số electron chuyển động theo chiều ngược lại. Điện lượng tổng cộng bởi các electron đi qua một mặt bất kỳ theo một chiều nào đó là bằng không. Vậy chuyển động hỗn loạn của các electron tự do không tạo ra dòng điện trong vật dẫn kim loại (hình 7a).    0  a b Hình 7: Chuyển động nhiệt và chuyển động cuốn của electron trong kim loại 13 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương Khi đặt một hiệu điện thế bên ngoài vào hai đầu của vật dẫn kim loại, do chịu tác dụng của lực điện trường, các electron tự do nhận thêm một thành phần vận tốc chuyển động có hướng ngược chiều điện trường ngoài (hình 7b):   F  e.   trong đó F là lực do điện trường ngoài tác dụng lên một electron. Khi đó số electron chuyển động ngược với chiều điện trường ngoài sẽ lớn hơn số electron chuyển động cùng chiều với điện trường ngoài, nghĩa là xuất hiện chuyển dời có hướng của các hạt điện tích dẫn đến trong kim loại có dòng điện. Dòng điện trong kim loại là dòng dịch chuyển có hướng của các electron tự do ngược chiều điện trường ngoài tác dụng lên kim loại.  Giải thích nguyên nhân gây ra điện trường. Trong chuyển động có hướng, các electron tự do luôn tương tác với các ion nằm ở nút mạng dao động quanh vị trí cân bằng và những chỗ mất trật tự của mạng tinh thể. Giữa hai va chạm kế tiếp, các electron chuyển động có gia tốc dưới tác dụng của điện trường ngoài và nó có một năng lượng xác định do điện trường cung cấp. Sau va chạm, các electron bị tổn hao năng lượng chuyển động có hướng, nói cách khác kim loại cản trở dòng điện hay kim loại có điện trở. Nguyên nhân gây ra điện trở là do va chạm của các electron tự do và các ion dương của mạng tinh thể. Các kim loại khác nhau có cấu trúc mạng tinh thể khác nhau, do đó tác dụng cản trở chuyển động có hướng của các electron tự do của mạng tinh thể khác nhau là khác nhau, dẫn đến điện trở suất của các kim loại không giống nhau. Ngay sau khi ngắt điện trường, các electron không còn được gia tốc do điện trường nữa, quá trình chuyển động có hướng của electron nhanh chóng bị mất do va chạm. Chuyển động của các electron lại trở về quá trình chuyển động hỗn loạn do nhiệt.  Giải thích tính phụ thuộc nhiệt độ của điện trở Khi electron va chạm với nút mạng, nó truyền năng lượng nhận được từ điện trường ngoài cho nút mạng làm cho các nút mạng dao động mạnh hơn, nghĩa là kim loại nhận được năng lượng dưới dạng nhiệt. Vì vậy, khi có dòng điện chạy qua kim loại nóng lên. Khi tăng nhiệt độ của kim loại, các ion kim loại ở nút mạng dao động mạnh hơn làm tăng tiết diện tán xạ, nên electron tự do dễ va chạm với nút mạng hơn, dẫn đến điện trở suất của kim loại tăng tuyến tính với nhiệt độ của kim loại. Mô hình electron tự do đã được sử dụng để giải thích các tính chất của kim loại và đã thu được một số thành công, như đã xây dựng được biểu thức của định luật Ohm, rút ra hệ thức giữa điện trở suất và độ dẫn nhiệt. Tuy nhiên, mô hình đó đã bất lực trong việc giải thích một số hiện tuợng như vì sao electron dẫn có quãng duuờng chuyển động tự do rất lớn. Thực nghiệm cho thấy rằng, các electron dẫn có thể chuyển động không va chạm trên những khoảng cách dài bằng nhiều lần hằng số mạng (có truờng hợp đạt tới hàng xentimet). 14 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương Lý thuyết luợng tử có thể giải thích một cách đầy đủ và đúng đắn hơn các tính chất của kim loại. 1.5.2. Bằng lý thuyết dải năng lượng của thuyết luợng tử. Kim loại có số electron tự do lớn nên dẫn điện tốt. Ở độ không tuyệt đối, các electron chỉ chiếm một phần các trạng thái của dải năng lượng mà nó chiếm chỗ, trong dãi còn nhiều trạng thái năng luợng còn trống. Ta xét tinh thể chất rắn của các nguyên tử ở cột I bảng tuần hoàn các nguyên tố hoá học (nhóm kim loại kiềm). Mỗi nguyên tử có một electron hoá trị, nên ở độ không tuyệt đối các electron hoá trị chỉ chiếm một nửa các trạng thái trong dải năng luợng đó (hình 8). E =0 Hình 8: Cấu trúc dải năng luợng của kim loại kiềm Mức năng lượng cao nhất của electron chiếm chổ trong dải đuợc gọi là mức năng luợng Fermi (  F ) . Các trạng thái năng lượng trên mức Fermi còn trống, các electron trong vùng có thể di chuyển dẽ dàng. Mật độ electron tự do trong kim loại kiềm rất lớn nên đuợc gọi là “khí electron”, chúng phân bố đồng đều trong mạng luới các ion dương. Vì vậy, kim loại kiềm dẫn điện rất tốt. Các electron tự do trong kim loại ở nhịêt độ phòng có vận tốc chuyển động trung bình vT  10 5 m / s . Các electron chuyển động hỗn độn không có định huớng ưu tiên nên không sinh ra dòng điện. Các electron hóa trị có thể chuyển động tự do trong chất rắn. Nếu ta lấy gốc toạ độ tại đáy dải năng luợng đó: E = 0, ở độ không tuyệt đối, mức năng luợng cao nhất trong dải bị elẻcton chiếm gọi là năng lượng Fermi  F , vận tốc của electron tương ứng với năng luợng Fermi đuợc gọi là vận tốc Fermi v F . Đối với kim loại đồng  F  7,0eV và v F  1,6.10 6 m / s. Khi đặt kim loại vào trong điện truờng, lực điện trường gia tốc cho các electron tự do có thêm chuyển động cuốn nguợc huớng điện truờng. Chuyển động của electron lúc này bao gồm chuyển động hỡn độn và chuyển động định huớng, do đó xuất hiện chiều chuyển động ưu tiên tạo nên dòng điện. Mặc dù tốc độ trung bình của chuyển động cuốn do tác dụng của điện truờng nhỏ, nhưng khi hai đầu dây dẫn có một hiệu điện thế thì ngay lập tức dây dẫn có dòng điện. Nguyên nhân của hiện 15 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương tuợng đó là do vận tốc truyền tuơng tác của electron chính là vận tốc lan truyền của sóng điện từ 3.108 m / s. Kim loại có điện trở suất cao vì mật độ electron tự do trong kim loại lớn. Theo quan điểm lượng tử, sóng electron không va chạm khi chuyển động trong mạng tinh thể lý tưởng hoàn toàn trật tự, nên electron dẫn có quảng đưòng bị hạn chế do trong tinh thể thực luôn tồn tại các khuyết tật do sai hỏng mạng tinh thể và tạp chất. Trong tinh thể của các nguyên tử hoá trị hai (như beri, manhê, canxi, strôni, bari), mỗi nguyên tử đóng góp hai electron hoá trị vào vùng năng lượng hoá trị. Trường hợp này ta hình dung rằng dải hoá trị bị chiếm đầy, các electron hoá trị dường như không dịch chuyển được trong dải năng lượng và chất rắn như vậy không dẫn điện. Nhưng thực tế, các nguyên tố hoá trị hai đều là kim loại, có khả năng dẫn điện tốt. Lý thuyết dải năng lượng giải thích hiện tuợng này như sau: trong tinh thể các kiêm loại kiềm thổ, dải năng lượng này phủ một phần lên dải năng lượng hoá trị bị chiếm đầy (hình 9). Như vậy, elecron trong dải đầy có thể dễ dàng chuyển lên các mức năng lượng còn trống ở dải dẫn và tham gia vào quá trình dẫn điện giống như các kim loại kiềm. E Dải dẫn Dải cấm Dải hoá trị Hình 9: Cấu trúc dải năng luợng của kim loại kiềm thổ 1.6. Hiện tượng ở chổ tiếp xúc giữa các kim loại. Khi hai kim loại khác nhau tiếp xúc với nhau thì sẽ xuất hiện một hiệu điện thế giữa chúng, hiệu điện thế này đuợc gọi là hiệu điện thế tiếp xúc. Hiệu điện thế tiếp xúc phụ thuộc vào bản chất của hai kim loại, chổ hiệu điện thế giữa hai kim loại đuợc gọi là mối hàn. Nguyên nhân làm xuất hiện hiệu điện thế tiếp xúc này đuợc giải thích như sau, Ở cùng nhiệt độ, hai kim loại khác nhau đuợc tiếp xúc với nhau thì các electron dẫn do chuyển động nhiệt sẽ khuyết tán từ kim loại 1 sang kim loại 2 và ngược lại. Vì mật độ các electron trong kim loại khác nhau, cho nên các dòng electron khuyết tán khác nhau. Gỉa sử mật độ electron dẫn trong kim loại 1 là n1 lớn hơn mật độ n2 của electron dẫn trong trong kim loại 2. Do đó dòng electron khuếch tán của kim loại 1 lớn hơn dòng khuếch tán ngược lại từ kim loại 2 làm cho kim loại 1 sẽ tích điện dương còn kim loại 2 tích điện âm. Giữa hai kim loại xuất hiện một 16 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương điện trường hướng từ kim loại 1 sang kim loại 2. Điện trường này cản trở sự khuyết tán của electron từ kim loại 1 sang kim loại 2 nhưng nó lại thúc đẩy electron từ kim loại 2 sang kim loại 1. Khi hai dòng khuếch tán của các electron dẫn cân bằng, sẽ tồn tại một hiệu điện thế không đổi giữa 2 kim loại. Đó là hiệu điện thế tiếp xúc trong giữa hai kim loại U i (hình 10). + - W      eU i x Hình 10: Biểu đồ phân bố năng lượng ở lóp tiếp xúc giữa hai kim loại. Quá trình trao đổi elelectron giữa hai kim loại xảy ra rất nhanh do tôc sđộ chuyển động nhệt của các electron rất lớn. 17 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương Chuơng II: Ứng dụng của kim loại. 2.1. Ứng dụng của hiện tượng nhiệt điện. Năm 1821, nhà vật lí Thomas Seebeck (1770-1831) đã phát hiện ra hiện tượng nhiết điện (hiện tượng Seebeck). Ở cùng nhiệt độ, một mạch kín gồm hai kim loại khác nhau, trong mạch không có dòng điện. Nếu nhiệt độ ở hai mối hàn khác nhau sẽ có dòng điện chạy qua trong mạch. Độ chênh lệch nhiệt độ giữa hai mối hàn càng lớn thì nhiệt độ càng lớn. Dòng điện này được gọi là dòng nhiệt điện, suất điện động tạo nên dòng điện gọi là suất điện động gọi là suất điện động nhiết điện. Mạch kín nói trên được gọi là cặp nhiệt điện (hình 11). T2  B + A V - B T1 Hình 11: Hiện tượng Seebeck Khi cho dòng điện qua vật dẫn không đồng chất, ngoài nhiệt lượng Joule - Lenz tỏa ra trong thể tích của vật dẫn, người ta còn quan sát thấy một hiện tượng nhiệt phụ nữa xảy ra ở chổ tiếp xúc giữa hai vật dẫn kim loại khác nhau. Khi có dòng điện qua chổ tiếp xúc giữa hai kim loại thì ở đó sẽ có sự tỏa nhiệt hay hấp thụ nhiệt tùy theo chiều dòng điện. Nó làm cho chổ tiếp xúc hoặc nóng lên hoặc lạnh đi. Hiện tượng nhiệt điện này do Jean Peltier phát minh ra năm 1834. Năm 1854, William Thomson đã phát hiện ra rằng một vật dẫn đồng chất mà có biến thiên nhiệt độ thì khi có dòng điện chạy qua sẽ xuất hiện một nhiệt lượng phụ tỏa ra hay hấp thụ trong vật dẫn, độc lập với nhiệt lượng Joule – Lenz. Lượng nhiệt này bổ sung thêm hoặc hấp thụ bớt đi làm cho nhiệt lượng của vật tăng lên hay giảm đi so với khi chỉ có nhiệt lượng Joule – Lenz. Hiện tượng này được gọi là hiện tượng Thomson. Nguồn gốc của hiện tượng này có liên quan chặc chẽ với các nguyên nhân làm xuất hiện các hiệu ứng nhiệt điện xảy ra tại chỗ tiếp xúc. Thí nghiệm quan sát hiện tượng Thomson đã bố trí như sau: Hai vật dẫn a và b giống nhau, làm bằng cùng một vật liệu được mắc vào một mạch điện. Hai đầu của các vật dẫn được giữ ở các nhiệt độ khác nhau. Khi đó, dọc theo các vật dẫn xuất hiện một biến thiên nhiệt độ nên xuất hiện các dòng nhiệt. Trong vật dẫn b, chiều dòng nhiệt trùng với chiều dòng điện, còn trong vật dẫn a, chiều của hai dòng đó ngược nhau. Trên hai vật dẫn chọn hai điểm a và b sao cho khi chưa có dòng điện, nhiệt độ tại hai điểm đó bằng nhau (hình 12). 18 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương Hình 12: Hiện tượng Thomson Thực nghiệm cho thấy, khi có dòng điện trong mạch, nhiệt độ tại hai điểm đó lại khác nhau. Điều đó chứng tỏ rằng đã có nhiệt lượng phụ ngoài nhiệt lượng Joule – Lenz tỏa ra trong một vật dẫn và bị hấp thụ ở vật dẫn kia. Nhiệt lượng phụ đó gọi là nhiệt lượng Thomson. 2.1.1. Nhiệt kế nhiệt điện. Cặp nhiệt điện dùng để đo các nhiệt độ rất cao hoặc rất thấp mà các nhiệt kế thông thường dùng chất lỏng hây thủy ngân, rượu màu không đo được. Cặp nhiệt điện gồm hai vật dẫn kim loại khác nhau (dây 1 và dây 2) được hàn nối với nhau, một đầu hàn được gọi là đầu nóng. Hai dây kim loại cùng mối hàn nóng ( A ) thường được trong ống sứ cách điện để cách li mọi tiếp xúc ở vùng ngoài mối hàn. Nhằm tránh va đập cơ học, một lớp vỏ bọc kim loại phủ bên ngoài để bảo vệ mối hàn nóng và ống sứ. Để cặp nhiệt điện phản ứng nhanh với nhiệt độ bên ngoài, mối hàn nóng có thể được tiếp xúc với lớp vỏ kim loại (hình 13). Hình 13: Sơ đồ sử dụng cặp nhiệt điện đo nhiệt độ Hai vật dẫn cùng có biến thiên nhiệt độ dẫn đến xuất hiện hiệu điện thế nhiệt điện giữa hai mối hàn được tăng cường. Hiệu điện thế này phụ thuộc vào bản chất của kim loại tạo thành cặp nhiệt điện và sự chênh lệch nhiệt độ ở hai mối hàn. Thông thường, mối hàn lạnh ( B ) được giữ ở nhiệt độ không đổi gọi là nhiệt so sánh, nhiệt độ mối hàn nóng ( A ) là nhiệt độ cần xác định. Vì vậy phải biết chính 19 SVTH: Phạm Thị Tiên
Bài tập tiểu luận Huỳnh Trọng Dương xác nhiệt độ so sánh và phải có bản tra cứu chuyển đổi hiệu điện thế nhiệt điện sang nhiệt độ đối với từng loại cặp nhiệt điện được dùng. Các đồng hồ đo nhiệt thường chỉ thị trực tiếp giá trị nhiệt độ của mối hàn nóng. Hiệu điện thế của cặp nhiệt điện nói chung vào khoảng từ 1 đến 70 V , khi sự chênh lệch nhiệt độ của hai mối hàn là một độ. Do cặp nhiệt điện đo hiệu nhiệt độ của hai điểm chứ không chỉ thị nhiệt độ tuyệt đối nên đầu lạnh thường được đặt ở nhiệt độ đã biết trước như nước đá (0 C ) hoặc nhiệt độ phòng. Các cặp nhiệt điện constantan - đồng, constantan - sắt thường được dùng để đo nhiệt độ không cao lắm. Để đo các nhiệt độ cac đến 1700 C thì phải dùng cặp nhiệt điện một dây làm bằng platin nguyên chất, còn dây kia làm bằng hợp kim platin có chứa 10% rodi. 2.1.2. Pin nhiệt điện. Mỗi cặp nhiệt cung cấp một suất điện động nhiệt điện rất nhỏ. Nhiều cặp nhiệt điện mắc nối tiếp nhau có thể tạo thành một bộ pin có khả năng cho suất điện động khoảng vài vôn (hình 14). 1 2 4 6 8 1 3 5 7 9 2 Hình 14: Sơ đồ các cặp pin nhiệt điện Các mối hàn chẵn 2, 4, 6, 8 được đặt ở nhiệt độ T1 còn các mối hàn lẻ 1, 3, 5, 7, 9 đặt ở nhiệt độ T2. Hiệu suất của pin nhiệt điện rất thấp, chỉ khoảng 0,1% nên không có hiệu quả kinh tế. Pin nhiệt điện được làm bằng hai thanh bán dẫn khác loại (bán dẫn loại p và bán dẫn loại n) có hệ số nhiệt điện động  T lớn hơn, hiệu suất cao hơn. 2.1.3. Máy lạnh sử dụng hiệu ứng nhiệt điện Ứng dụng hiện tượng Peltier, người ta thiết kế một linh kiện gồm hai vật dẫn khác nhau có hai mối hàn tạo thành mạch điện. Khi cho dòng điện chạy qua, một mối hàn nóng lên còn mối hàn kia lạnh đi. Điều đó có nghĩa là ta có thể chế tạo được linh kiện có hai mặt, một mặt lạnh chuyển nhiệt sang mặt nóng. Linh kiện này được sử dụng trong các thiết bị đo ở nhiệt độ thấp. Để hiệu suất hoạt động của thiết bị làm lạnh theo nguyên lí của hiện tượng Peltier cao hơn, người ta thấy hai vật dẫn kim loại khác nhau bằng hai tấm dẫn khác loại, bán dẫn loại p và bán dẫn loại n 2.2. Ứng dụng của siêu dẫn để tạo tàu chạy trên đệm từ 20 SVTH: Phạm Thị Tiên

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.26: Bộ 320 Luận Văn Thạc Sĩ Y Học

320 tài liệu

1253 lượt tải

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.