ET 2060 Khái niệm cơ bản về tín hiệu và hệ thống ( TS. Đặng Quang Hiếu )

Chia sẻ: Nguyễn Ngọc Minh | Ngày: | Loại File: PDF | Số trang:10

Thêm vào BST

Báo xấu

174
lượt xem 26
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tín hiệu hàm mũ thực x(t) = Ce at , x[n] = Ce an , 4 3 2 1 0 4 3 2 1 0 0 10 20 30 40 0 1 2 3 −n/10 x[n] = 3e 4 x(t) = 3e −2t 80 60 40 20 0 80 60 40 20 0 0 10 20 30 40 0 1 2 x[n] = e n/10 3 4 C, a ∈ R x(t) = e t Ví dụ: Xét mạch điện có tụ C và điện trở R mắc nối tiếp. Vẽ điện áp v (t) trên tụ C , nếu ban đầu (t = 0)...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: ET 2060 Khái niệm cơ bản về tín hiệu và hệ thống ( TS. Đặng Quang Hiếu )

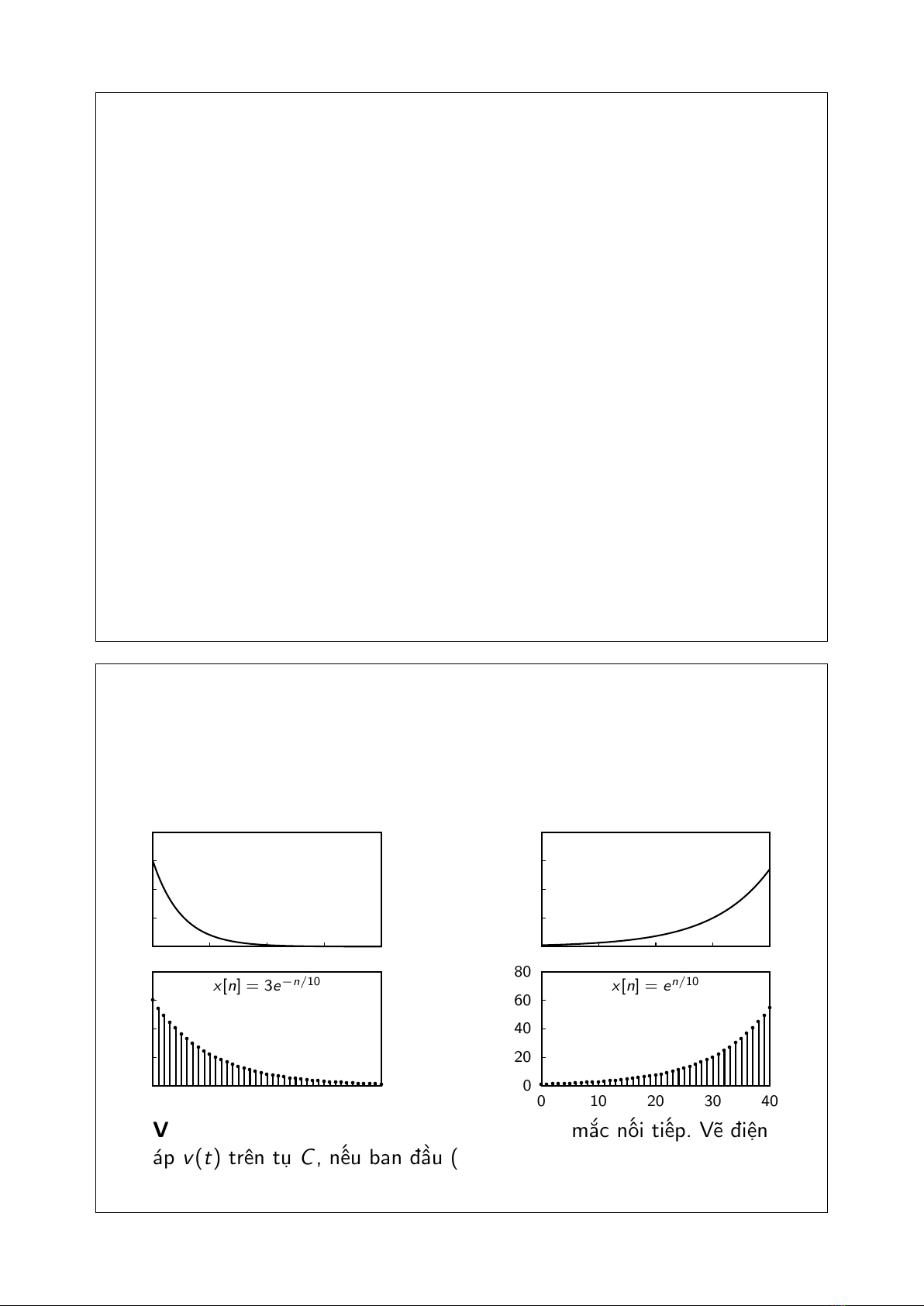
ET 2060 Khái niệm cơ bản về tín hiệu và hệ thống TS. Đặng Quang Hiếu http://ss.edabk.org Trường Đại học Bách Khoa Hà Nội Viện Điện tử - Viễn thông 2011-2012 Tín hiệu hàm mũ thực x (t ) = Ce at , x [n] = Ce an , C, a ∈ R 4 80 x (t ) = e t x (t ) = 3e −2t 3 60 2 40 1 20 0 0 0 1 2 3 4 0 1 2 3 4 4 80 −n/10 e n/10 x [n] = 3e x [n] = 3 60 2 40 1 20 0 0 0 10 20 30 40 0 10 20 30 40 Ví dụ: Xét mạch điện có tụ C và điện trở R mắc nối tiếp. Vẽ điện áp v (t ) trên tụ C , nếu ban đầu (t = 0) tụ được nạp điện V0 .
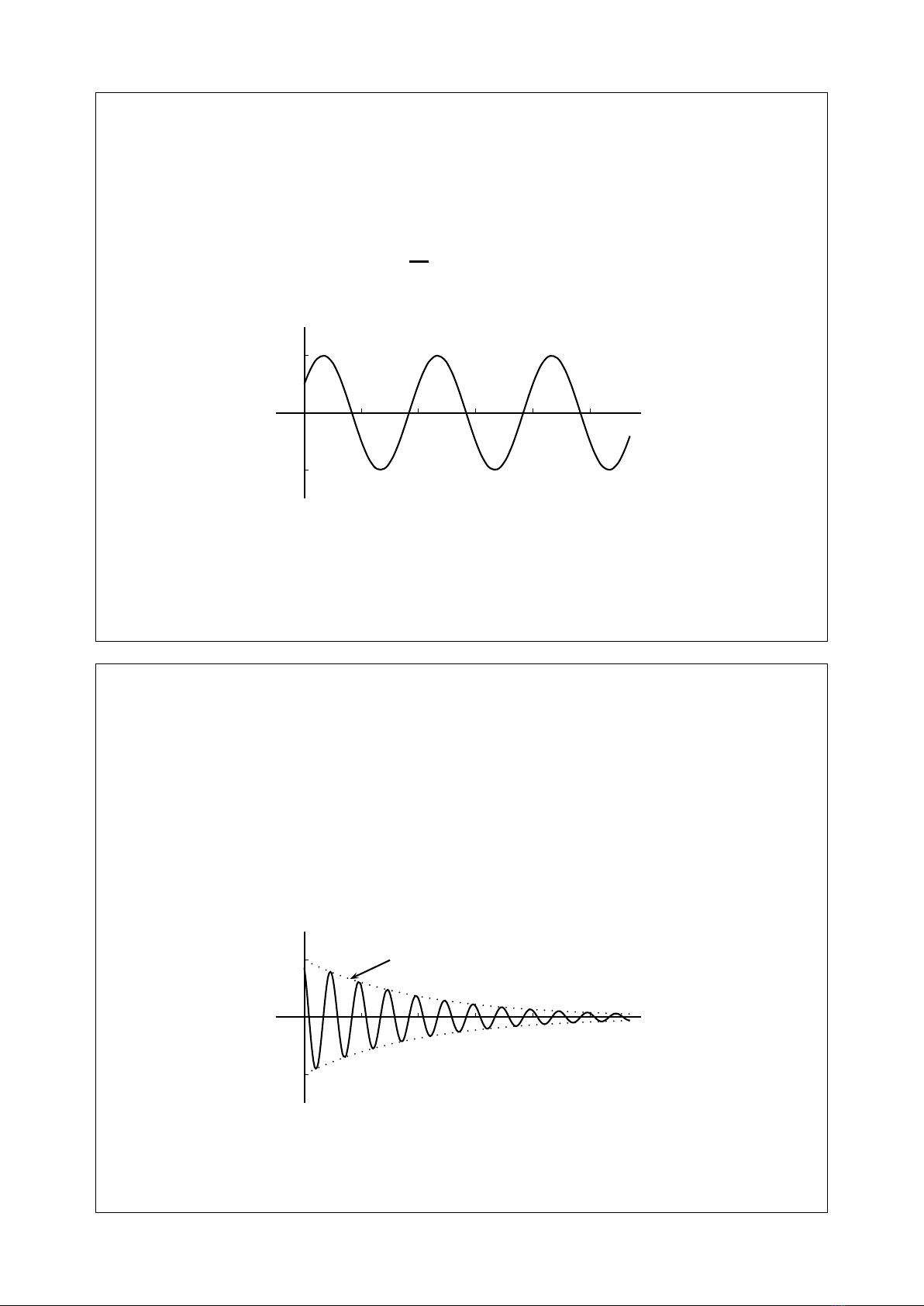
Tín hiệu hình sin x (t ) = sin(ω0 t + φ) 2π Tuần hoàn với chu kỳ T = ω0 → Tín hiệu rời rạc? x (t ) 1 t 1 2 3 4 5 -1 Ví dụ: Cho mạch điện gồm tụ C và cuộn cảm L mắc nối tiếp. Vẽ điện áp v (t ) trên tụ C , nếu ban đầu (t = 0) tụ được nạp điện V0 . Tín hiệu hàm mũ phức (liên tục) Với C và a là số phức: C = |C |e j θ và a = r + j ω0 , ta có: x (t ) = |C |e rt e j (ω0 t +θ) = |C |e rt cos(ω0 t + θ ) + j |C |e rt sin(ω0 t + θ ) Re{x (t )} đường bao |C |e rt 1 t 1 2 3 4 5 -1 Ví dụ trong mạch điện?
Tín hiệu hàm mũ phức (rời rạc) Với C và a là số phức: C = |C |e j θ và a = r + j ω0 , ta có: x [n] = |C |e rn e j (ω0 n+θ) = |C |e rn cos(ω0 n + θ ) + j |C |e rn sin(ω0 n + θ ) Nhận xét về e j (ω0 n+θ) : ◮ Không phải lúc nào cũng tuần hoàn (tùy theo giá trị của ω0 ), chu kỳ? ◮ Chỉ cần xét ω0 trong đoạn [0, 2π ], khi nào tần số thấp / cao? Minh họa x [n] = e j (ω0 n) Im{x [n]} ω0 = 0.8π 1 n 10 20 30 40 50 -1 Im{x [n]} ω0 = 1.8π 1 n 10 20 30 40 50 -1
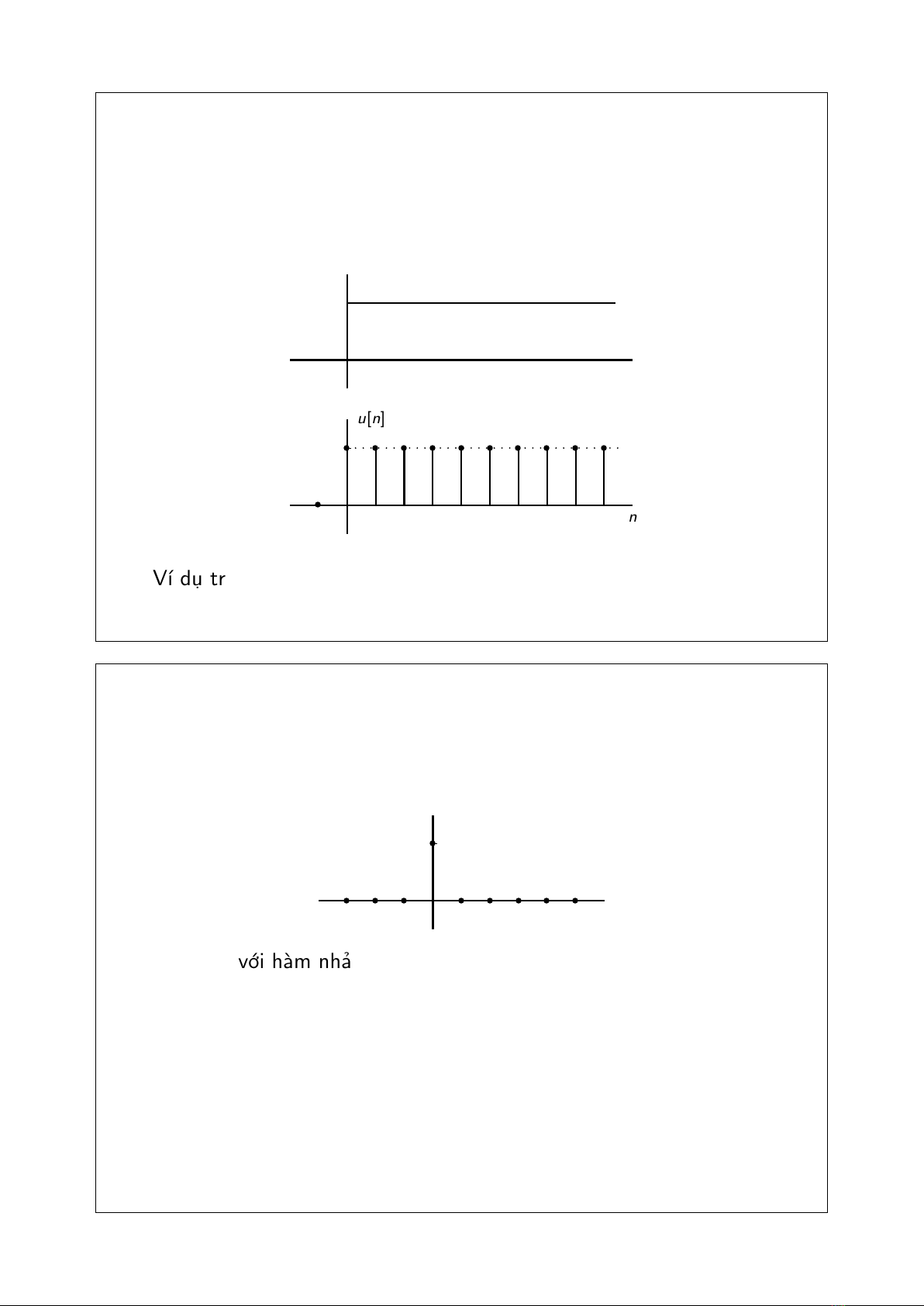
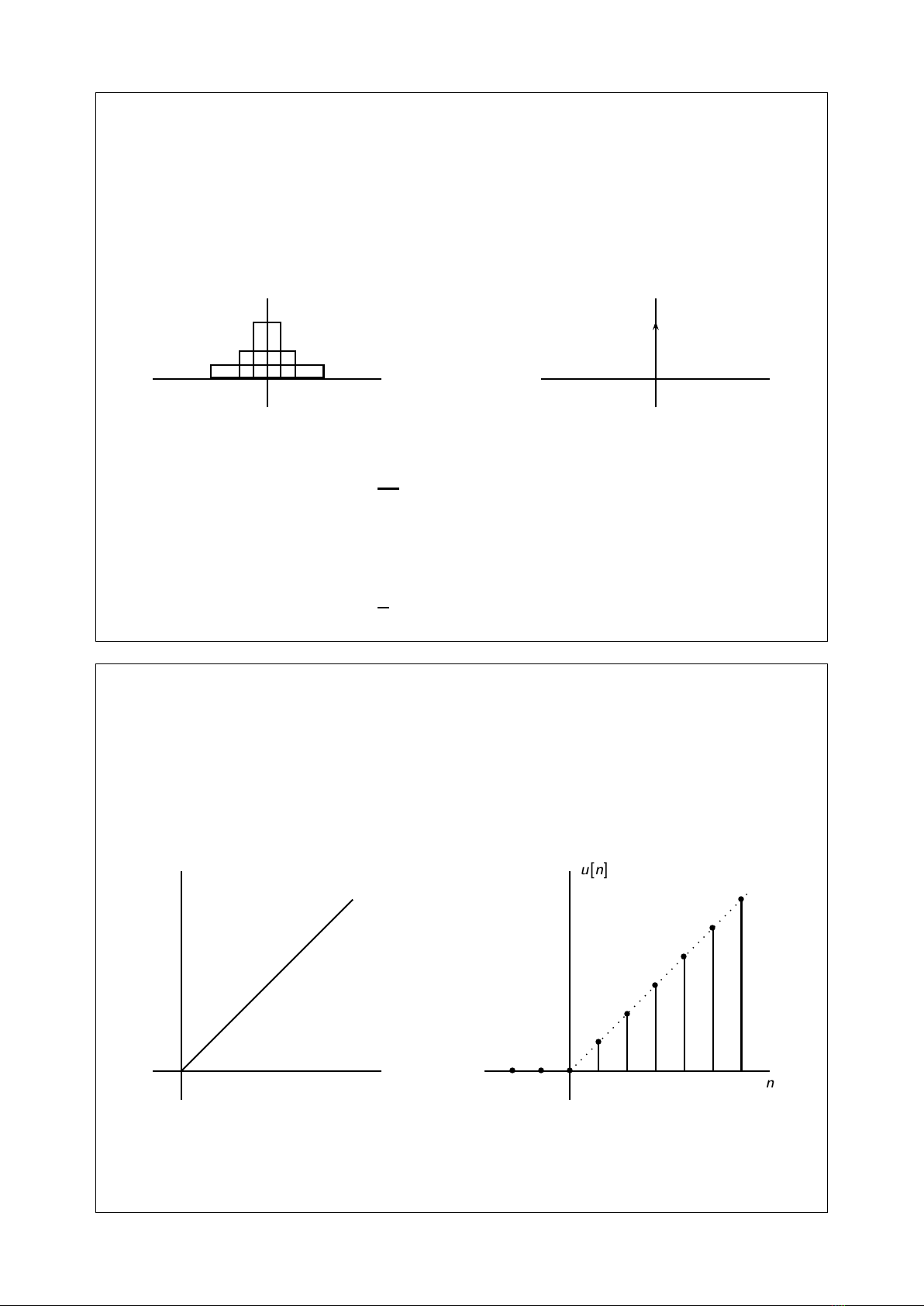
Hàm nhảy đơn vị 1, t ≥ 0 1, n ≥ 0 u (t ) = u [n] = 0, t còn lại 0, n còn lại u (t ) 1 t u [n] 1 n Ví dụ trong mạch điện? Hàm xung đơn vị (rời rạc) 1, n = 0 δ[n] = 0, n còn lại δ [n] 1 n Quan hệ với hàm nhảy đơn vị? δ[n] = u [n] − u [n − 1] ∞ δ[n − k ] u [n] = k =0 Với tín hiệu x [n] bất kỳ? ∞ x [k ]δ[n − k ] x [n] = k =−∞
Hàm delta Dirac (liên tục) ∀t = 0 δ(t ) = 0, ∞ δ(t )dt =1 −∞ x (t ) δ(t ) 1 t t Một số tính chất: t d δ(t ) = u (t ), u (t ) = δ(τ )d τ dt −∞ ∞ x (t )δ(t − t0 )dt x (t0 ) = −∞ 1 δ(at ) = δ(t ) a Hàm dốc đơn vị (ramp) t, t ≥ 0 n, n ≥ 0 r (t ) = r [n] = 0, t còn lại 0, n còn lại u (t ) u [n] n t
Hệ thống T x [n] − y [n] → x (t ) y (t ) hệ thống liên tục x [n] y [n] hệ thống rời rạc Ghép nối các hệ thống đầu vào đầu ra hệ thống 1 hệ thống 2 hệ thống 1 đầu vào đầu ra + hệ thống 2 đầu vào đầu ra + hệ thống 1 hệ thống 2
Tính ổn định của hệ thống Một hệ thống T ổn định (BIBO stable) nếu đầu ra bị chặn |y (t )| < ∞, ∀t khi đầu vào bị chặn |x (t )| < ∞, ∀t Ví dụ: Xét tính ổn định của hệ thống y [n] = r n x [n] với |r | > 1. Thuộc tính nhớ ◮ Hệ thống gọi là không có nhớ (memoryless) nếu đầu ra chỉ phụ thuộc vào đầu vào ở thời điểm hiện tại. ◮ Hệ thống gọi là có nhớ nếu đầu ra phụ thuộc vào đầu vào ở thời điểm quá khứ hoặc tương lai. Ví dụ: Xét thuộc tính nhớ của các hệ thống (a) y [n] = x [n] − x [n − 1] + 2x [n + 2] 1 (b) i (t ) = R v (t )
Tính nhân quả Hệ thống gọi là nhân quả (causal) nếu như đầu ra (thời điểm hiện tại) chỉ phụ thuộc đầu vào thời điểm hiện tại hoặc quá khứ. Ví dụ: Xét tính nhân quả của các hệ thống (a) y [n] = x [n] − x [n − 1] + 2x [n + 2] t 1 (b) i (t ) = −∞ v (τ )d τ L Tính bất biến theo thời gian Hệ thống gọi là bất biến theo thời gian (time invariant) nếu như đầu vào dịch đi một khoảng thời gian thì đầu ra cũng bị dịch thời gian giống hệt như vậy. T T x [n] − y [n] thì → x [n − n0 ] − y [n − n0 ] ∀n, n0 → Ví dụ: Hệ thống sau có bất biến theo thời gian không? y [n] = nx [n]
Tính tuyến tính Hệ thống T gọi là tuyến tính (linear) nếu với các cặp đầu vào / đầu ra: x1 (t ), y1 (t ) và x2 (t ), y2 (t ) thì ta cũng có cặp đầu vào / đầu ra như sau T ax1 (t ) + bx2 (t ) − ay1 (t ) + by2 (t ), → ∀a , b const Ví dụ: Các hệ thống sau có tuyến tính không? (a) y (t ) = tx (t ) (b) y (t ) = x 2 (t ) Tính khả nghịch Một hệ thống gọi là khả nghịch (invertible) nếu như có thể khôi phục được đầu vào từ đầu ra của nó (các đầu vào phân biệt sẽ có các đầu ra phân biệt). x (t ) y (t ) x (t ) T −1 T Ví dụ: Các hệ thống sau có khả nghịch không, nếu có, tìm hệ thống nghịch đảo n (a) y [n] = k =−∞ x [k ] (b) y (t ) = x 2 (t )
Bài tập về nhà ◮ Làm các bài tập cuối chương 1 ◮ Viết chương trình Matlab để vẽ các dạng tín hiệu cơ bản