
Giải tích 2 – Đề số 18
Câu 1: Cho
2 2
2 2
, ( , ) (0,0)
( , )
0, ( , ) (0,0)
x y
xy x y
f x y x y
x y
. Tìm
2 2 2 2
2 2
(0,0), (0,0), (0,0), (0,0)
f f f f
y x x y
x y
.
Bài giải
2 2 2 3 '
2 2 2 2 2 0
( ) 4 ( ,0) (0,0)
' , 0,0 lim 0
( )
x x x
y x y x y f x f
f f x
x y x y
2
20
2
0
' ( ,0) ' ( ,0)
(0,0) lim 0
' (0, ) ' (0,0)
(0,0) lim 1
x x
x
x x
y
f x f x
f
x
x
f y f
f
y x y
2 2 2 3 '
2 2 2 2 2 0
( ) 4 (0, ) (0,0)
' , 0,0 lim 0
( )
y y y
x x y y x f y f
f f y
x y x y
'
2
20
2
0
' (0, ) 0,0
(0,0) lim 0
' ( ,0) ' (0,0)
(0,0) lim 1
y y
y
y y
x
f y f
f
y
y
f x f
f
x y x
Câu 2: . Tìm cực trị của hàm
( , ) 4 6
f x y x y
với điều kiện 2 2
13
x y
.
Bài giải
Xét:
2 2
( , ) 4 6 ( 13)
h x y x y x y
1 2
2 2
' 4 2 0 1 1
' 6 2 0 2 2
3 3
13
x
y
h x
h y P x P x
y y
x y
'' 2 , '' 2 , '' 0
x y xy
h h h
2 2 2
1
2 2 2
2
2 2 0
2 2 0
d h P dx dy
d h P dx dy
Vậy f đạt cực đại P2 và cực tiểu tại P1.
Câu 3: . Tính tổng
1
( 2)
3 1 3 5 (2 1)
n
n
n
Sn
Câu này không giải được. Em nào can đảm thì cứ việc.
Câu 4: Sử dụng khai triển Maclaurint của hàm dưới dấu tích phân thành chuỗi, tính
1
0
1
ln 1
dx
x
Bài giải
Ta có:
1
1
ln ln(1 )
1
n
n
x
x
x n
1 1
1 1
0 0
1 1
ln 1
1 ( 1)
n
n n
x
dx dx
x n n n
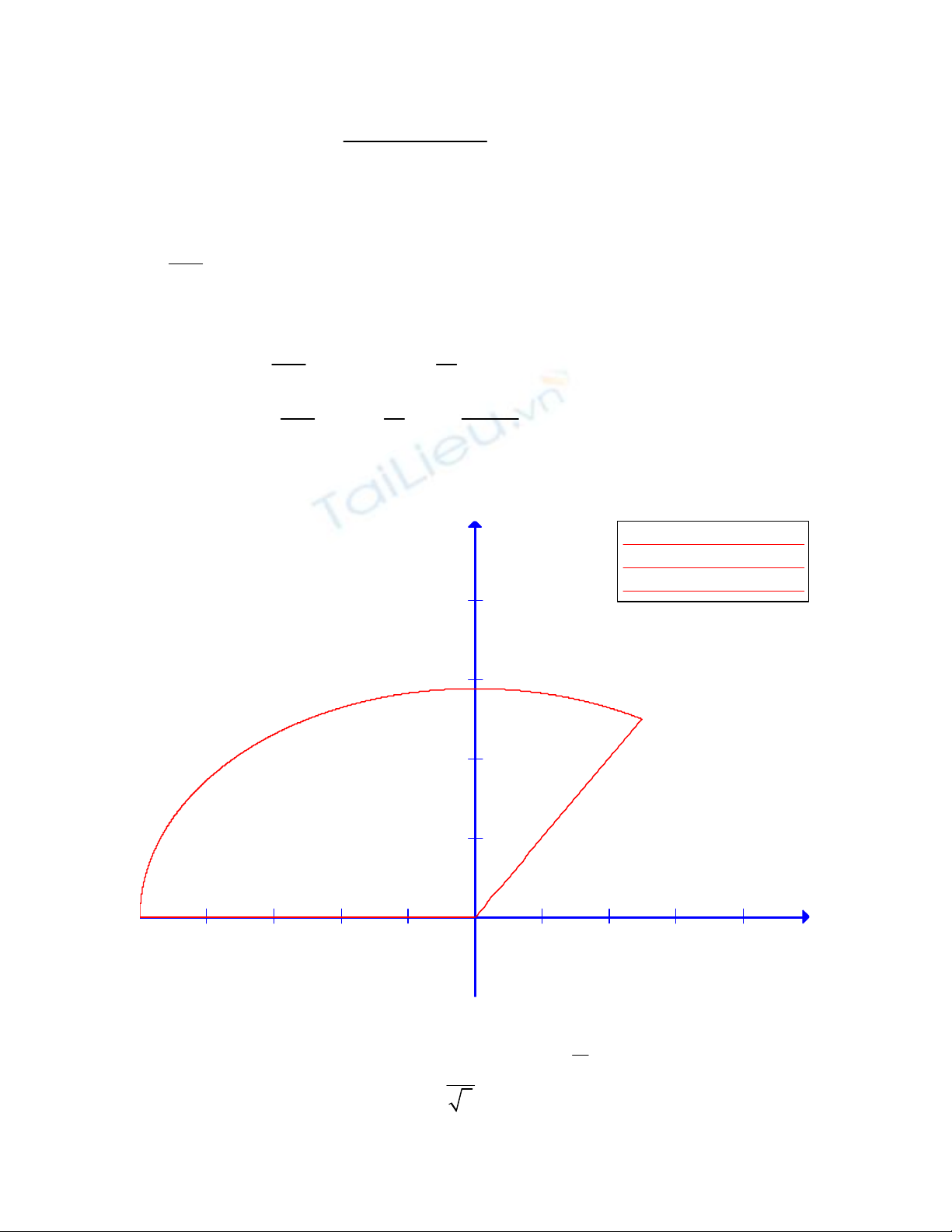
Câu 5: Tìm diện tích miền phẳng giới hạn bởi 2 2
3 1, 0,
x y y y x
.
Bài giải
x(t)=cos(t) , y(t)=1/sqrt(3)*sin(t)
f(x)=x
f(x)=0
-0.8 -0.6 -0.4 -0.2 0.2 0.4 0.6 0.8
0.2
0.4
0.6
0.8
x
y
Trên là diện tích cần tìm:
Đổi sang toạ độ cực mở rộng:
cos
31 sin
0 1
3
x r
y r r

(Để tìm cận dưới của
, ta cho x=y suy ra tan
=
3
. r trong toạ độ cực mở
rộng của Elip luôn đi từ 0 đến 1).
1
0
3
3 3 3
D
r
S dxdy d dr
Câu 6: Tính tích phân
3 2xy xy
C
I x ye dx y xe dy
, trong đó C là phần elip
2 2
1
16 9
x y
từ
Bài giải
Ta có:
1
xy
P Q
xy e
y x
do đó tích phân không phụ thuộc vào đường đi:
0 3
3 2
4 0
64 9 73
CAO OB
I x dx y dy
Câu 7: Tính tích phân mặt loại hai 3
( 1) 3 5
S
I x dydz ydzdx zdxdy
, với S là mặt
ngoài của nửa dưới mặt cầu 2 2
2 , 0
2
x y z x z
.
Bài giải
Gọi S’ là mặt trên của hình tròn 2
2
x y x
2 trong mp Oxy
' '
S S S S
I
Trên S’(z=0): dz=0
'
0
S
Áp Dụng O-G trên khối V gh bởi S và S’:
2
'
3 1 8
S S S V
I x dxdydz
2
[3( 1) 3 5)]
V
I x dxdydz
với V là nữa dưới mặt cầu 2 2
2 , 0
2
x y z x z
2 1 2 2 2 2
0 0
2
23 2
0
2
sin 3 sin os 8
8 3 86
sin sin os
3 5 15
d d c d
d c d


























