Ch ng 6ươ
Giải toán trên EXCEL
6.1. Đ I S MA TR NẠ Ố Ậ
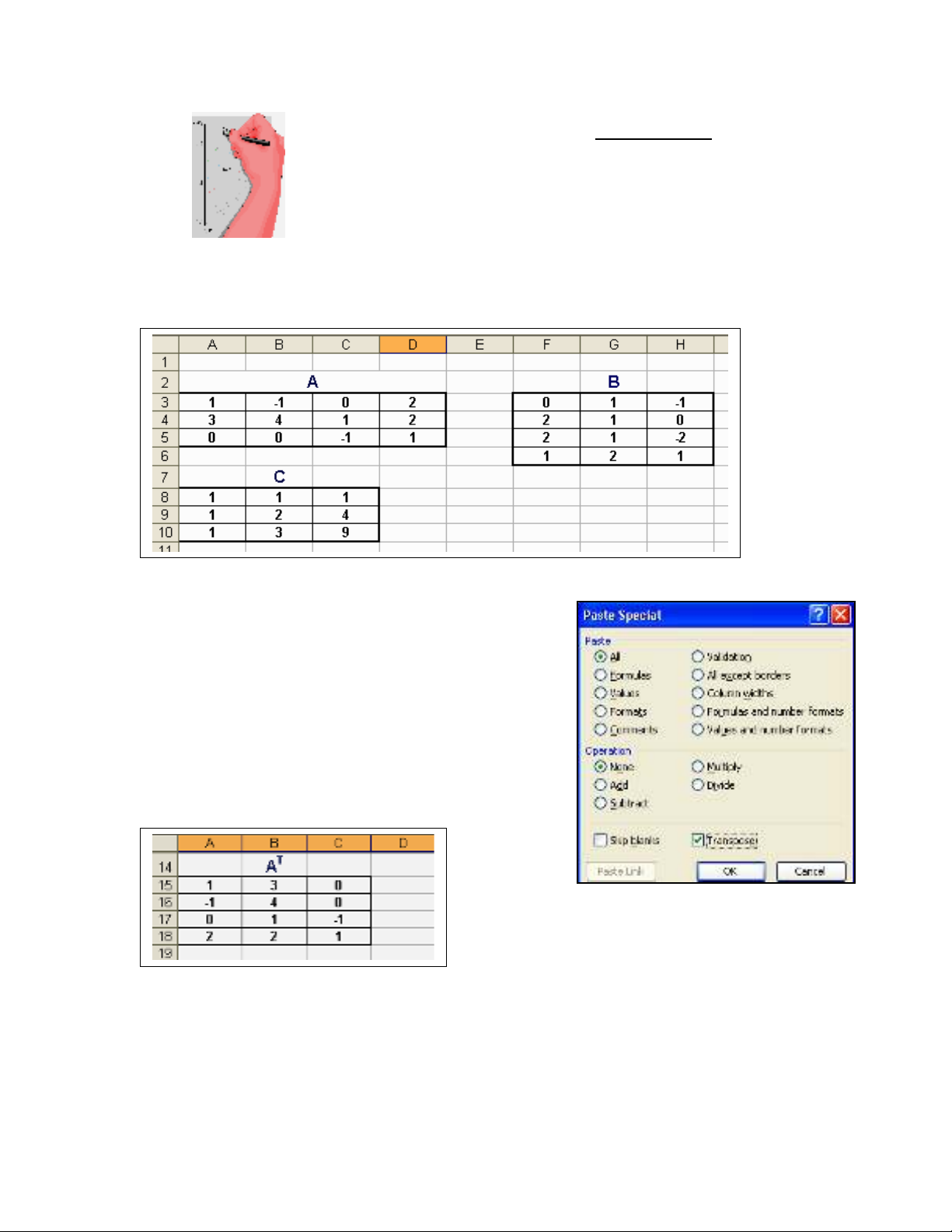
Xét các ma tr n A, B và C b ng tính sau:ậ ở ả
1. L p ma tr n chuy n v (ậ ậ ể ị Transpose Matrix) c a A:ủ AT
Các b c th c hi n:ướ ự ệ
•Quét ch n kh i ma trọ ố n A (vùng ậA3:D5)
•Th c hi n l nh ự ệ ệ Edit – Copy (ho c gõ ặCtrl+C)
•Ch n v trí l p ma tr n chuy n v (ô ọ ị ậ ậ ể ị A15)
•Dùng l nh ệEdit – Paste Special. Xu t hi n h p tho iấ ệ ộ ạ
•Ch n ọTranspose, và OK.
Ta có k t qu :ế ả
2. L p ma tr n ngh ch đ o ậ ậ ị ả (Inverse Matrix) c a C: Củ-1
Các b c th c hi n:ướ ự ệ
•Ch n v trí l p ma tr n ngh ch đ o (ô ọ ị ậ ậ ị ả A22)
159
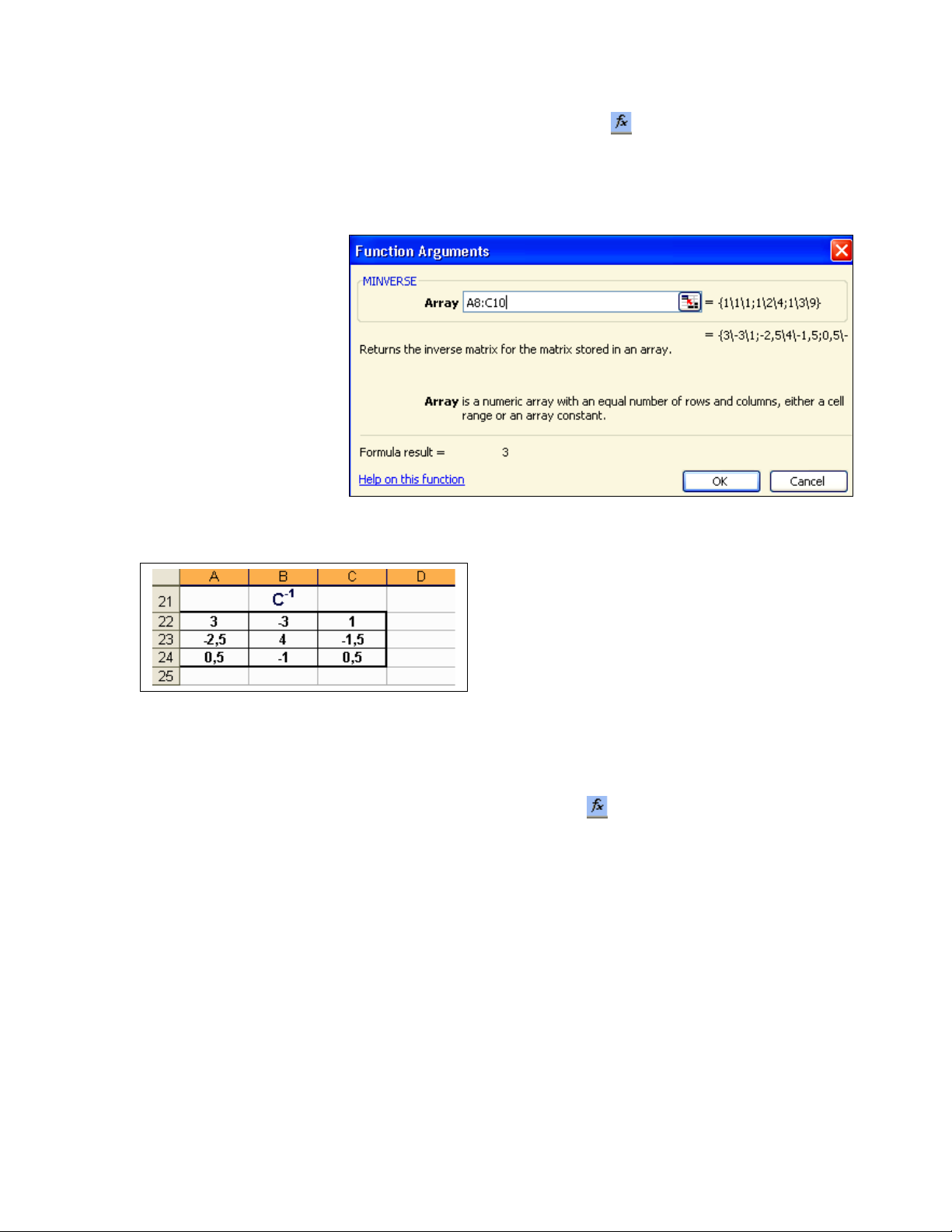
•Dùng l nh ệMINVERSE (ho c ặClick bi u t ng ể ượ trên Toolbar. Ch n ọMath
& Trig, r i ch n l nh ồ ọ ệ Minverse). Xu t hi n h p tho i:ấ ệ ộ ạ
•Ch n vùng xác đ nh ma tr n C (ọ ị ậ A8:C10) trong khung Array.
•Click OK.
L u ýư: Sau khi Click
OK, t i v trí con tr ôạ ị ỏ
hi n hành (ô ệA22) chỉ
xu t hi n s h ng ấ ệ ố ạ ở
dòng 1, c t 1 c a Cộ ủ -1. Để
hi n th toàn b ma tr nể ị ộ ậ
C-1, ta ph i quét ch nả ọ
kh i xu t hi n c a Cố ấ ệ ủ -1(3
dòng và 3 c t), b t đ uộ ắ ầ
t s đ u tiên v a xu từ ố ầ ừ ấ
hi n ( đây ta quét ch nệ ở ọ
kh i ốA22:C24). Ti p đ n gõ ế ế F2, r i th c hi n đ ng th i: ồ ự ệ ồ ờ Ctrl + Shift + Enter.
Ta có k t qu :ế ả
3. Nhân (multiply) hai ma tr n A và B: A.Bậ
Các b c th c hi n:ướ ự ệ
•Ch n v trí l p ma tr n tích (ô Aọ ị ậ ậ 27)
•Dùng l nh ệMMULT (ho c ặClick bi u t ng ể ượ trên Toolbar. Ch n ọMath &
Trig, r i ch n l nh ồ ọ ệ MMULT). Xu t hi n h p tho i:ấ ệ ộ ạ
160
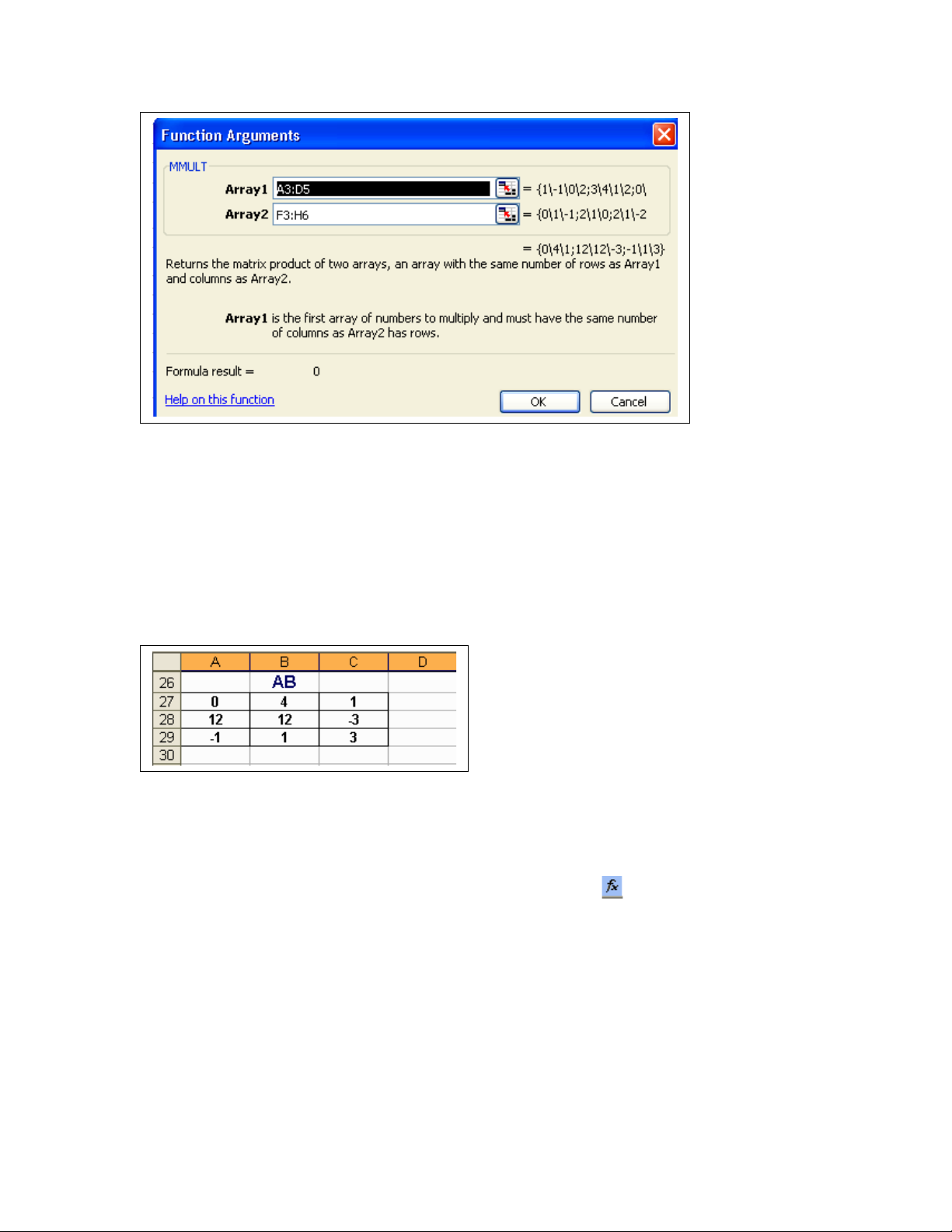
•Ch n vùng xác đ nh ma tr n A (ọ ị ậ A3:D5) trong khung Array1; Ch n vùng xácọ
đ nh ma tr n B (ị ậ F3:H6) trong khung Array2.
•Click OK.
L u ýư: Sau khi Click OK, t i v trí con tr ô hi n hành (ô ạ ị ỏ ệ A27) ch xu t hi n s h ng ỉ ấ ệ ố ạ ở
dòng 1, c t 1 c a ma tr n AB. Đ hi n th toàn b ma tr n AB, ta ph i quét ch n kh iộ ủ ậ ể ể ị ộ ậ ả ọ ố
xu t hi n c a AB (3 dòng và 3 c t, vì A c p 3x3 – B c p 4x3 ), b t đ u t s đ u tiênấ ệ ủ ộ ấ ấ ắ ầ ừ ố ầ
v a xu t hi n. Ti p đ n gõ ừ ấ ệ ế ế F2, r i th c hi n đ ng th i: ồ ự ệ ồ ờ Ctrl + Shift + Enter.
Ta có k t qu :ế ả
4. Tính đ nh th c c a ma tr n ị ứ ủ ậ (Matrix determinant) vuông C: Det C
Các b c th c hi n:ướ ự ệ
•Ch n v trí tính đ nh th c (ô ọ ị ị ứ F9)
•Dùng l nh ệMDETERM (ho c ặClick bi u t ng ể ượ trên Toolbar. Ch n ọMath
& Trig, r i ch n l nh ồ ọ ệ MDETERM). Xu t hi n h p tho i:ấ ệ ộ ạ
161
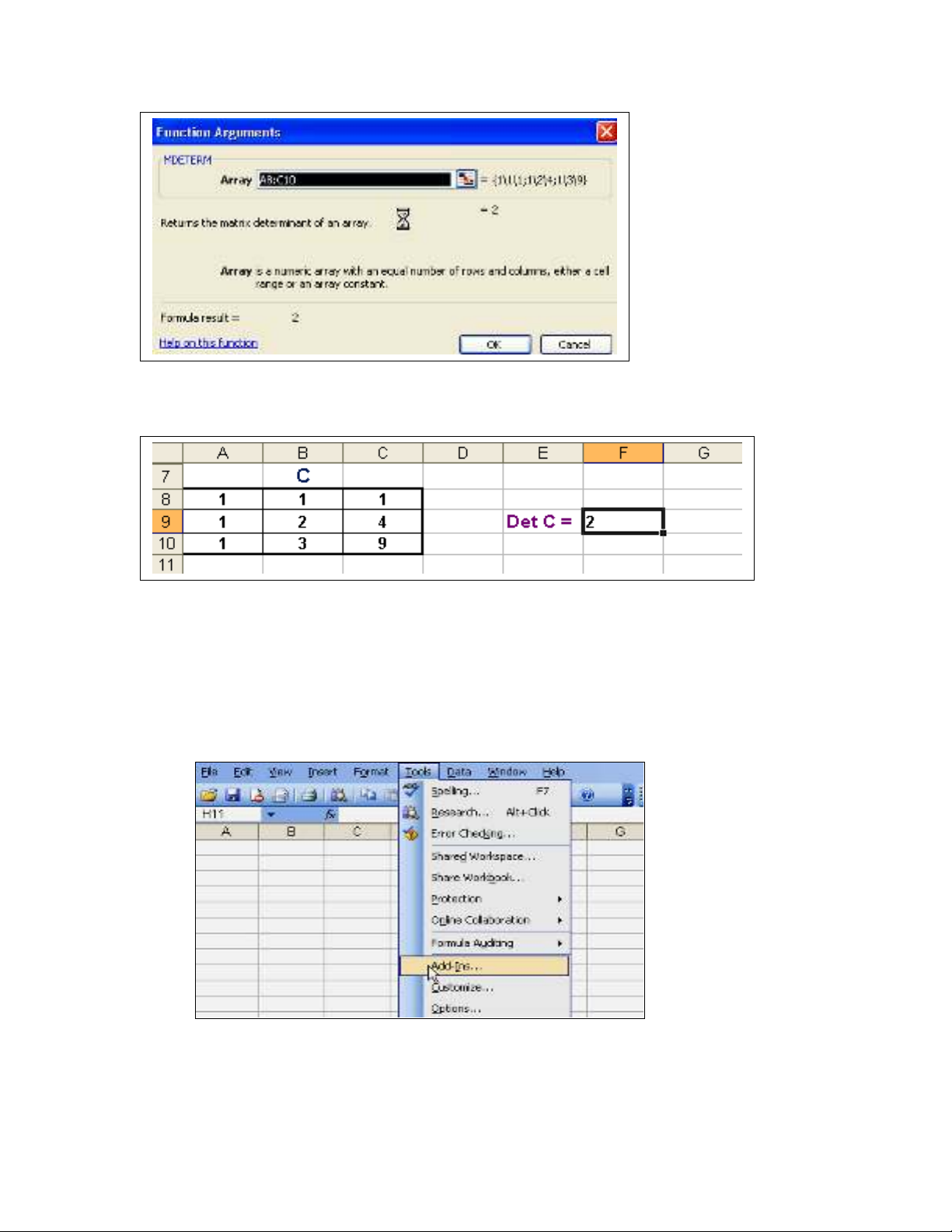
•Ch n vùng xác đ nh ma tr n C (ọ ị ậ A8:C10) trong khung Array.
•Click OK.
6.2. GI I ẢH PH NG TRÌNH TUY N TÍNHỆ ƯƠ Ế
Dùng l nh ệSolver trong Menu Tools c a Excel. N u trong tr ng h p trong ủ ế ườ ợ Menu Tools
ch a có l nh này, ta th c hi n các thao tác sau:ư ệ ự ệ
Dùng l nh: ệTools | Add-Ins…
Xu t hi n hấ ệ p tho i Add-Ins:ộ ạ
162
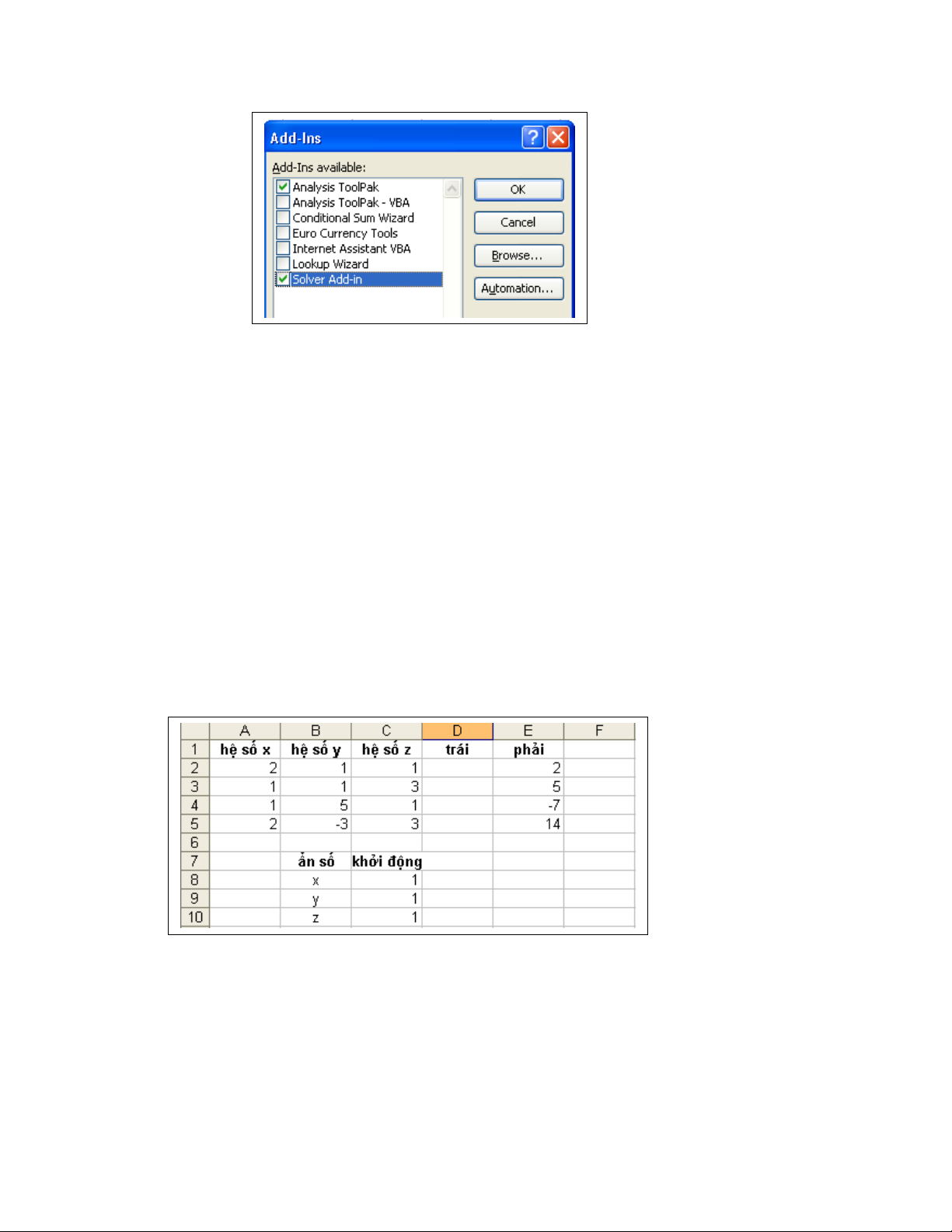
•Click ch n m c ọ ụ Solver Add-in.
•Click nút OK.
Trong Menu Tools s xu t hi n l nh Solver.ẽ ấ ệ ệ
Ví d : ụGi i hả ph ng trình tuy n tính:ệ ươ ế
=+−
−=++
=++
=++
14332
75
53
22
zyx
zyx
zyx
zyx
a) Trình bày bài toán trên b ng tính Excel:ả
•A1:E1 và B7:C7 là dòng tiêu đ .ề
•A2:A5 là các h s c a x; B2:B5 là các h s c a y, C2:C5 là các h s c a z.ệ ố ủ ệ ố ủ ệ ố ủ
•B8:B10 là tên các n s .ẩ ố
•C8:C10 là giá tr ban đ u c a n s . Sau khi gi i xong, vùng này là nghi m c aị ầ ủ ẩ ố ả ệ ủ
ph ng trình t ng ng v i các n s .ươ ươ ứ ớ ẩ ố
•C t ộtrái đ tr ng.ể ố
163