Ch
Chæå
æång
ng 8:
8: N
Näú
äúi
iâ
âáú
áút
ttrong
trong hã
hãûûth
thäú
äúng
ng âiã
âiãûûn
n
I) Khaïiniãûmchung:
Nhiãûnvuûcuíanäúiâáútlaìâãøtaíndoìngâiãûnvaìoâáútvaìâãøgiæîmæïcâiãûnthãútháúptrãncaïcváûtdæåücnäúiâáút
TrongHTÂ chuïngtacoïcaïcloaûinäúiâáútsauâáy:
-Näúiâáútan toaìn: nhàòmâaímbaíoan toaìnchocon ngæåìi, näúitáútcaícaïcbäüpháûn
kimloaûicuíaTBÂ hay cuíacaïckãútcáúukimloaûimaìkhicaïchâiãûnbëhæhoíngthç
noïxuáúthiãûnâiãûnaïpxuäúnghãûthäúngnäúiâáút.
-Näúiâáútchäúngseït : âaímbaíoan toaìnchoTBÂ laìchênh. Näúitæìbäüpháûnthuseït
Caí2 loaûinäúiâáúttrãnâæåücgoüilaìnäúiâáútbaíovãû
-Näúiâáútlaìmviãûc : nhàòmâaímbaíoâiãöukiãûnlaìmviãûcbçnhthæåìngchoTBÂ vaì
1 säúbäüpháûncuíaTBÂ theochãúâäüâaîâæåücqui âënhsàôn
II) Hãûsäúmuìa:
Âáútlaìmäitræåìngdáùnâiãûnphuûthuoüocvaìoráútnhiãöuyãúutäú:
-Læåüngáømtrongâáút.
-Nànglæûcgiæîáømcuíaâáút
Tæïclaìphuûthuäücvaìokêchthæåïchaûtâáút: haûtcaìngmëncaìngtäút
âáútgiæîáømcaìngtäútthçlaìâáúttäút
-Taûpcháúttrongâáút
Vçváûykhitênhtoaïnnäúiâáútthçngæåìitaláúy muadott k.ρρ =
Kmuìa thoaímaîncaí4 muìa
* KhiâovaìomuìamæathçnhánvåïiK
muìa låïndo nhoí
ρ
KhiâovaìomuìanàõngthçnhánvåïiK
muìa nhoído lớn
ρ
* Kmuìa phuûthuäücvaìoâäüchänsáucuíaâiãûncæûc
* Kmuìa phuûthuäücvaìoloaûinäúiâáút: näúiâáútchäúngseït
láúyk
muìa nhoíhånso våïinäúiâáútan toaìn
III) Tênhtoaïnnäúiâáútan toaìn:
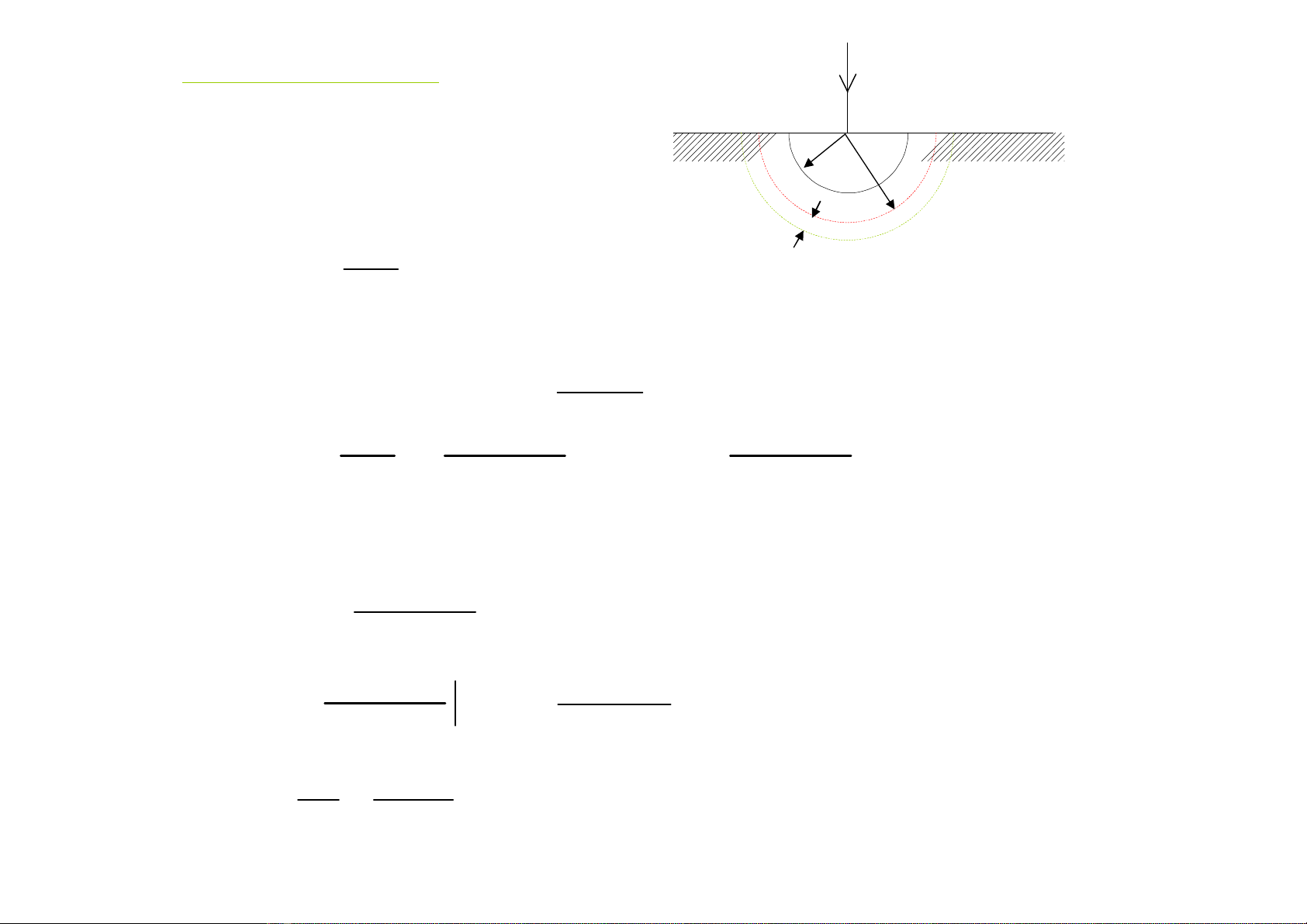
1)Xaïc âënhâiãûntråínäúiâáútcuíacaïcâiãûncæûcâån: I
â
rr
o
dr
Khinäúiâáútan toaìncoïI
â= INM 1 pha
Iâ=Ichaûmâáút
ρ.J
dr
du
E==
_máûtâäüdoìngâiãûnâitrongâáút
J
_âiãûntråísuáútcuíaâáút
ρ
XaïcâënhR
nâ ta
xuáútphaïttæìâënhluáûtOhm daûngvi phán
2
2r
I
Jd
∏
=
Xeït1màût cáöubaïnkênhr báútkyìtacoï:
dr
r
I
du
r
I
dr
du
Edd
22 2
.
2
.
∏
=⇒
∏
==
ρ
ρ
α
ϕϕ −= roro
u
Âiãûnaïptrãnbãömàûtbaïncáöur
o
:
∝
∏
−
=
∏
=∫
ro
d
ro
d
r
I
dr
r
I
2
.
2
.
2
ρ
ρ
α
o
d
r
I
∏
=2
.
ρ
od
ro
bc rI
u
R∏
== 2
ρ
Âiãûntråínäúiâáútcuíabaïncáöur
o
:
mm )8,05,0(
÷
=
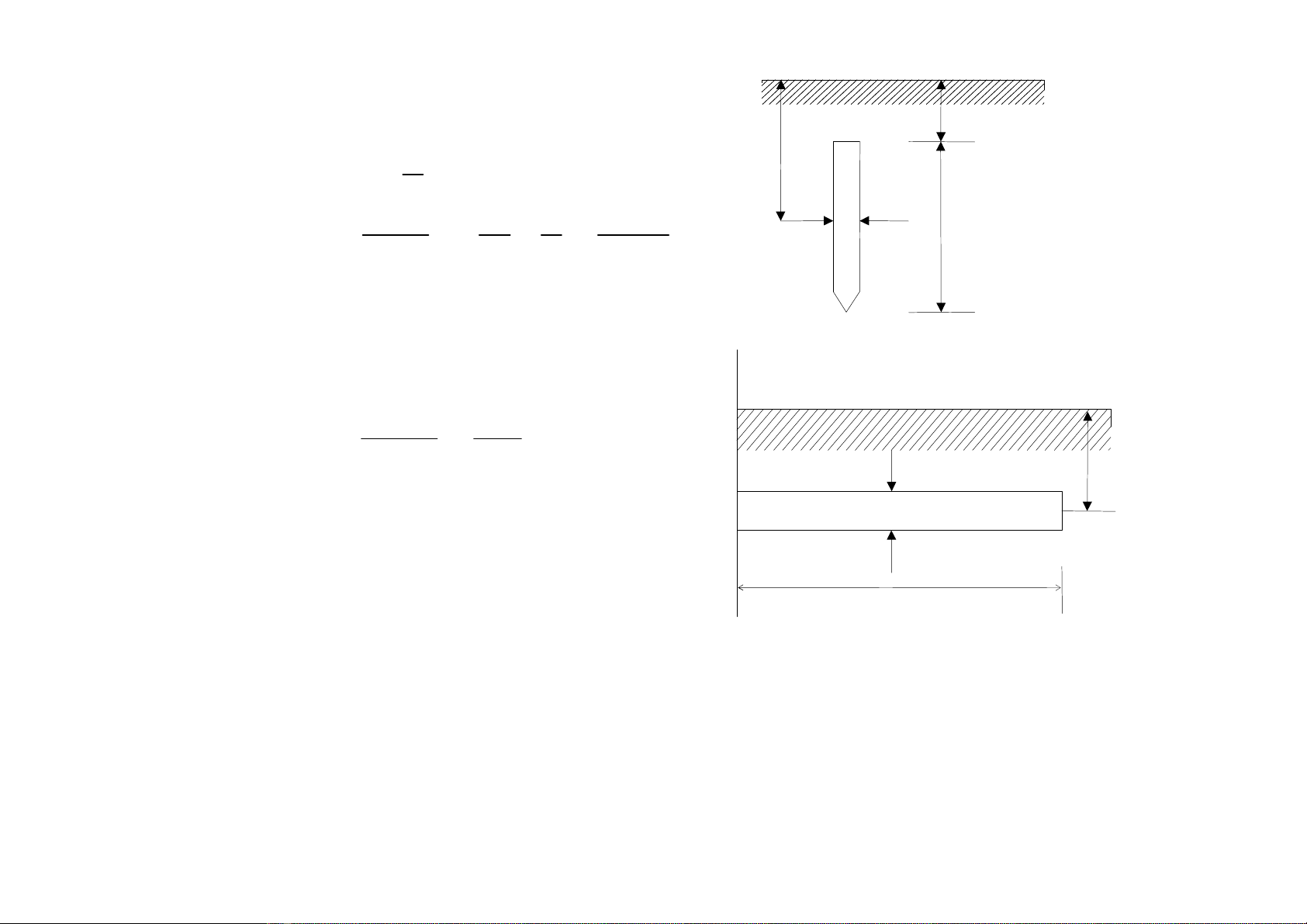
*Âiãûntråínäúiâáútcuíacoücchänsáutrongâáút:
2
l
mt +=
−
+
+
∏
=lt
lt
d
l
l
Rtt
c4
4
ln
2
12
ln
2
ρ
cmd )52(
÷
=
ml )32(
÷
=
t
l
m
d
*Âiãûntråínäúiâáútcuíathanhchännàòmngang:
dt
kL
L
Rtt
c.
ln
2
2
∏
=ρ
cmd )32(
÷
=
L
t
d
K_hãûsäúphuûthuäücvaìohçnhdaïngnäúiâáút
T_âäüchänsáu
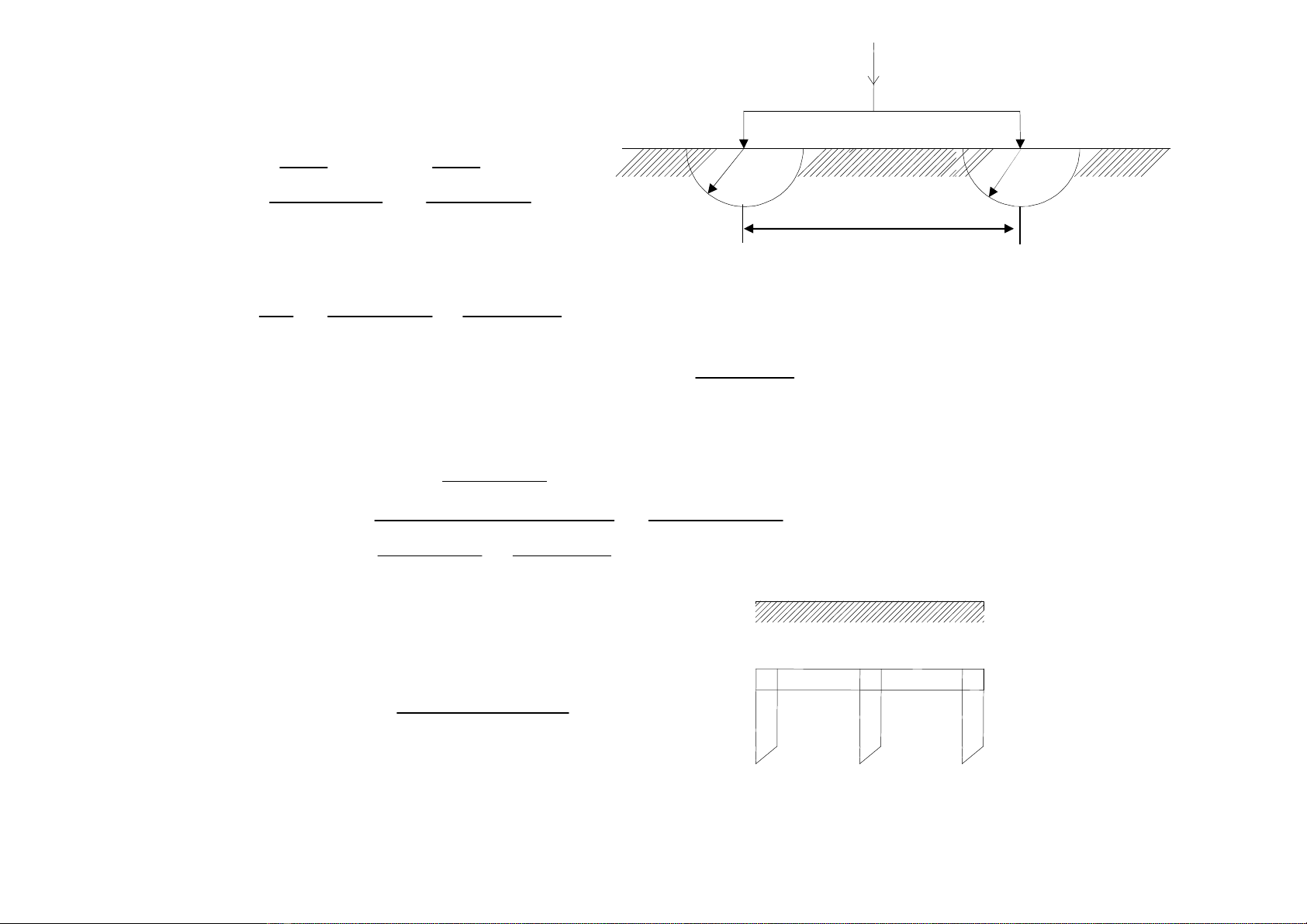
2)Xaïc âënhâiãûntråínäúiâáútcuía1 hãûthäúng:
Xeïtâiãûncæûcgäöm2 baïncáöubaïnkênhr
o
I
d
I
d
/2 Id/2
roro
a
a
I
r
I
u
d
o
d
∏
+
∏
=2
.
2
2
.
2
1
ρρ
arI
u
R
od
bc ∏
+
∏
== 2.22.2
1
2
ρ
ρ
Âiãûntråínäúiâáútcuíahãûthäúng:
Khixeïtâãúnaínhhæåíngláùnnhaugiæîa2 âiãûncæûccoïthãm so våïitræåìnghåüplyïtæåíng
a∏2.2
ρ
Âãøâàûctrængchohiãûntåüngnaìythçngæåìitaâæara1 hãûsäúgoüilaìhãûsäúsæíduûng
η
ar
r
ar
r
o
o
o
o
/1/1
/1
2.22.2
2.2
+
=
∏
+
∏
∏
=ρρ
ρ
η
1
<
η
* n coücliãnkãútvåïinhaubàòngthanhchännàòmngang
nRR
RR
R
cttc
tc
ht .
.
ηη +
=
IV) Tênhtoaïnnäúiâáútchäúngseït:
1) Âàûcâiãøm:
-Doìngâiãûnseïtcoïbiãnâäülåïn(Islåïn) tæïcmáûtâäüJ låïn, suyraE låïn
NãúuE >Ecpâ thçvuìngâáútxungquanhâiãûncæûcseîbëphoïngâiãûn, luïcnaìytæångâæångvåïikêchthæåïccuía
âiãûncæûctànglaìmgiaímâaïngkãøtrësäúâiãûntråínäúiâáút
-Do låïndo âoïkhängthãøboíqua aínhhæåíngcuíaâiãûncaímcuíabaínthánâiãûncæûc. Båíivçnoï
gáyra1 âiãûnaïpgiaïng trãnbaínthánâiãûncæûc.
di
as
=
Lúc này hãûthäúngnäúiâáútkhängthuáöntuyïnhæ1 âiãûntråínæîamaìlaìtäøngtråíZ vaìlaìmtrësäúOhm tànglãnkhaïlåïn
Khil >40 m thçluïcâoïmåïixeïtaínhhæåíngcuíaâiãûncaím
ρ
Khidoìngâiãûnseïtâivaìoâáútlaìmcho thayâäøi, tacoïcängthæïc
di
Ls
)1( rxk kE−= ρρ
)05,001,0(
÷
=
k
2) Phánloaûi:
-Näúiâáúttáûptrung: khichiãöudaìicuíaâiãûncæûcchänvaìotrongâáútl < 40 m
Boíqua aínhhæåíngcuíaL chèxeïtdãúnhiãûntæåüngphoïngâiãûnåítrongâáút
-Näúiâáútphánbäúdaìi:
Xeïtâäöngthåìicaí2 aínhhæåíng:
+Hiãûntæåüngphoïngâiãûntrongâáút
+ AÍnhhæåíngcuíaâiãûncaím
Tuynhiãnbaìitoaïnnaìykhaïphæïctaûp, chonãnâäúivåïitræåìnghåüpnay chèxeïtâãúnL boíqua hiãûntæåüngphoïngâiãûn
trongâáút
ml 40
≥