Ch
Chæå
æång
ng 9:
9: Qua
Quaïïtr
trç
çnh
nh so
soïïng
ng trãn
trãn â
âæåì
æåìng
ng d
dá
áy
y
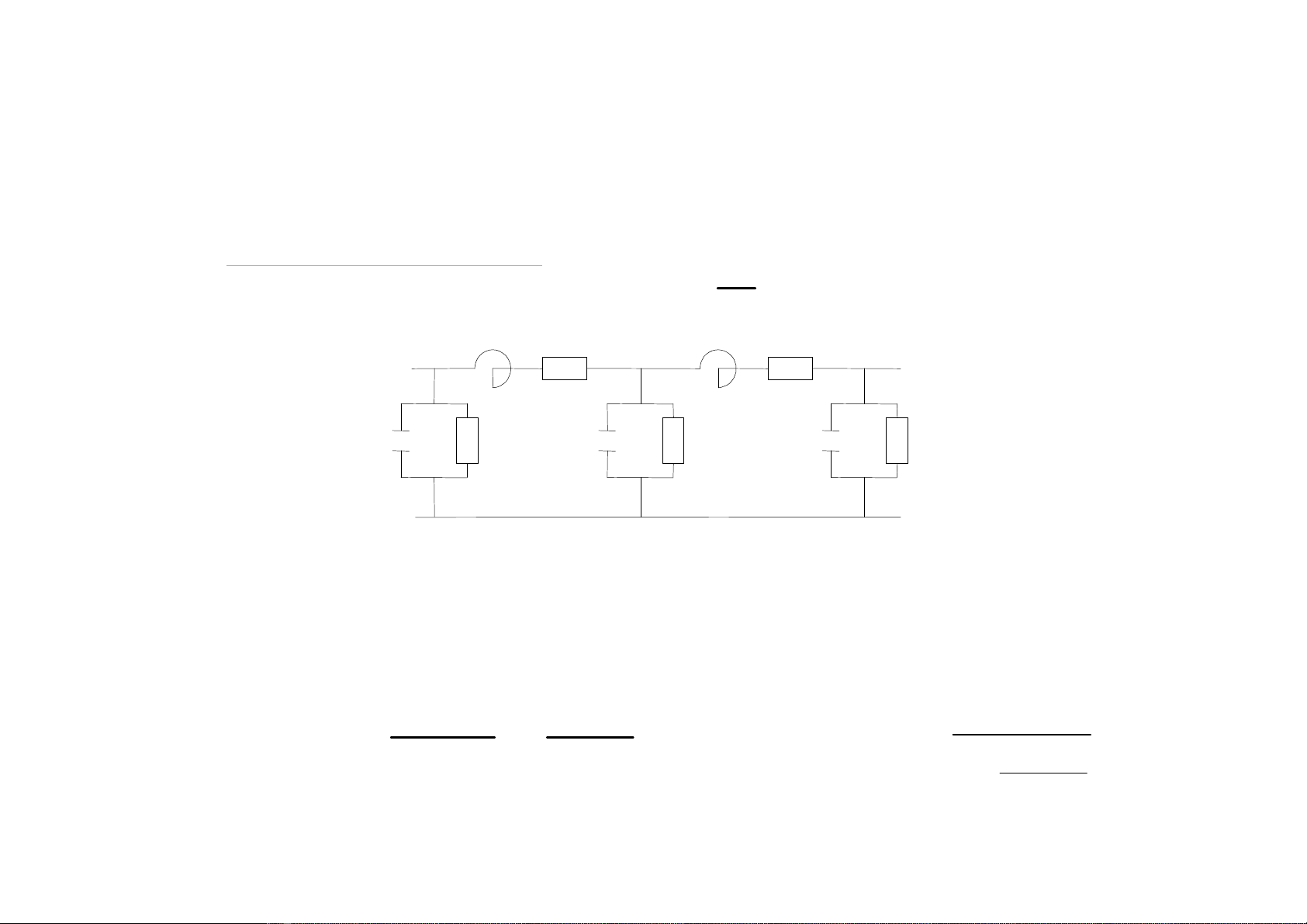
I) Hãûphæångtrçnhtruyãönsoïng:
Âæåìngdáylaì1 pháöntæíchiãúm1 khoaíngkhänggianräünglåïntronghãûthäúngâiãûndo âoïkhaínàngseïtâaïnh
vaìodáydáùnráútlåïn. Khiseïtâaïnhlãnâæåìngdáysaínsinhrasoïngâiãûntæìlantruyãöndoüctheoâæåìngdáyvaìgáy
nãnquaïâiãûnaïptaïcduûngnãncaïchâiãûncuíahãûthäúng, laìmphaïhuyícaïchâiãûn
Såâäöthaythãúcuíaâæåìngdáydaìi:
Trongâoï:
f
c
=λ
R
C
r
h
Ldd
2
ln
2ε
µ
∏
=
G
r
h
C
dd
2
ln
2
ε
∏
=
L_ âiãûncaímtrãn1 âånvëdaìicuíaâæåìngdáy
L
R_ âiãûntråítaïcduûngtrãn1 âånvëdaìicuíaâæåìngdáy
C_ âiãûndung trãn1 âånvëdaìicuíaâæåìngdáyso våïiâáút
G_ âiãûndáùntrãn1 âånvëdaìicuíaâæåìngdáyso våïiâáút
t
i
LRi
x
u
o∂
∂
+=
∂
∂
−
Hãû phæångtrçnhvi phánbiãøudiãùnquaïtrçnhtruyãönsoïngtrãnâæåìngdáy:
t
u
CuG
x
i
o∂
+=
∂
−
Nãúuâæåìngdáykhängcoïtäønhao(R=0, G=0) thitacoï:
t
i
L
x
u
o∂
∂
=
∂
∂
−
t
u
C
x
i
∂
=
∂
∂
−
Nghiãûmtäøngquaïtcuíahãûphæångtrçnhtrãndæåïidaûngsoïngchaûynhæsau:
)()( 21 vtxfvtxfu ++−=
[ ]
)()(
1
21 vtxfvtxf
Z
i+−−=
Phæångtrçnhtrãnla phæångtrçnhtruyãönsoïngkhängcoïtäønhao
Trongâoï: f1_ thaìnhpháönsoïngtåïi
f2_ thaìnhpháönsoïngphaínxaû
mF /
10.9.4
1
9
∏
=ε
mH /10.4 7−
∏=µ
Våïi: sm
c
LC
v/10.3
18
≈== µε
)400( Ω<= C
L
Z
: váûntäúctruyãönsoïng
: täøngtråísoïng
II) Truyãönsoïnggiæîa2 mäitræåìng:
Giaísæícoï1 soïngtåïiu
tlantruyãöntrongmäitræåìngcoïtäøngtråísoïnglaìZ
1
Z
1u
f
M
u
t
Z
2
u
k
ÂãúnâiãømM noïchuyãønsang mäitræåìngcoïtäøngtråísoïnglaìZ
2
.
Khisoïngtruyãönsang mäitræåìngmåïithçnoïseîxuáúthiãûnthaìnhpháönsoïng
khuïcxaûu
kâäöngthåìicoïthaìnhpháönsoïngphaínxaûu
fvãömooitræåìngcuî
PhæångtrçnhâiãöukiãûnbåìtaûiM:
ut+ uf= uk(1)
It -I
f= Ik(2)
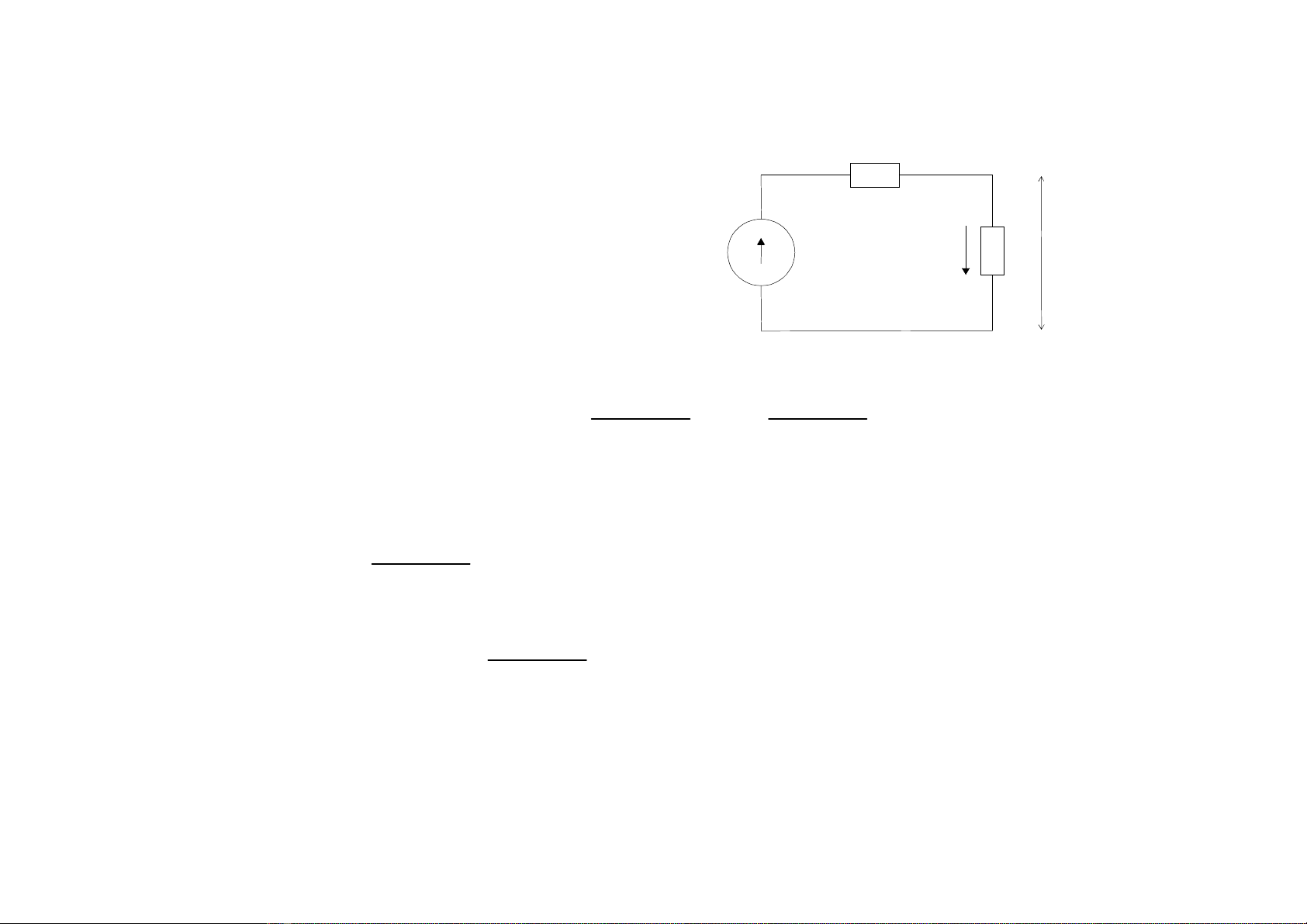
Láúyphæångtrçnh(2) nhánvåïiZ
1coï: ut-u
f= Ik.Z1 (3)
Láúy(1) + (3) : 2 ut= uk+ Ik.Z1 (4)
Biãøuthæïcnaìytæångâæångvåïisåâäöthaythãú
gäömnguäönâiãûnaïpbàòng2 láönsoïngtåïiu
o
=2ut
cungcáúpcho2 täøngtråíZ
1
,Z2màõcnäúitiãúpnhau
(hçnhbãn). Âoïchênhlaìsåâäöthaythãútheoqui
tàõcPeterson, duìngâãøxaïcâënhsoïngaïpvaìdoìng
khuïcxaûkhimäitræåìngtruyãönsoïngthayâäøi.
Z1
Ik
M
utZ2uk
Tæìsåâäönaìytaxaïcâënhâæåüccaïcthaìnhpháönsoïngnhæsau:
-Thaìnhpháönsoïngkhuïcxaû :
-Thaìnhpháönsoïngphaínxaû :
tt
t
kuu
ZZ
Z
Z
ZZ
u
u..
2
.
2
21
2
2
21
α=
+
=
+
=
tttkf uuuuu .).1( βα =−=−=
Trongâoï: -Hãûsäúkhuïcxaû
-Hãûsäúphaínxaû
21
2
2
ZZ
Z
+
=α
21
12
)1( ZZ
ZZ
+
−
=−= αβ
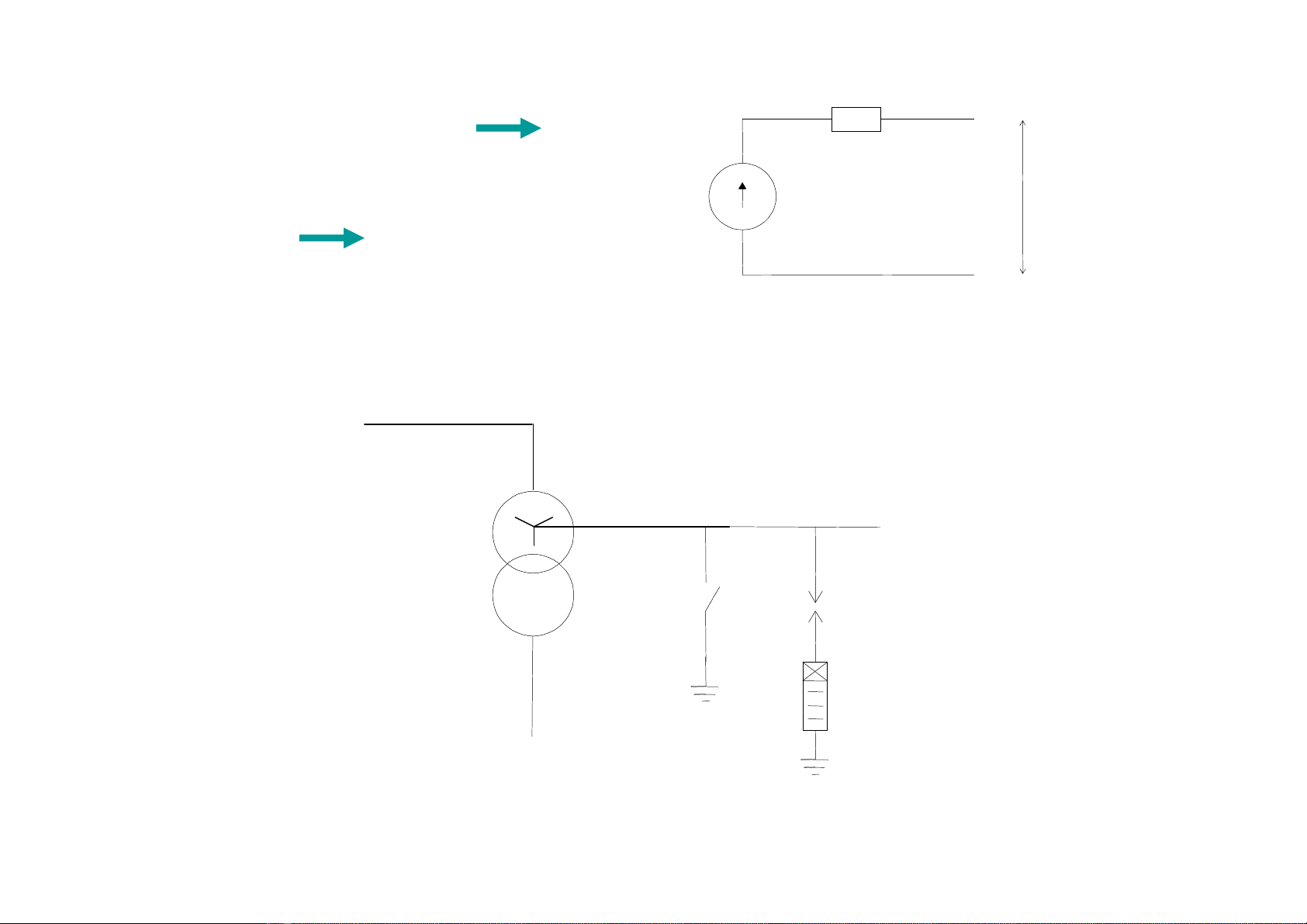
1) Xeïtcaïctræåìnggiåïihaûn:
2
=
α
=∝
2
Z* Træåìnghåüp1:
Z1
2ut
2utuk
1)1(
=
−
=
α
β
tf uu =
Hiãûntæåüngnaìygoüilaìhiãûntæåüngphaínxaûdæångaïptoaìnpháön
Træåìnghåüpnaìygàûpåíâáu?