13
ø
Trong ñoù: δ: Chieàu roäng khe hôû khoâng khí
hg: Chieàu cao cuûa goâng stator . hraêng: Chieàu cao raêng phaàn öùng.
hö: Chieàu cao cuûa löng phaàn öùng . hc: Chieàu cao cuûa cöïc töø .
Lg: Chieàu daøi trung bình ñöôøng söùc töø cuûa goâng töø .
Lö: Chieàu daøi trung bình ñöôøng söùc töø cuûa löng phaàn öùng .
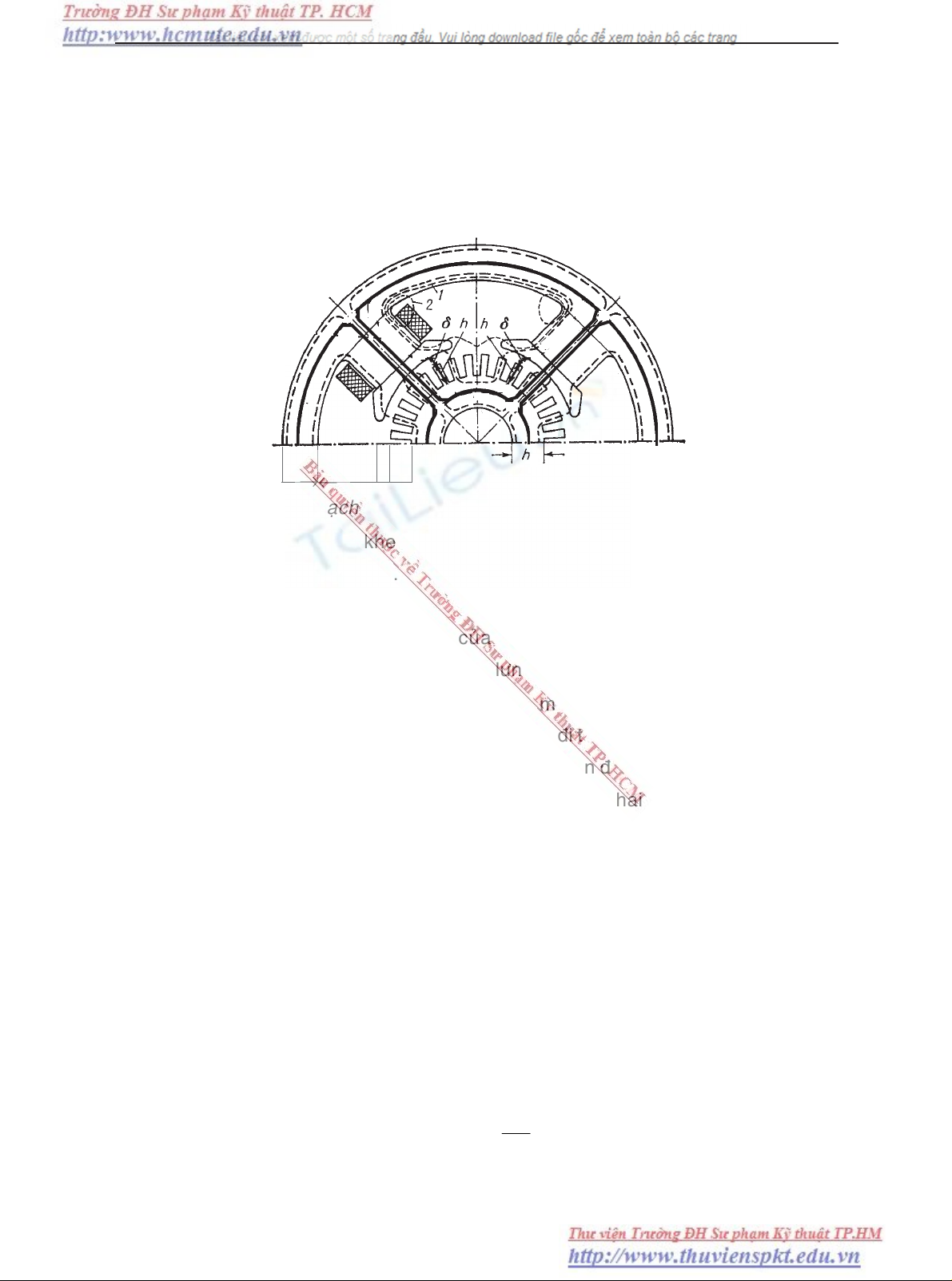
Treân hình 2-1 veõ sô löôïc moät phaàn cuûa maùy ñieän moät chieàu 4 cöïc vaø veõ
hình töø thoâng do caùc cöïc chính gaây neân. Töø thoâng ñi töø cöïc N qua khe hôû vaø phaàn
öùng roài trôû veà 2 cöïc S naèm keà beân. Do maùy hoaøn toaøn ñoái xöùng, neân töø thoâng do
moãi cöïc taïo neân bò chia ñoâi vôùi ñöôøng truïc cöïc thaønh hai phaàn taïo thaønh hai
maïch voøng töø gioáng nhau, ñaët ñoái xöùng caû veà hai phía ñoái vôùi ñöôøng truïc cöïc ñaõ
cho. Soá maïch voøng baèng soá cöïc cuûa maùy, nhöng khi tính söùc töø ñoäng chæ caàn xeùt
moät trong caùc maïch voøng ñoù. Phaàn töø thoâng ñi vaøo phaàn öùng goïi laø töø thoâng chính
hay töø thoâng khe hôû Φ0. Töø thoâng naøy caûm öùng neân s.ñ.ñ trong daây quaán khi phaàn
öùng quay vaø taùc duïng vôùi doøng ñieän trong daây quaán ñeå sinh ra moâmen.
Moät phaàn töø thoâng khoâng ñi qua phaàn öùng goïi laø töø thoâng taûn Φσ. Noù khoâng
caûm öùng neân söùc ñieän ñoäng trong phaàn öùng nhöng noù vaãn toàn taïi laøm cho ñoä baõo
hoaø töø trong cöïc töø vaø goâng töø taêng.
Neáu Φc laø toaøn boä töø thoâng do cöïc töø gaây neân thì:
σt laø heä soá taûn töø cuûa cöïc töø chính. σt = 1,15 - 1,28.
Söùc töø ñoäng F0 caàn thieát ñeå taïo ra töø thoâng chính laø söùc töø ñoäng chính.
ΦΦΦΦ Φ
ΦΦ
ct
=+= +
⎛
⎝
⎜⎞
⎠
⎟=
00
0
0
1
σ
σσ.(2-1)
Hình 2-1. Maïch töø cuûa maùy ñieän moät chieàu khi khoâng taûi
Chöông II
MAÏCH TÖØ CUÛA MAÙY ÑIEÄN MOÄT CHIEÀU KHI KHOÂNG TAÛI.
§ 2.1 Ñaïi cöông
Chöông naøy nhaèm trình baøy caùc phöông phaùp xaùc ñònh söùc töø ñoäng caàn
thieát cuûa cöïc töø chính F0 ñeå taïo ra töø thoâng chính Φ0 trong khe hôû khoâng khí giöõa
stator vaø rotor khi khoâng taûi.
→→→
→→→
r
r
ö
hraêng
hghCδ
→→
→→
→
→→
→→
→
→→
→→
→
→→
→→
→
→→
→→
→
→→
→→
→
→→
→→
→
→→
→→
→
14
ø
Theo ñònh luaät toaøn doøng ñieän:
∫∑
=
=== n
n
IWFHiLiHdl
1
Trong ñoù:
L
i
: Chieàu daøi trung bình cuûa ñöôøng söùc töø treân ñoaïn thöù i.
H
i
: Cöôøng ñoä töø tröôøng treân ñoaïn thöù i.
W: Soá voøng daây cuûa moät ñoâi cöïc töø.
I: Cöôøng ñoä doøng ñieän chaïy qua daây quaán kích töø.
Ñöôøng cong töø kheùp kín laø söï noái tieáp cuûa caùc ñoaïn ñöôøng söùc töø, caùc ñoaïn naøy ñi
qua caùc phaàn maïch töø coù ñoä töø thaåm khaùc nhau, trong maùy ñieän moät chieàu goàm 5
ñoaïn: Khe hôû khoâng khí, raêng phaàn öùng, phaàn öùng, cöïc töø vaø goâng töø. Caùc ñoaïn
naøy ñöôïc kyù hieäu töông öùng baèng caùc chæ soá: δ
,
raêng, ö, c vaø g.
Ta coù: F
0
= 2H
δ
δ + 2H
raêng
h
raêng
+ H
ö
L
ö
+ 2H
c
h
c
+ H
g
L
g.
F
0
= F
δ
+ F
raêng
+ F
ö
+F
c
+F
g.
(2-3)
Do ñoù ñeå tính söùc töø ñoäng toång cuûa moät ñoâi cöïc töø F
o
ta phaûi tính söùc töø ñoäng
treân töøng phaàn maïch töø treân.
Töø phöông trình (2-3) ta thaáy muoán tính S.t.ñ ñoái vôùi moãi ñoaïn trong 5 ñoaïn caàn
phaûi tìm cöôøng ñoä töø tröôøng H töông öùng vaø nhaân noù vôùi chieàu daøi maïch töø ñoù.
Neáu ñaõ bieát töø thoâng Φ vaø kích thöôùc hình hoïc cuûa caùc ñoaïn thì coù theå tính B töø
caûm cuûa caùc ñoaïn maïch töø theo coâng thöùc . Trong ñoù S laø tieát dieän cuûa
caùc phaàn maïch töø.
Trong khoâng khí µ
o
= 4π10
-7
H/m. Nhöng trong saét töø µ = C
te
neân ta khoâng
tröïc tieáp tính H ñöôïc maø tìm H theo ñöôøng ñaëc tính töø hoùa cuûa vaät lieäu B = f(H) khi
bieát B.
Sau khi phaân ñoaïn tính ñöôïc s.t.ñ treân caùc ñoaïn coù theå tìm ñöôïc s.t.ñ toång
döôùi moãi ñoâi cöïc töø F
0
.
(2-2)
§ 2.2 Tính söùc töø ñoäng khe hôû F
δ
Khe hôû laø trôû löïc chính ñoái vôùi töø thoâng. do ñoù S.t.ñ khe hôû F
δ
thöôøng chieám
khoâng döôùi 60% s.t.ñ chính F
o
. Ñeå tính F
δ
ta tieán haønh :
- Tröôùc tieân ta giaû söû beà maët phaàn öùng phaúng khoâng coù raõnh vaø raêng, khe hôû ôû giöõa
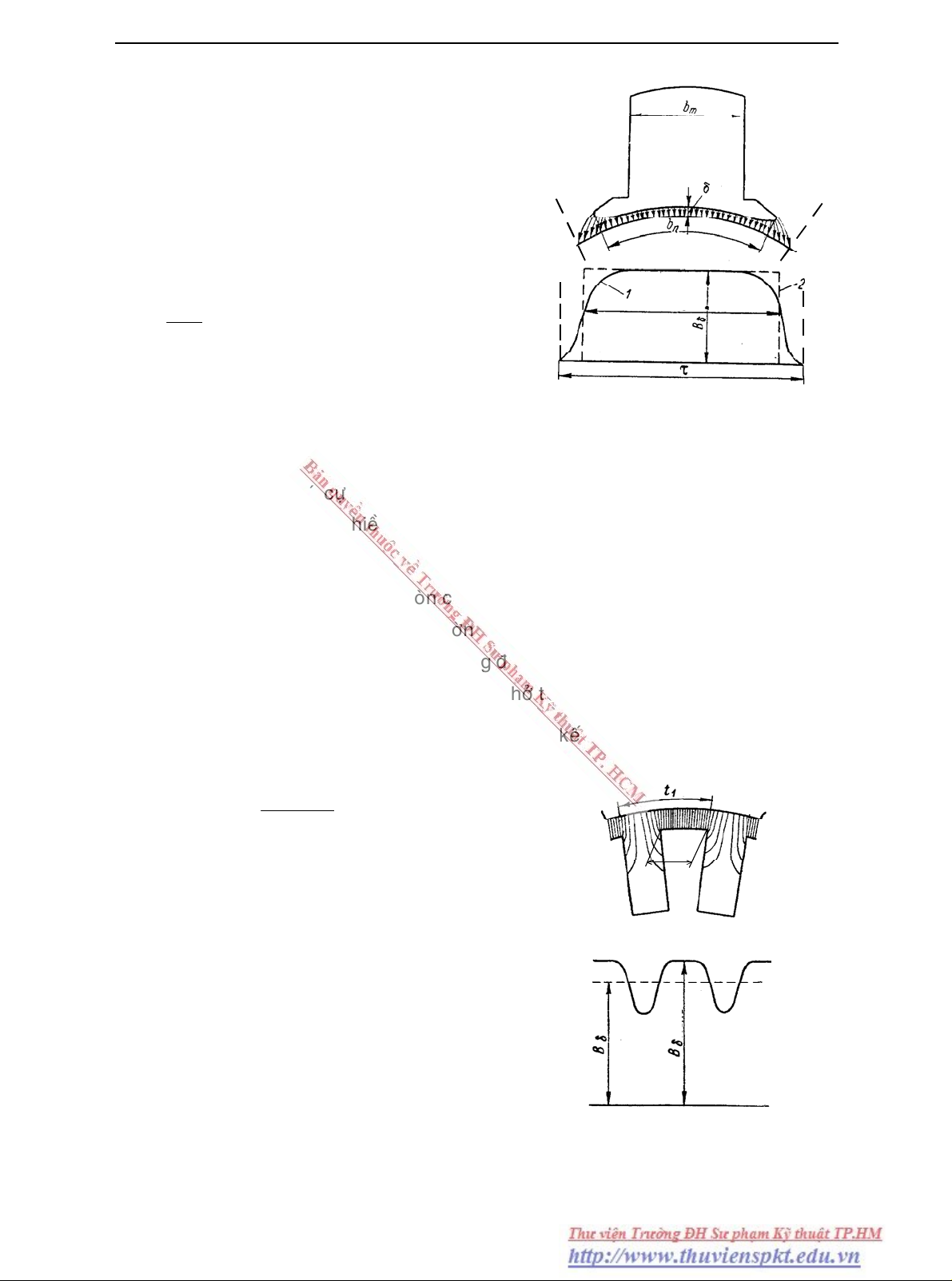
cöïc töø laø beù nhaát thì söï phaân boá töø caûm döôùi cöïc töø coù daïng nhö hình 2-2. Hình
daùng cuûa noù phuï thuoäc vaøo beà roäng cuûa maët cöïc töø vaø chieàu daøi cuûa khe hôû. ÔÛ giöõa
töø caûm B lôùn nhaát, ôû hai meùp cöïc thì nhoû ñi nhieàu vaø baèng khoâng ôû ñöôøng trung
S
BΦ
=
15
ø
tính hình hoïc (TTHH). Ñeå deã tính F
δ
chuùng
ta ñôn giaûn hoùa ñöôøng phaân boá töø caûm theo
phöông phaùp ñaúng trò, nghóa laø coi ñöôøng
phaân töø caûm laø hình chöõ nhaät coù chieàu cao
max
BB δδ =, chieàu ñaùy laø τα= δ.b' sao cho
dieän tích hình chöõ nhaät baèng dieän tích ñöôøng
cong. Trong ñoù:
laø böôùc cöïc: khoaûng caùch giöõa 2
cöïc töø
D
ö
:ñöôøng kính phaàn öùng ; p : soá ñoâi cöïc töø
δ
α: heä soá tính toaùn cung cöïc töø; b
/
chieàu daøi
tính toaùn cung cöïc töø. Trong caùc maùy ñieän
moät chieàu khoâng coù cöïc töø phuï δ
α= 0,7 -
0,8. Caùc maùy ñieän moät chieàu coù cöïc töø phuï
δ
α= 0,62 - 0,72.
Hình 2-2. Ñöôøng phaân boá thöïc teá (1) vaø ñaúng
trò (2) cuûa töø tröôøng trong khe hôû khoâng khí
treân tieát dieän ngang cuûa phaàn öùng nhaün
- Treân thöïc teá maët cöïc töø coøn coù raêng vaø raõnh, neân töø tröôøng trong khe hôû
phaân boá caøng khoâng ñeàu, treân raêng ñöôøng söùc töø daøy, coøn ôû raõnh thì thöa thôùt hôn.
Kích thöôùc cuûa raêng vaø raõnh coù aûnh höôûng ñeán ñöôøng ñi cuûa ñöôøng söùc töø. Vì vaäy
khi tính toaùn Fδ caàn phaûi duøng chieàu daøi khe hôû tính toaùn δ’: δ=δ δ.' k. Trong ñoù:
kδ: heä soá khe hôû, ñöôïc cho trong caùc soå tay thieát keá maùy ñieän. Ñoái vôùi raõnh chöõ
nhaät ta coù theå duøng coâng thöùc:
kt
br
δ
δ
δ
=+
+
1
1
10
10 (2-4)
t
1
: böôùc raêng theo chu vi phaàn öùng.
b
r1
: chieàu roäng cuûa ñænh raêng.
- Ñoái vôùi maùy ñieän coâng suaát lôùn, theo
chieàu daøi loõi saét coù caùc raõnh thoâng gioù höôùng
kính neân töø caûm doïc truïc cuõng phaân boá khoâng
ñeàu.
Thay ñöôøng cong phaân boá töø caûm thöïc teá baèng
hình chöõ nhaät coù chieàu roäng Bδ = Bδ
max
vaø chieàu
daøi lδ = 0,5(l
C
+ l).
Hình 2-3. Töø caûm trong khe hôû khoâng
khí khi phaàn öùng coù raêng vaø raõnh
′=bατ
δ
TTHH TTHH
TTHH
TTHH
b
r1
Max
p2
D
ö
π
=τ
16
ø
lδ
lC
lö
bg
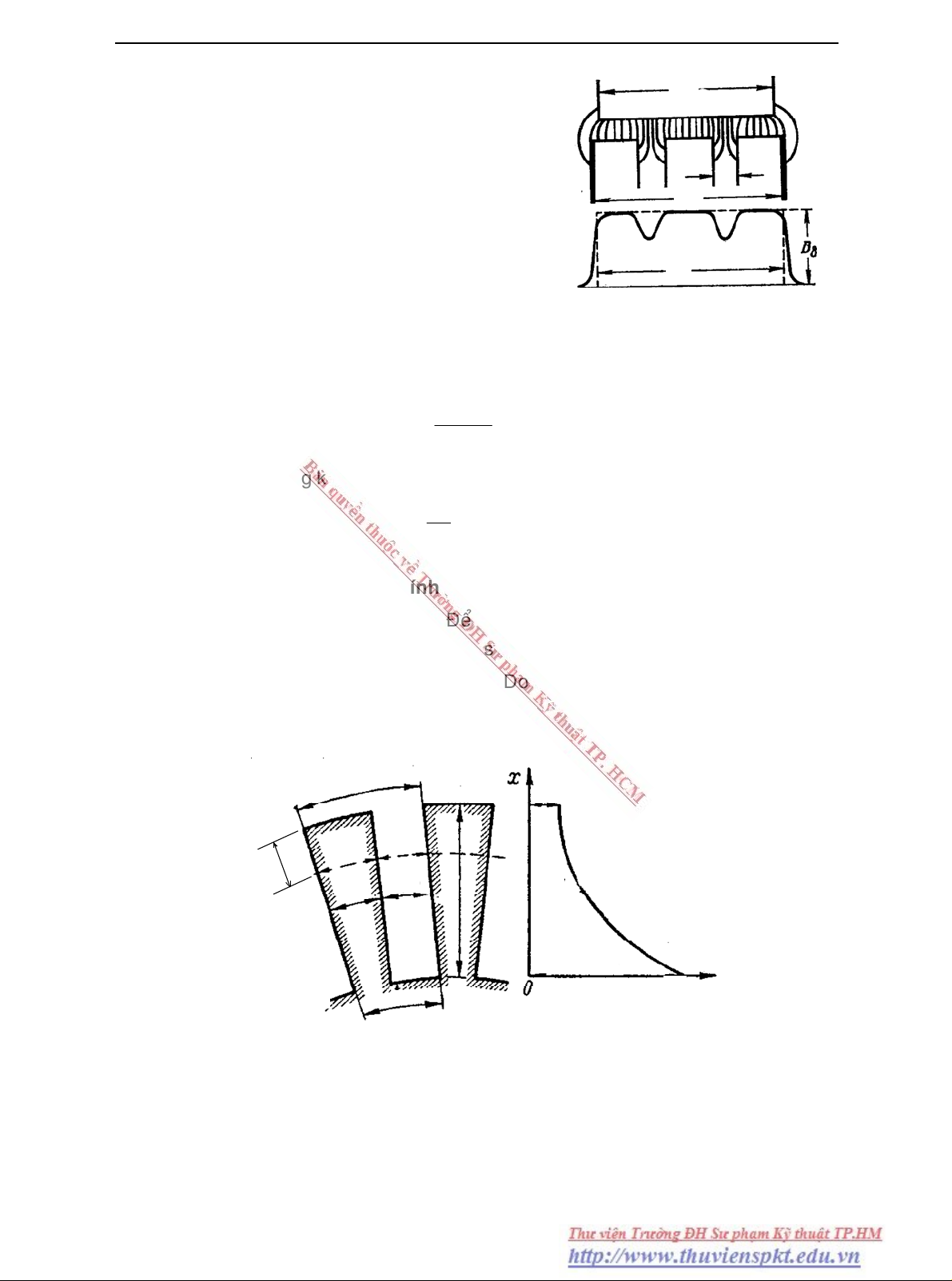
Hình 2-4. Hình thaät vaø hình tính ñoåi
cuûa töø tröôøng trong khe hôû treân tieát
dieän doïc cuûa phaàn öùng
Trong ñoù :
lδ laø chieàu daøi tính toaùn cuûa phaàn öùng .
lC laø chieàu daøi cuûa cöïc töø theo höôùng doïc truïc.
l = lö – ng.bg chieàu daøi thöïc cuûa loõi saét
phaàn öùng khoâng tính ñeán raõnh thoâng gioù.
lö chieàu daøi thöïc cuûa loõi saét.
ng , bg : soá raõnh vaø chieàu roäng raõnh thoâng gioù.
Nhö vaäy vôùi 1 töø thoâng chính Φ0 naøo ñoù thì töø
caûm laø :
Bl
δ
ο
δδ
ατ
=Φ
..
Vaø söùc töø ñoäng trong khe hôû khoâng khí laø:
FBk
δ
ο
δδ
µδ= 2.. (A/ñoâi cöïc) (2-5)
§ 2.3 Tính söùc töø ñoäng raêng
Raõnh phaàn öùng coù nhieàu kieåu. Ñeå ñôn giaûn ta laáy moät kieåu raõnh laø hình chöõ
nhaät (raêng seõ laø hình thang).Töø thoâng Φ0sau khi ñi qua khe hôû khoâng khí thì phaân
laøm 2 maïch song song ñi vaøo raêng vaø raõnh. Do töø daãn cuûa theùp lôùn hôn khoâng khí
neân ñaïi boä phaän Φ0 ñi vaøo raêng.
Hình 2-5. Söùc töø ñoäng raêng
braêng x
t1
braõnhx
braêngtb
braêng2
t2
Töø thoâng trong khe hôû ñoái vôùi moät böôùc raêng (chæ caàn tính S.t.ñ cuûa caùc raêng ñoái
vôùi 1 böôùc raêng laø ñuû vì taát caû caùc raêng ñeàu daãn töø thoâng song song vôùi nhau vaø
taát caû chuùng ñeàu naèm trong nhöõng ñieàu kieän töø tröôøng gioáng nhau, treân chieàu daøi
cuûa cung cöïc b’) baèng:
Β/
raêng x
x
17
ø
Φt = Bδ.t1.lδ
Laáy moät tieát dieän ñoàng taâm vôùi maët phaàn öùng caùch ñænh raêng moät khoaûng x
ñeå xeùt, thì töø thoâng Φt ñi qua tieát dieän ñoù goàm 2 phaàn:
- Φraêng x ñi qua raêng.
- Φraõnhx ñi qua raõnh.
Ta coù:
Φt =Φraêng x + Φraõnh x (2-7)
Chia hai veá cuûa (2-7) cho tieát dieän maët caét cuûa raêng, ta coù:
(2-8)
:Goïi laø töø caûm tính toaùn cuûa raêng. YÙ nghóa cuûa noù laø coi nhö toaøn boä
töø thoâng ñeàu ñi qua raêng. Khi B/raêng x > 1,8T thì do maïch töø treân raêng töông ñoái baõo
hoøa neân töø thoâng trong raõnh khoâng theå boû qua ñöôïc, phaûi phaân bieät B/raêng x vaø Braêngx
raêngx
raêngx
raêngx
SΒ=
Φ: töø caûm thöïc teá trong raêng.
Coù theå vieát:
(2-6)
..
.1-
klb
lt
=
S
S-S
=
S
S
=k
craêngx
x
x raêng
x raêngtx
raêngx
raõnhx
raêngx δ(2-10)
Trong ñoù:
Stx: Tieát dieän böôùc raêng ôû ñoä cao x.
tx: Böôùc raêng ôû ñoä cao x.
l: Chieàu daøi loõi theùp thuaàn öùng (khoâng keå raõnh thoâng gioù höôùng kín).
kc: Heä soá eùp chaët loõi theùp (tyû soá giöõa chieàu daøi thuaàn theùp cuûa loõi theùp vôùi
chieàu daøi thöïc cuûa loõi theùp).
Trong ñoù: Sraõnhx: Tieát dieän ngang cuûa raõnh.
Braõnhx: töø caûm tieát dieän trong raõnh ñaõ cho.
Hraõnhx: cöôøng ñoä töø tröôøng trong tieát dieän raõnh ñaõ cho.
kraêngx: heä soá raêng.
raêngx
raõnhx
raõnhx
raõnhx
raêngx
raõnhx S
S
SS .
Φ
=
Φ
raêngxraõnhx0raêngxraõnhx
kH=kB= ... µ(2-9)
raêngx
raõnhx
raêngx
raêngx
raêngx
tSSS
Φ
+
Φ
=
Φ
/
raêngx
raêngx
tB
S=
Φ