1
Giáo trình thuỷ khí
Chuyển động thế phẳng
2
Chương 8 chuyển động thế phẳng
Mục đích: Nghiên cứu một số đặc trưng động lực học
của chuyển động thế phẳng của chất lỏng lý tưởng
Phương pháp: Sử dụng lý thuyết hàm biến phức
8.1- ứng dụng hàm biến phức
I. Thế phức:
Dòng chất lỏng lý tưởng chuyển động có thế khi thoả
mãn điều kiện:
0urot
Khi đó ta đưa vào hàm thế vận tốc , trong đó các
thành phần vận tốc được xác định:
i
ui
(i=x,y,z) (1)
Vectơ vận tốc: gradu
Ta giả thiết ;
dt
d
; 2
2
dt
d là liên tục theo toạ độ
Ta nhận thấy bất kỳ hàm + C nào cũng thoả mãn (1) :
thế của trường vận tốc chính xác đến hằng số.
Đối với chuyển động thế dừng: =(x,y,z); khi
=(x,y,z)=const ta được phương trình mặt đẳng thế
(mặt có thế bằng nhau)
Lý thuyết giải tích vectơ cho thấy: vectơ grad vuông
góc với mặt =const do đó trên mặt đẳng thế vecơ vận
tốc tại mọi điểm sẽ vuông góc với nó.
Xét chuyển động thế, phẳng, dừng, khi đó chất lỏng di
chuyển trong mặt phẳng xOy, thế vận tốc được xác
định như sau:
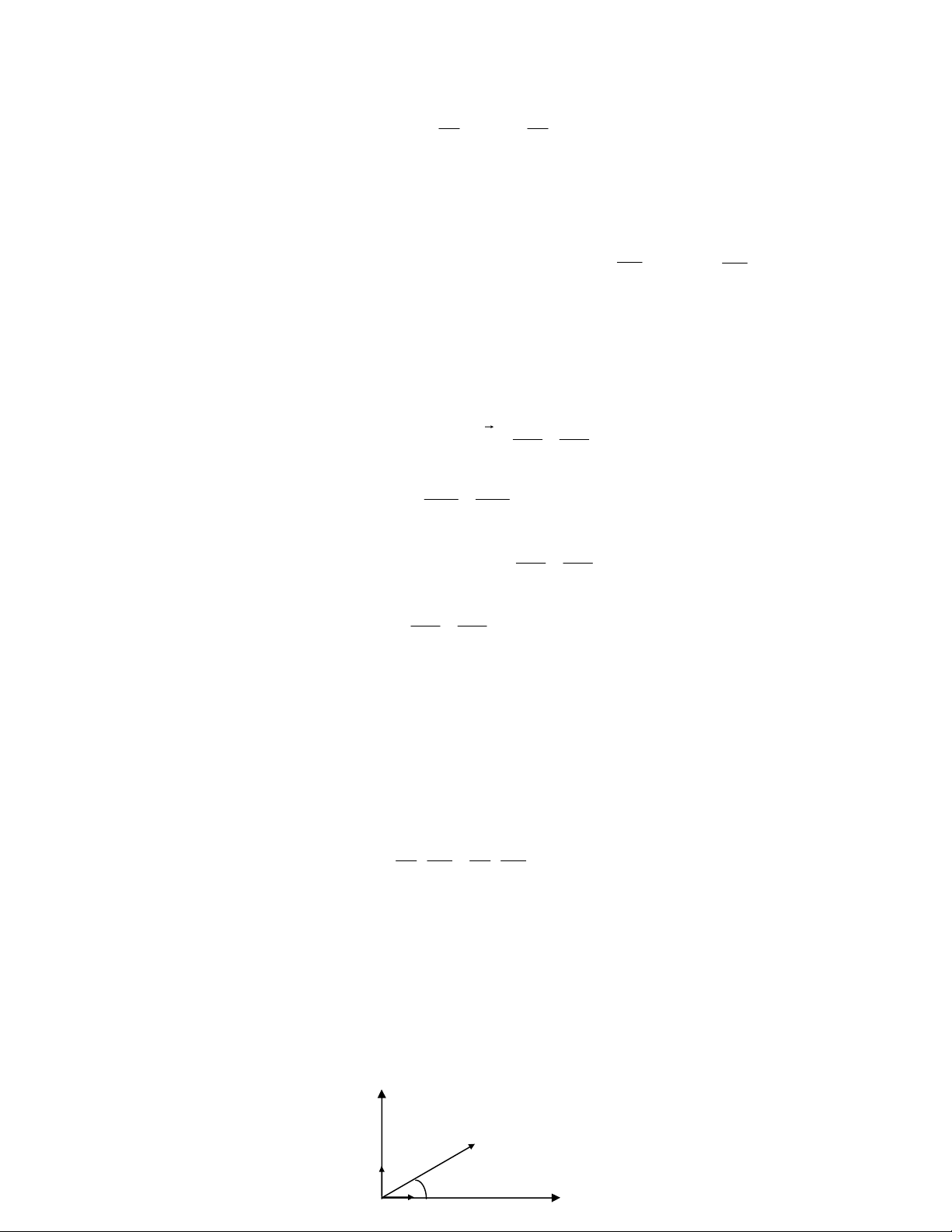
3
x
ux
; y
uy
Phương trình các đường đẳng thế trong mặt phẳng xOy
sẽ là: (x,y) = C
Gọi hàm (x,y) thoả mãn điều kiện: y
ux
;
x
uy
Biểu thức (x,y) = C là phương trình đường dòng
Hàm thế và hàm dòng thoả mãn phương trình
Laplace; bởi vì:
Từ điều kiện không xoáy: 0
x
u
x
u
urot x
y
x
ta có 0
yx 2
2
2
2
Từ phương trình liên tục: 0
y
u
x
uy
x
ta có 0
yx 2
2
2
2
Như vậy hàm thế và hàm dòng là các hàm điều hoà
(Laplace=0)
Ta nhận thấy hàm thế và hàm dòng thoả mãn điều kiện
Cauchy-Riemann (điều kiện trực giao giữa đường dòng
và đường đẳng thế)
0
yyxx
Trong lý thuyết hàm biến phức, nếu và là các hàm
điều hoà và thoả mãn điều kiện Cauchy- Riemann thì
hàm phức (x,y) + i(x,y) là hàm của 1 biến số phức z
với z= x+iy=r(cos+isin)=e.exp(i)
Như vậy tồn tại hàm phức W(z)= (x,y) + i(x,y) và
còn gọi là thế phức.
x
i
4
Hình 1
II. Vận tốc phức
Lý thuyết hàm biến phức cho:
)iy(d
dW
dx
dW
dz
dW
nghĩa là đạo hàm
dz
dW và đạo hàm theo 2 phương của trục
thực và trục ảo bằng nhau, ta có thể chứng minh:
uiuu
yy
i
dy
dW
i
iyd
dW
uiuu
x
i
xdx
dW
yx
yx
u=ux+iuy gọi là vận tốc phức; u= ux+iuy gọi là vận tốc
liên hợp; mặt phẳng (ux,uy) gọi là mặt phẳng vận tốc.
Kết luận: Để khảo sát chuyển động thế phẳng của chất
lỏng lý tưởng ta áp dụng lý thuyết hàm biến phức, mỗi
thế phức tương ứng với 1 chuyển động nào đấy của chất
lỏng; ngược lại, một chuyển động thế sẽ được biểu
diễn bằng một thế phức nào đấy. Từ đấy ta có 2 loại
bài toán:
- Xác định chuyển động (trường vận tốc) khi cho biết
thế phức.
- Xác định thế phức khi cho biết đường biên của vật
bị bao quanh và vận tốc ở vô cùng.
8.2 – Một số chuyển động đơn giản:
5
I. Chuyển động phẳng:
Thế phức
iyxaazzW trong đó a là hằng số.
Ta có 2 cas:
a) a là số thực a1
iiyxazazW 11
Do đó = a1x và = a1y
Đường đẳng thế: = a1x = Const là họ các đường thẳng
song song với trục y.
Các đường dòng: = a1y = Const là họ các đường thẳng
song song với trục y.
Các thành phần vận tốc: 1x a
yx
u
0
xy
uy
Vậy ta có chuyển động thẳng theo phương x (hình2a)
b) a là số ảo: a = ia1 (a1 là số thực); tương tự
như trên, ta tìm được:
Đường đẳng thế: = - a1y = Const là họ các đường
thẳng song song với trục x.
Hình 2a
=cons
t
y
x
=con
u
x
=cons
y
x
=con
Hình 2b