MATLAB trong ñieàu khieån töï ñoäng Trang 255
KHAÛO SAÙT SÖÏ OÅN ÑÒNH CUÛA HEÄ THOÁNG
LYÙ THUYEÁT:
• Heä thoáng oån ñònh ôû traïng thaùi hôû, seõ oån ñònh ôû traïng thaùi kín neáu bieåu ñoà Nyquist
khoâng bao ñieåm (-1+i0) treân maët phaúng phöùc.
• Heä thoáng khoâng oån ñònh ôû traïng thaùi hôû, seõ oån ñònh ôû traïng thaùi kín neáu bieåu ñoà
Nyquist bao ñieåm (-1+i0)p laàn ngöôïc chieàu kim ñoàng hoà (p laø soá cöïc GH naèm ôû phaûi maët
phaúng phöùc).
Töø daáu nhaéc cuûa cöûa soå MATLAB, ta nhaäp:
» num = [nhaäp caùc heä soá cuûa töû soá theo chieàu giaûm daàn cuûa soá muõ].
» den = [nhaäp caùc heä soá cuûa maåu soá theo chieàu giaûm daàn cuûa soá muõ].
» nyquist(num,den)
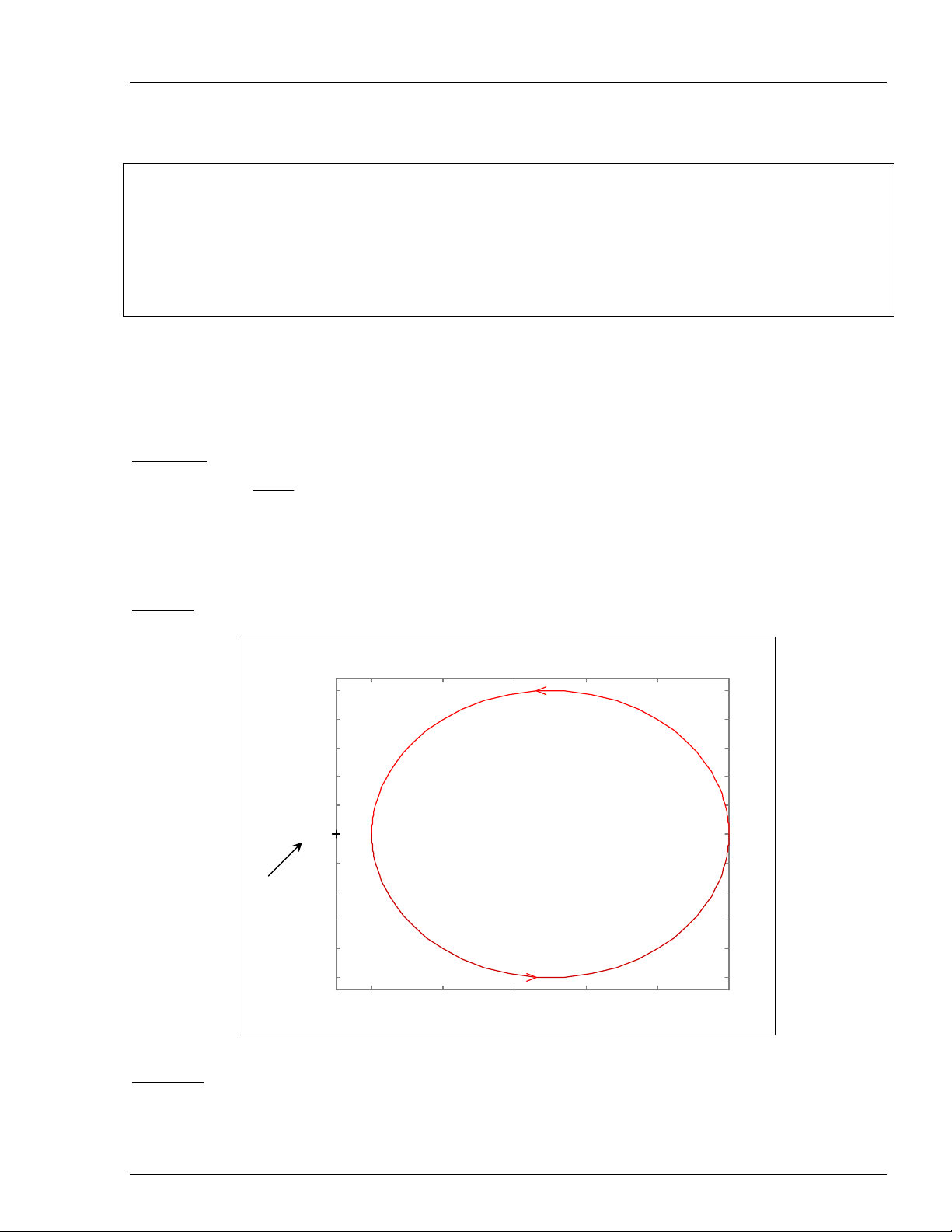
Baøi taäp 1:
GH(s) = st1
k
− (vôùi k =10, t =1)
» num = 10;
» den = [-1 1];
» nyquist(num,den)
Keát quaû:
Real Ax is
Imaginary Axis
Nyqui st Di agr am s
0246810
-5
-4
-3
-2
-1
0
1
2
3
4
5
(A)
Nhaän xeùt: haøm truyeàn voøng hôû coù 1 cöïc naèm beân phaûi maët phaúng phöùc. Bieåu ñoà Nyquist khoâng
bao ñieåm A (-1+j0).
MATLAB trong ñieàu khieån töï ñoäng Trang 256
Ñieåm –1 kyù hieäu (+) naèm treân truïc thöïc aâm (Real Axis), ñieåm 0 naèm treân truïc aûo
(Imaginary Axis).
Keát luaän: heä khoâng oån ñònh.
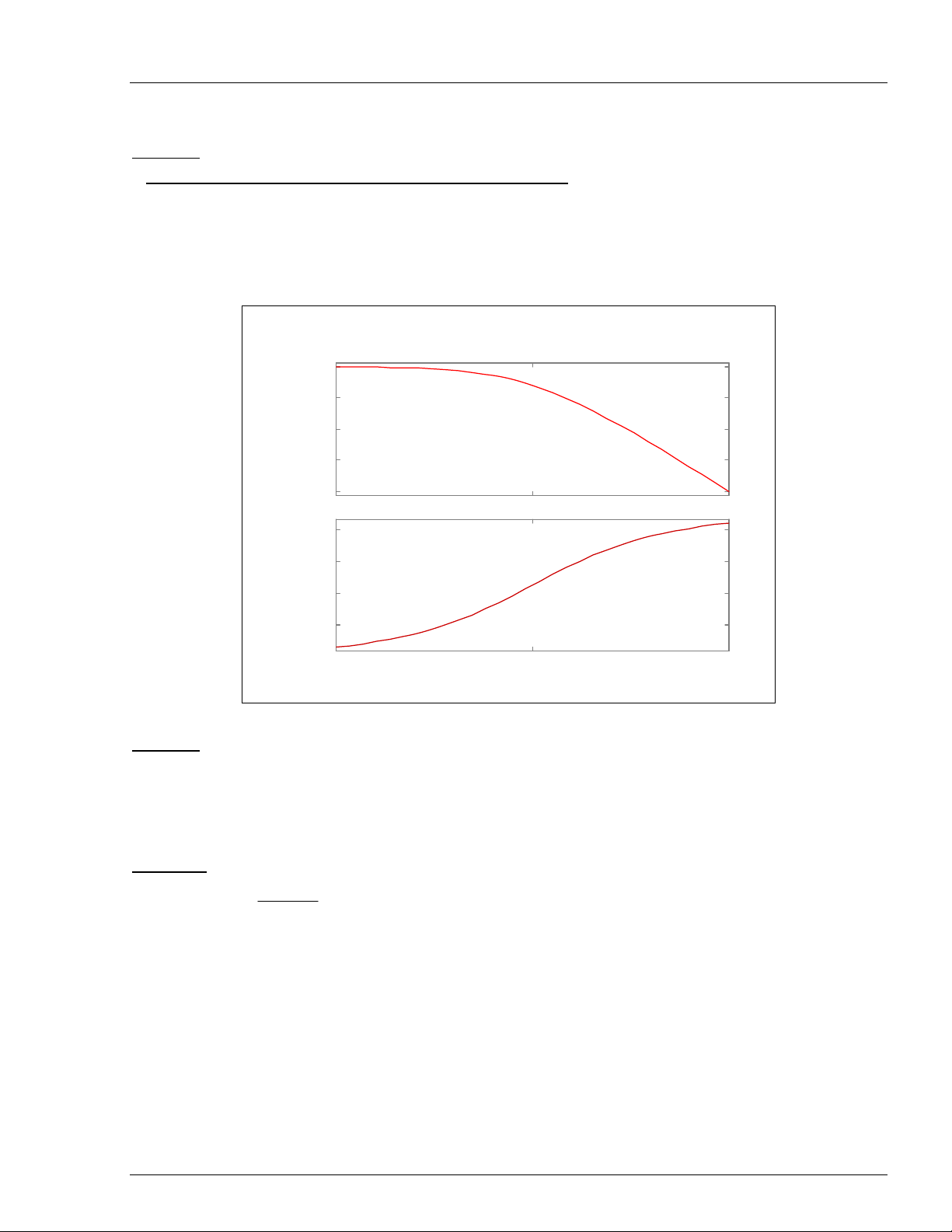
* Duøng leänh margin ñeå tìm bieân döï tröõ vaø pha döï tröõ.
Töø daáu nhaéc cuûa cöûa soå leänh MATLAB ta duøng leänh ‘margin’:
» num = 10;
» den = [-1 1];
» margin(num,den);
Frequency (rad/sec)
Phase (deg); Magnitude (dB)
Bode Diagrams
0
5
10
15
20
Gm = 0 dB, Pm = 0 (unstable closed loop)
10
0
20
40
60
80
Keát luaän:
Ñoä döï tröõ bieân (Gm = 0 dB).
Ñoä döï tröõ pha (Pm = 0°).
Warning: Closed loop is unstable (heä voøng kín khoâng oån ñònh).
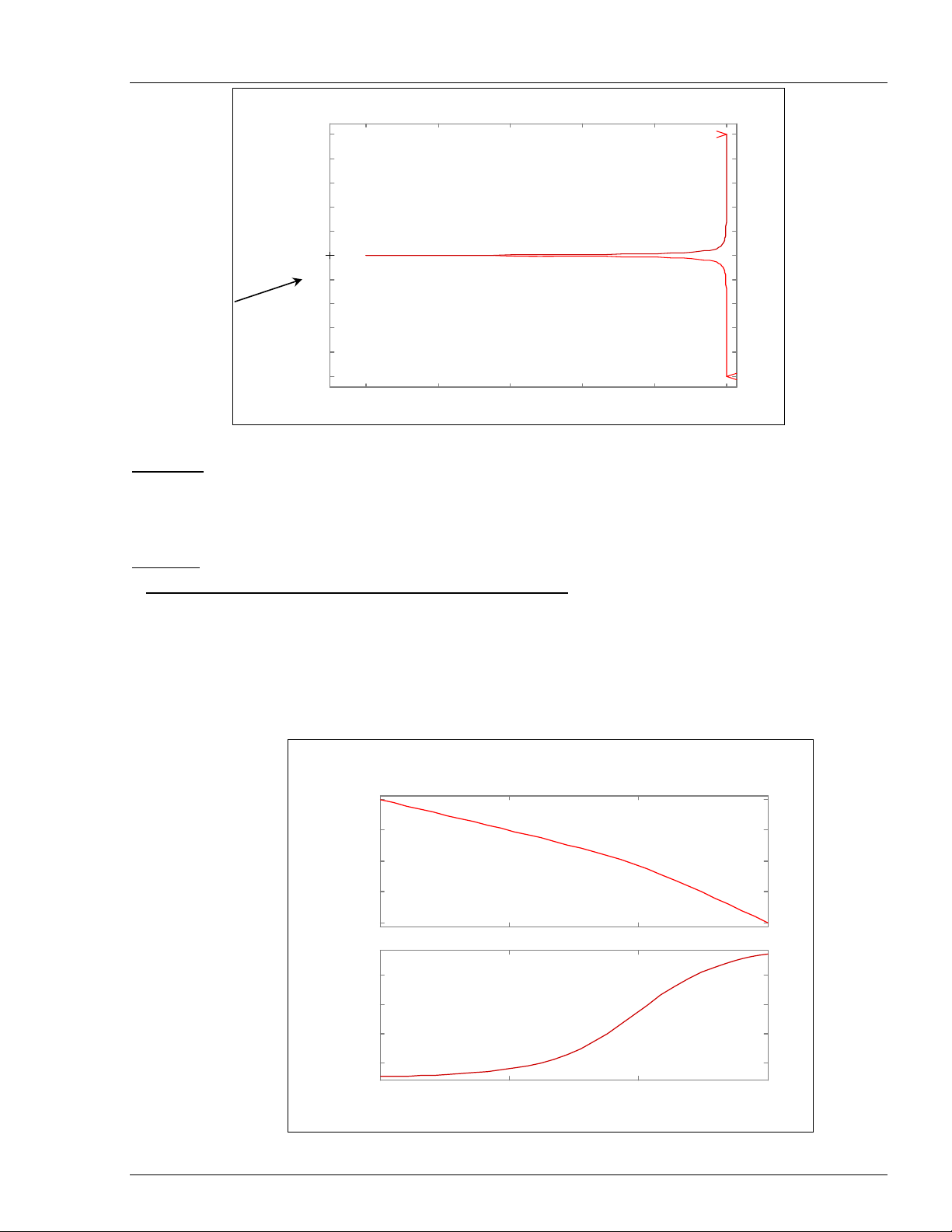
Baøi taäp 2:
GH(s) =
()
st1s
k
− (k = 10, t = 1)
» num = 10;
» den = [-1 1 0];
» nyquist(num,den)
MATLAB trong ñieàu khieån töï ñoäng Trang 257
Real Ax i s
inary Axis
Nyqui st Diagram s
Imag
0 2 4 6 8 10
-1000
-800
-600
-400
-200
0
200
400
600
800
1000
(A)
Nhaän xeùt: haøm truyeàn voøng hôû coù 1 cöïc naèm beân phaûi maët phaúng phöùc vaø 1 cöïc naèm taïi goác toïa
ñoä. Bieåu ñoà Nyquist khoâng bao ñieåm A (-1+j0).
Ñieåm –1 kyù hieäu (+) naèm treân truïc thöïc aâm (Real Axis) , ñieåm 0 naèm treân truïc aûo (Imaginary
Axis).
Keát luaän: heä khoâng oån ñònh.
* Duøng leänh margin ñeå tìm bieân döï tröõ vaø pha döï tröõ.
Töø daáu nhaéc cuûa cöûa soå leänh MATLAB ta duøng leänh ‘margin’:
» num = 10;
» den = [-1 1 0];
»margin(num,den)
Frequency (rad/sec)
Phase (deg); Magnitude (dB)
Bode Diagrams
-20
0
20
40
60
Gm = 0 dB, Pm = 0 (unstable closed loop)
10
-1
10
0
-80
-60
-40
-20
MATLAB trong ñieàu khieån töï ñoäng Trang 258
Keát luaän:
Ñoä döï tröõ bieân (Gm = 0 dB).
Ñoä döï tröõ pha (Pm = 0°).
Warning: Closed loop is unstable (heä voøng kín khoâng oån ñònh).
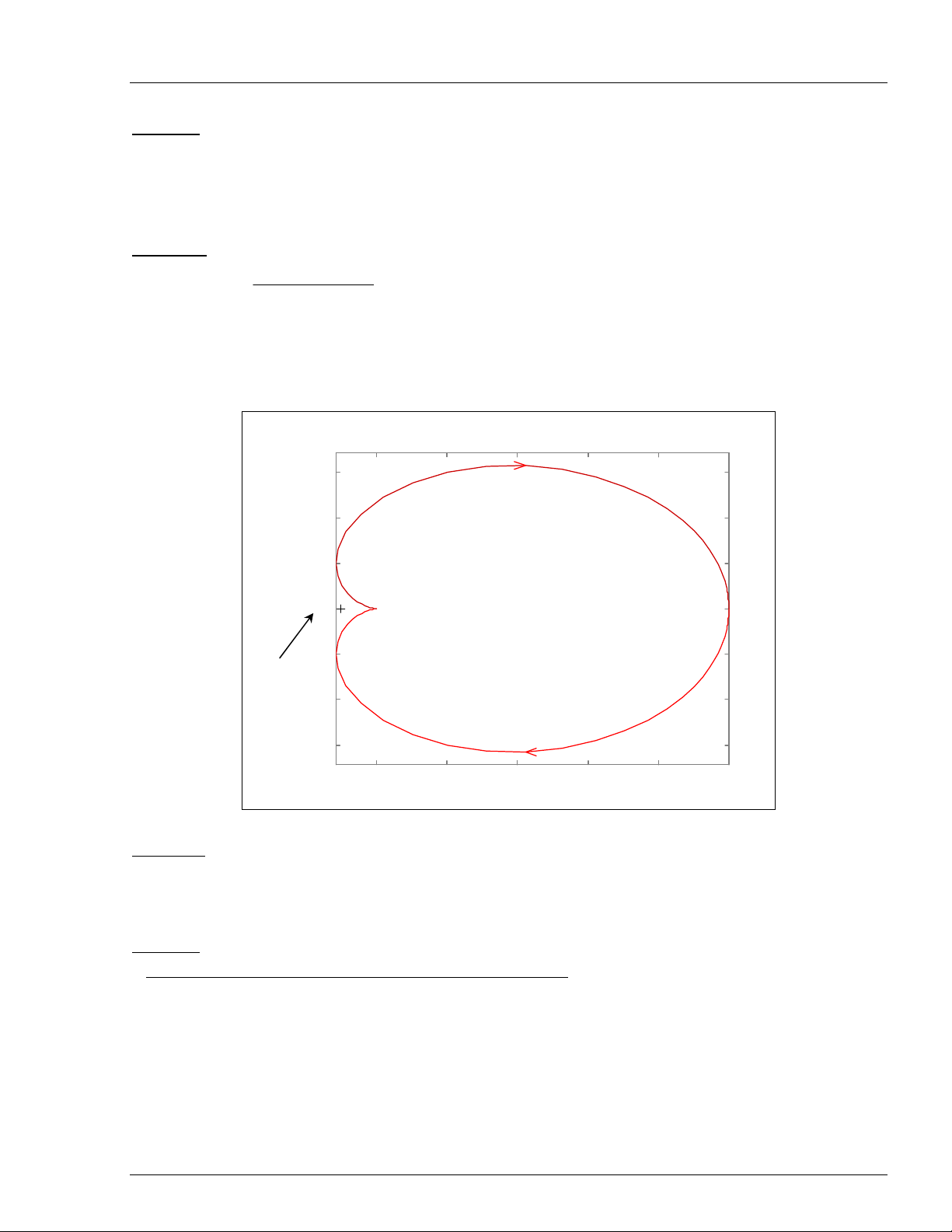
Baøi taäp 3:
GH(s) =
()()
1st1st
k
21 ++ (k =10, t1 = 1, t2 = 2)
» num = 10;
» den = [2 3 1];
» nyquist(num,den)
Real Ax is
ry Axis
Nyqui st Di agr am s
Imagina
0 2 4 6 8 10
-6
-4
-2
0
2
4
6
(A)
Nhaän xeùt: haøm truyeàn voøng hôû coù 2 cöïc naèm beân traùi maët phaúng phöùc. Bieåu ñoà Nyquist khoâng
bao ñieåm A (-1+j0).
Ñieåm –1 kyù hieäu (+) naèm treân truïc thöïc aâm (Real Axis) , ñieåm 0 naèm treân truïc aûo
(Imaginary Axis).
Keát luaän: heä thoáng oån ñònh.
* Duøng leänh margin ñeå tìm bieân döï tröõ vaø pha döï tröõ.
Töø daáu nhaéc cuûa cöûa soå MATLAB duøng leänh ‘margin’.
» num = 10;
» den = [2 3 1];
» margin(num,den)
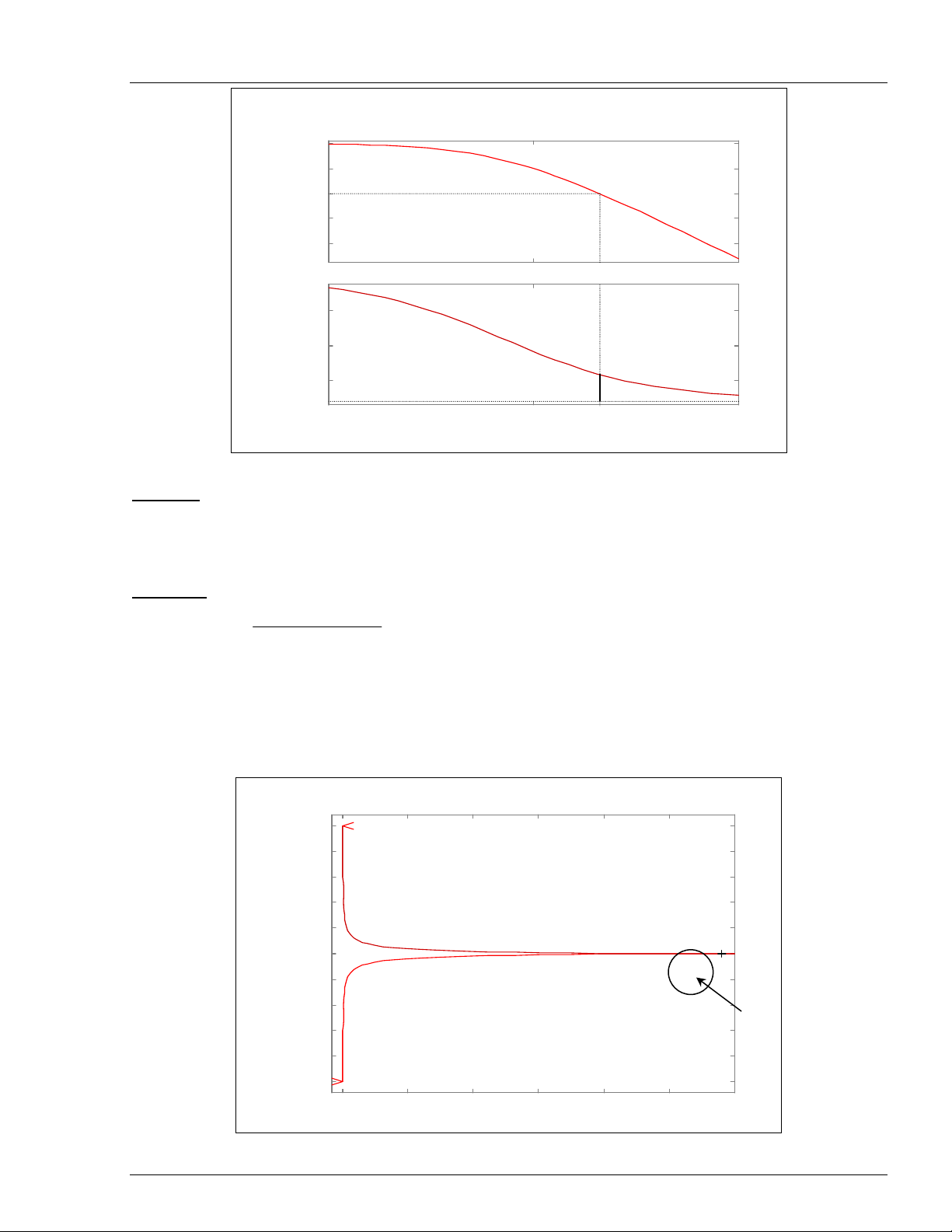
MATLAB trong ñieàu khieån töï ñoäng Trang 259
Frequency (rad/sec)
Phase (deg); Magnitude (dB)
Bode Diagrams
-20
-10
0
10
20
Gm = Inf, Pm=38.94 deg. (at 2.095 rad/sec)
10
0
-150
-100
-50
Keát luaän: heä thoáng oån ñònh.
Ñoä döï tröõ bieân (Gm = ∞).
Ñoä döï tröõ pha (Pm = 38.94°), taïi taàn soá caét bieân 2.095 rad/sec.
Baøi taäp 4:
GH(s) =
()()
1st1sts
k
21 ++ (k = 10 t1=1, t2 =2)
» num = 10;
» den = [2 3 1 0];
» nyquist(num,den)
Real Axis
Imaginary Axis
Nyqu i st Di agrams
-30 -25 -20 -15 -10 -5
-1000
-800
-600
-400
-200
0
200
400
600
800
1000
(A)