H C VI N CÔNG NGH B U CHÍNH VI N THÔNGỌ Ệ Ệ Ư Ễ C NG HOÀ XÃ H I CH NGHĨA VI T NAMỘ Ộ Ủ Ệ
H I ĐNG RA Đ THI MÔN H C, H C PH NỘ Ồ Ề Ọ Ọ Ầ Đc l p - T do – H nh phúcộ ậ ự ạ
NGÂN HÀNG Đ THI Ề
Môn: ĐI S Ạ Ố
Ban hành kèm theo Quy t đnh s : ………/ c a Giám đcế ị ố ủ ố
H c vi n Công ngh B u chính vi n thông ký ngày /12/2010ọ ệ ệ ư ễ
DÙNG CHO ĐÀO T O H ĐI H C CHÍNH QUY NGÀNH VI N THÔNG, K THU T ĐI N T , Ạ Ệ Ạ Ọ Ễ Ỹ Ậ Ệ Ử
CÔNG NGH THÔNG TIN Ệ
M I Đ 4 CÂUỖ Ề ( m i ph n ch n m t câu và có t ng đi m b ng 10)ỗ ầ ọ ộ ổ ể ằ
A. PH N 1 Ầ
Lo i 2 đi mạ ể
Câu A 1.2:
DCBA ,,,
là t p con c a ậ ủ
E
. Ch ng minh r ng:ứ ằ
a) N u ế
DCBA ,
thì
A C B D� � �
và
A C B D� � �
.
b) N u ế
BACABACA ,
thì
BC
.
Câu A 2.2: Đt ặ
{ }
1,2,3, 4,5,6,7,8A=
,
{ }
1,3,5,7,9B=
,
và
là các t p con c a ậ ủ
{ }
1,2,3, 4,5,6,7,8,9,10X=
.
a) Li t kê các ph n t c a ệ ầ ử ủ
( )
A B C� �
và
( )
D B C� �
;
b) Bi u di n các t p ể ễ ậ
{ }
5
,
{ }
4,6,10
,
{ }
2,8
theo
DCBA ,,,
.
Câu A 3.2: Trong t p ậ
{ }
2,3,6,9,12,13X=
xét hai hàm m nh đ ệ ề
( ) : " 10"P x x
và
( ) :Q x
”
x
l ”. Đt ẻ ặ
{ }
( )A x X P x=
,
{ }
( )B x X Q x=
. Hãy xác đnh các t p ị ậ
A
,
B
,
A B
,
A B
và
A B
.
Câu A 4.2: Ch ng minh r ng n u ứ ằ ế
ZYgYXf :,:
là hai song ánh thì ánh x h pạ ợ
g fo
cũng là m t song ánh và ộ
1 1 1
( )g f f g
− − −
=o o
.
Câu A 5.2: Trong t p s t nhiên khác không ậ ố ự
*
N
, xét quan h ệ
R
xác đnh b i: ị ở
a bR
khi và ch khi ỉ
a
chia h t cho ế
b
. Ch ng minh ứ
R
là m t quan h th t . ộ ệ ứ ự
R
là th t bứ ự ộ
ph n hay toàn ph n.ậ ầ
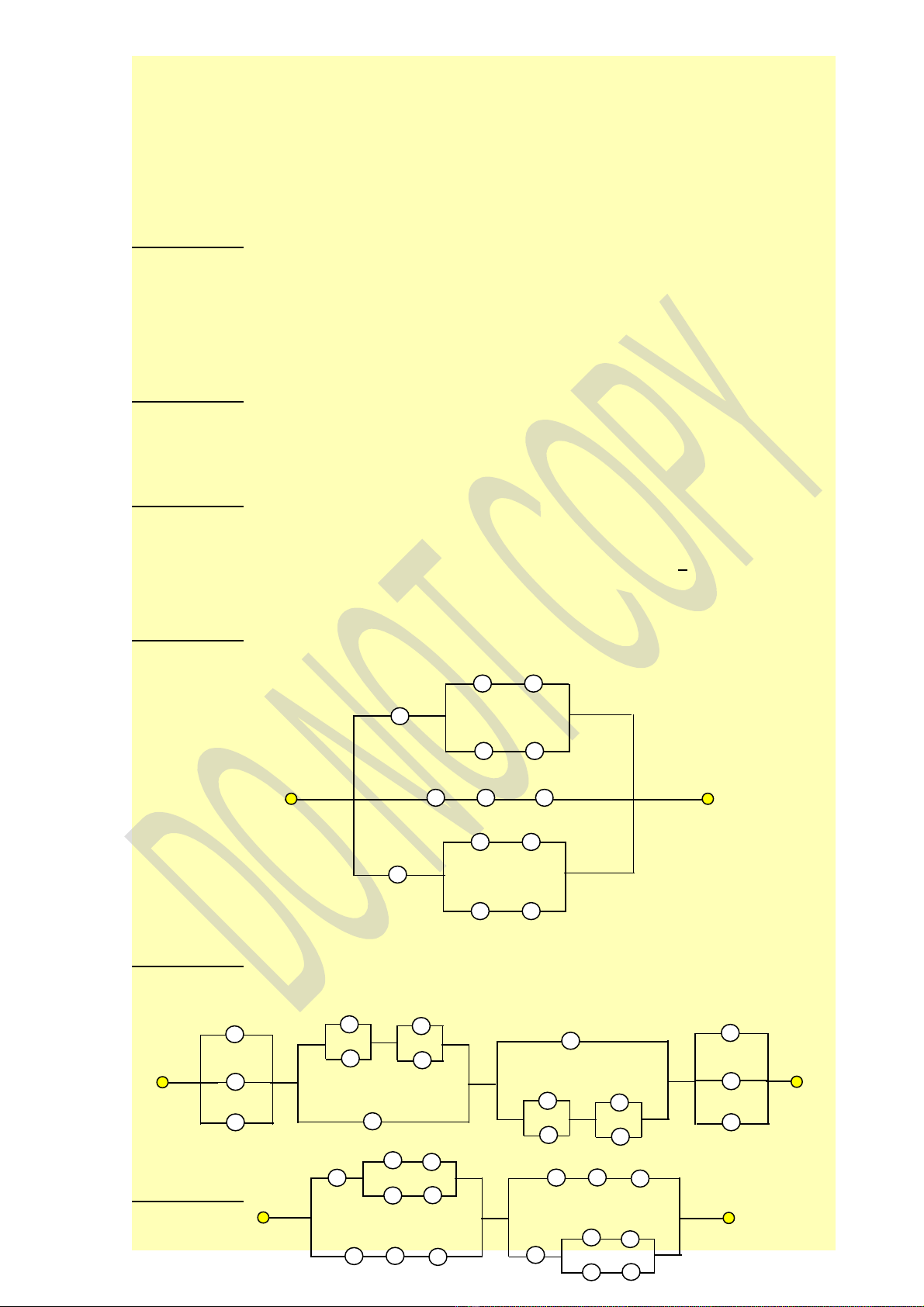
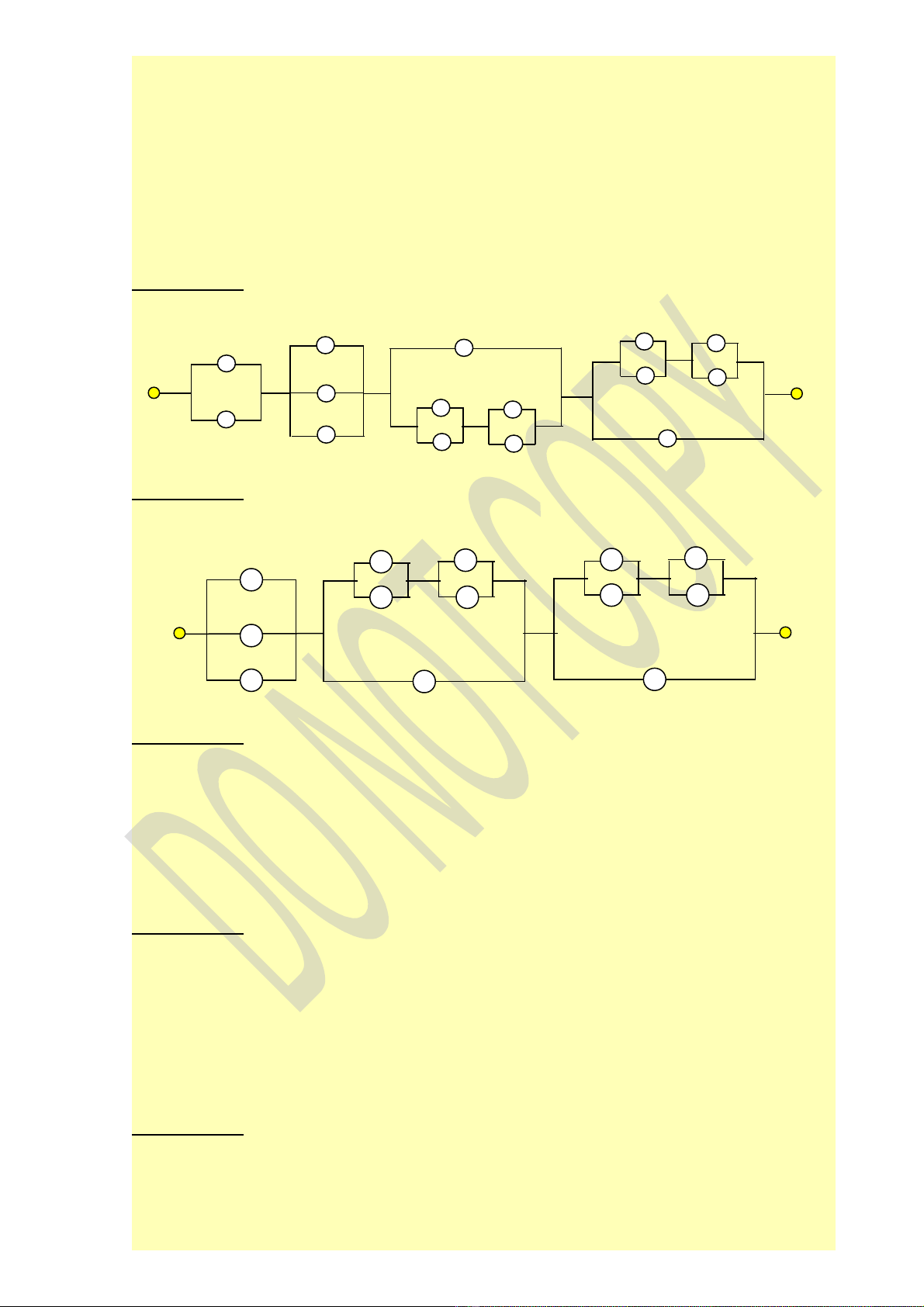
Câu A 6.2: Rút g n sau đó v s đ m ng c a công th c đi s Boole sau:ọ ẽ ơ ồ ạ ủ ứ ạ ố
( ) ( ') ( ' ') ( ' ') ( ' ' ')A x y z x y z x y z x y z x y z=��������������
1
Câu A 7.2: Rút g n sau đó v s đ m ng c a công th c đi s Boole sau:ọ ẽ ơ ồ ạ ủ ứ ạ ố
( ) ( )
{ }
{ } ( ) ( )
{ }
' ' ' 'A x z x z y x y z y z y z x=������������� � � �
� � � �
.
Câu A 8.2: Rút g n sau đó v s đ m ng c a công th c đi s Boole sau:ọ ẽ ơ ồ ạ ủ ứ ạ ố
{ } { } ( ) ( )
{ }
( ) ( )
{ }
' ' ' ' 'A x y x y z y z y z x x z x z y=������������������
� � � �
Câu A 9.2: Rút g n sau đó v s đ m ng c a công th c đi s Boole sau:ọ ẽ ơ ồ ạ ủ ứ ạ ố
{ } ( ) ( )
{ }
{ } ( ) ( )
{ }
' ' ' ' 'A y z x z x z y x y z y z y z x=��������������� � � �
� � � �
Câu A 10.2: Tìm hàm Boole
( , , )F x y z
nh n giá tr 1 khi và ch khi ậ ị ỉ
a)
0, 1, 1x y z= = =
; b)
1, 0y z= =
; c)
0, 1, 0x y z= = =
; d)
0x=
ho cặ
1, 1y z= =
.
Bi u di n m ng các chuy n m ch t ng ng v i k t qu tìm đc.ể ễ ạ ể ạ ươ ứ ớ ế ả ượ
Câu A 11.2: Ánh x ạ
:f? ?
có công th c xác đnh nh ứ ị ả
( ) 5 2f x x x= −
là đn ánh,ơ
toàn ánh, song ánh? Tìm công th c xác đnh nh c a ánh x ng c n u t n t i.ứ ị ả ủ ạ ượ ế ồ ạ
Câu A 12.2: Ánh x ạ
:f? ?
có công th c xác đnh nh ứ ị ả
3
( ) 5f x x= +
là đn ánh,ơ
toàn ánh, song ánh? Tìm công th c xác đnh nh c a ánh x ng c n u t n t i.ứ ị ả ủ ạ ượ ế ồ ạ
Câu A 13.2: Ánh x ạ
[ ] [ ]
: 1;1 1;3f− −
có công th c xác đnh nh ứ ị ả
2
( ) 2f x x x= −
là
đn ánh, toàn ánh, song ánh? Tìm công th c xác đnh nh c a ánh x ng c n u t n t i.ơ ứ ị ả ủ ạ ượ ế ồ ạ
Câu A 14.2: Trong
2
?
xét quan h ệ
( , ) ( ', ')x y x y
R
khi và ch khi ỉ
' 'x y x y+ = +
. Ch ngứ
minh
R
là m t quan h t ng đng. Bi u di n l p t ng đng c a (1,3) trong m tộ ệ ươ ươ ể ễ ớ ươ ươ ủ ặ
ph ng v i h t a đ tr c chu n ẳ ớ ệ ọ ộ ự ẩ
Oxy
.
Câu A 15.2: Trong
2
?
xét quan h ệ
1 2
1 1 2 2 1 2
1 2
( , ) ( , )
x x
x y x y x x
y y
<
=
. Ch ng minh quanứ
h ệ là quan h th t toàn ph n.ệ ứ ự ầ
Lo i 3 đi m ạ ể
Câu A 1.3: Ký hi u ệ
h g f=o
là h p c a hai ánh x ợ ủ ạ
ZYgYXf :,:
. Ch ngứ
minh:
a)
,f g
đn ánh thì ơ
h
đn ánh.ơ
b)
h
đn ánh thì ơ
f
đn ánh.ơ
c)
h
đn ánh và ơ
f
toàn ánh thì
g
đn ánh.ơ
d)
h
toàn ánh và
g
đn ánh thì ơ
f
toàn ánh.
Câu A 2.3: Ch ng minh r ng n u ứ ằ ế
f
đn ánh thìơ
2
a)
( ) ( )A B f A f B� � �
.
b)
)()()( BfAfBAf
.
c) Tìm ví d ch ng t r ng khi ụ ứ ỏ ằ
f
không đn ánh thì ơ
( ) ( )f A f B
nh ng ư
BA
và
)()()( BAfBfAf
.
Câu A 3.3: Cho ánh x ạ
:f X Y
.
a) Ch ng minh: ứ
1 1 1
, , ( ) ( ) ( )A B Y f A B f A f B
− − −
∀ ∆ = ∆�
,
trong đó
( ) ( )
\ \A B A B B A∆ =
hi u đi x ng c a ệ ố ứ ủ
A
và
B
.
b) Ch ng minh r ng ứ ằ
f
đn ánh khi và ch khi ơ ỉ
, , ( ) ( ) ( )A B X f A B f A f B∀ ∆ = ∆�
Câu A 4.3: Cho ánh x ạ
:f X Y
. Ch ng minh r ng quan h ứ ằ ệ
R
c a t p ủ ậ
X
xác đnhị
b i: ở
( ) ( )a b f a f b=�R
là m t quan h t ng đng. ộ ệ ươ ươ
Khi
X Y= = ?
và
( ) sinf x x=
, tìm l p t ng đng c a ớ ươ ươ ủ
a
.
Câu A 5.3: Trong t p s th c ậ ố ự , xét quan h ệ
R
xác đnh b i:ị ở
4 4 2 2
2( )x y x y x y− = −�R
.
Ch ng minh ứ
R
là m t quan h t ng đng. Tìm l p t ng đng ộ ệ ươ ươ ớ ươ ươ
a
c a ủ
a
.
Câu A 6.3: Rút g n m ng sau và v m ng đã rút g n:ọ ạ ẽ ạ ọ
Câu A 7.3: Rút g n m ng sau và v m ng đã rút g n:ọ ạ ẽ ạ ọ
Câu A 8.3: Rút g n m ng sau và v m ng đã rút g n:ọ ạ ẽ ạ ọ
3
z
'y
y
'z
z
y
x
w
y
'y
y
z
w
z
x
y
x
'y
y
'z
x
w
y
x
y
'w
w
'x
x
z
'z
'x
y
y
x
z
'y
y
z
'z
x
Câu A 9.3: Rút g n m ng sau và v m ng đã rút g n:ọ ạ ẽ ạ ọ
Câu A 10.3: Rút g n m ng sau và v m ng đã rút g n:ọ ạ ẽ ạ ọ
Câu A 11.3: Cho
, 'G G
là hai nhóm l n l t có ph n t trung hoà là ầ ượ ầ ử
e
và
'e
, ph n tầ ử
nh ch đo c a ị ả ủ
x
trong
G
là
1
x
−
và ph n t nh ch đo c a ầ ử ị ả ủ
y
trong
'G
là
1
y
−
.
: 'f G G
là m t đng c u nhóm. ộ ồ ấ
a) Ch ng minh: ứ
( ) 'f e e=
,
1 1
( ) ( )f a f a
− −
=
.
b) Ký hi u ệ
m
x
là tích
m
l n ph n t ầ ầ ử
x
, ch ng minh ứ
( ) ( )
m m
f a f a=
.
Câu A 12.3: Ch ng minh r ng trong nhóm ứ ằ
G
v i phép toán nhân:ớ
a) ph n t trung hòa c a ầ ử ủ
G
là duy nh t;ấ
b) m i ỗ
a G
có ph n t ngh ch đo duy nh t ầ ử ị ả ấ
1
a G
−
;
c)
( )
1
1
a a
−
−
=
và
( )
11 1
ab b a
−− −
=
;
d)
ab ac b c= =�
và
ba ca b c= =�
.
Câu A 13.3: Cho
, 'G G
là hai nhóm l n l t có ph n t trung hoà là ầ ượ ầ ử
e
và
'e
.
: 'f G G
là m t đng c u nhóm. Ta đnh nghĩa và kí hi u h t nhân c a đng c u nhómộ ồ ấ ị ệ ạ ủ ồ ấ
f
là
( )
1
Ker 'f f e
−
=
. Ch ng minh r ng:ứ ằ
4
'y
x
y
'x
z
x
y
z
z
'z
'x
x
y
z
x
y
'y
y
'z
x
y
'z
z
'x
'z
y
a)
Kerx f
khi và ch khi ỉ
1
Kerx f
−
,
1
x
−
là ph n t ngh ch đo c a ầ ử ị ả ủ x trong G.
b)
f
là đn c u khi và ch khi ơ ấ ỉ
ef Ker
.
Câu A 14.3: Cho vành
A
. Ch ng minh r ng, n u ứ ằ ế
,x y
là hai ph n t b t k c a vành ầ ử ấ ỳ ủ
A
tho mãn ả
yxxy
thì ta có nh th c Newton ị ứ
( )
0
n
nk k n k
n
k
x y x yC
−
=
+ =
đúng v i m i s tớ ọ ố ự
nhiên
n
, trong đó
1
0x
,
1
x x=
,
k
x
là tích k l n c a ph n t ầ ủ ầ ử
x
.
Câu A 15.3: Cho
A
là m t vành có đn v và ộ ơ ị
x A
. Gi s t n t i m t s t nhiênả ử ồ ạ ộ ố ự
0n
sao cho
0
n
x=
, ch ng minh r ng ứ ằ
a) t n t i ồ ạ
( )
11
1 1 ...
n
x x x
−−
− = + + +
.
b) t n t i ồ ạ
( )
11 1
1 1 ... ( 1)
n n
x x x
−− −
+ = − + + −
.
B. PH N 2 Ầ
Lo i 2 đi mạ ể
Câu B 1.2: Tìm đi u ki n c a ề ệ ủ
a
,
b
,
c
đ h ph ng trình sau có nghi mể ệ ươ ệ
2 3
2 6 11
2 7
x y z a
x y z b
x y z c
+ − =
+ − =
− + =
Câu B 2.2: Bi u di n ma tr n ể ễ ậ
4 1
3 3
A� �
=� �
− −
� �
theo t h p tuy n tính c a các ma tr n:ổ ợ ế ủ ậ
2 1
2 1
� �
� �
� �
,
7 1
1 1
� �
� �
� �
,
13 5
3 3
� �
� �
� �
,
5 2
2 4
� �
� �
� �
.
Câu B 3.2: Cho hai ma tr n ậ
và
6 2
12 8
B−
� �
=� �
� �
. Tìm ma tr n ậ
X
th a mãnỏ
AX B=
Câu B 4.2: Cho hai ma tr n ậ
5 3
4 2
A� �
=� �
� �
và
2 3
1 4
B� �
=� �
� �
. Tìm ma tr n ậ
X
th a mãnỏ
XA B=
Câu B 5.2: Tìm
1 2
W W
, trong đó:
{ }
1
( , ,0) ,W x y x y= ?
,
2
W
là không gian véc tơ
con c a ủ
3
?
sinh b i hai véc t ở ơ
(1,2,3)
và
(1, 1,1)−
.
Câu B 6.2: Gi s ả ử
,U V
và
W
là ba không gian véc t con c a m t không gian véc t .ơ ủ ộ ơ
Ch ng minh r ng ứ ằ
( ) ( ) ( )U V U W U V W+ +� � � �
.
5