PH N ẦI: XÁC SU TẤ
1. Bi n c ng u nhiên & xác su t c a bi n c :ế ố ẫ ấ ủ ế ố
1.1. Công th c c ng xác su t: ứ ộ ấ
1.1.1. p(A+B)=p(A)+p(B) (2 bi n c xung kh c)ế ố ắ
1.1.2. p(A+B)=p(A)+p(B)-p(A.B) p(A+B+C)=p(A)+p(B)+p(C)-[p(AB)+p(AC)+p(BC)]
+p(ABC)
1.2. Công th c nhân xác su t:ứ ấ
1.2.1. p(A.B)=p(A).p(B) (2 bi n c đ c l p)ế ố ộ ậ
1.2.2. p(A.B)=p(A).p(B/A)
1 2 1 2 1 1 2 1
( ... ) ( ). ( / )... ( / .. )
n n n
p A A A p A p A A p A A A A
−
=
1.3. Công th c Bernoulli: cho 2 bi n c A và ứ ế ố
A
1.3.1.
( )
x x n x
n n
p x C p q
−
=
, p=p(A), q=1-p
1.4. Công th c xác su t đ y đ :ứ ấ ầ ủ
1 1 2 2
( ) ( ). ( / ) ( ). ( / ) ... ( ). ( / )
n n
p F p A p F A p A p F A p A p F A= + + +
1.5. Công th c Bayes: ứ
( . ) ( ). ( / )
( / ) ( ) ( )
i i i
i
p A F p A p F A
p A F p F p F
= =
2. Bi n ng u nhiên:ế ẫ
2.1. B ng phân ph i xác su t (bi n ng u nhiên r i r c) ả ố ấ ế ẫ ờ ạ
2.2. Hàm m t đ xác su t (ậ ộ ấ
( )f x
) (bi n ng u nhiên liên t c)ễ ẫ ụ
2.2.1.
( )f x
≥
0
2.2.2.
( ) 1f x dx
+∞
−∞
=
∫
2.2.3.
2.3. Hàm phân ph i xác su t (ố ấ
( )F x
) (dùng cho c 2 lo i bi n-th ng là bi n ng uả ạ ế ườ ế ẫ
nhiên liên t c)ụ
2.3.1.
( )F x
=p(
F
<x)
2.3.2.
'( ) ( )F x f x=
2.3.3.
( ) ( )
x
F x f t dt
−∞
=∫
2.4. Kỳ v ng ọ
2.4.1.
1 1 2 2
( ) ...
n n
E x x p x p x p= + + +
(t b ng phân ph i xác su t)ừ ả ố ấ
2.4.2.
( ) ( )E x xf x dx
+∞
−∞
=∫
2.5. Ph ng sai:ươ
2.5.1.
2 2
( ) ( ) [ ( )]V x E x E x= −
2.5.2.
2 2
( ) ( ) [ ( ) ]V x x f x dx xf x dx
+∞ +∞
−∞ −∞
= −
∫ ∫
3. M t s phân ph i xác su t thông d ng:ộ ố ố ấ ụ
3.1. Phân ph i chu n t ng quát: ố ẩ ổ
2
~ ( ; )X N
µ σ
3.1.1.
2
2
( )
2
1
( ) 2
x
f x e
µ
σ
σ π
−
−
=
3.1.2.
( ) 1f x dx
+∞
−∞
=
∫
3.1.3.
ModX MedX
µ
= =
;
2
( ) , ( )E x V x
µ σ
= =
3.1.4.
( ) ( ) ( )
b a
p a x b
µ ϕ
ϕ ϕ
σ σ
− −
≤ ≤ = −
3.1.5. Phân ph i chu n t c ố ẩ ắ
2
0, 1
µ σ
= =
3.1.5.1.
~ (0,1)T N
3.1.5.2.
2
2
1
( ) 2
t
f t e
π
−
=
3.1.5.3. Đ i bi n ổ ế
X
T
µ
σ
−
=
3.1.5.4.
( ) ( ) ( )p a x b b a
ϕ ϕ
≤ ≤ = −
3.2. Phân ph i Poisson: ố
~ ( )X P
λ
,
λ
>0
3.2.1.
( ) !
k
p k e k
λ
λ
λ
−
= =
3.2.2.
( ) ( )E x V x
λ
= =
3.3. Phân ph i nh th cố ị ứ :
~ ( , )X B n p
3.3.1.
( ) ( ) , 1
k k n k
n n
p X k p k C p q p q
−
= = = + =
3.3.2.
0
( ) 1
n
k
p X k
=
= =
∑
3.3.3.
( )E x np=
,
0 0
,ModX x np q x np q= − ≤ ≤ +
3.3.4. Khi n=1:
~ (1, )X B p
:phân ph i không-m tố ộ
3.3.4.1.
2
( ) , ( ) , ( )E x p E x p V x pq= = =
3.3.5. X p x phân ph i nh th c:ấ ỉ ố ị ứ
3.3.5.1. B ng phân ph i Poisson:ằ ố
n
>50,
p
<0.1;
~ ( , ) ~ ( )X B n p X P
λ
≈
,
np
λ
=
.
( ) !
k
k k n k
n
p x k C p q e k
λ
λ
− −
= = =
3.3.5.2. B ng phân ph i chu n: ằ ố ẩ
0.5, 0.5, ,np nq np npq
µ σ
≥ ≥ = =
.
~ ( , ) ~ ( , )X B n p X N np npq≈
1
( ) ( )
k
p x k f
µ
σ σ
−
= =
; p(
1
k
<X<
2 1
2
) ( ) ( )
k k
k
µ µ
ϕ ϕ
σ σ
− −
= −
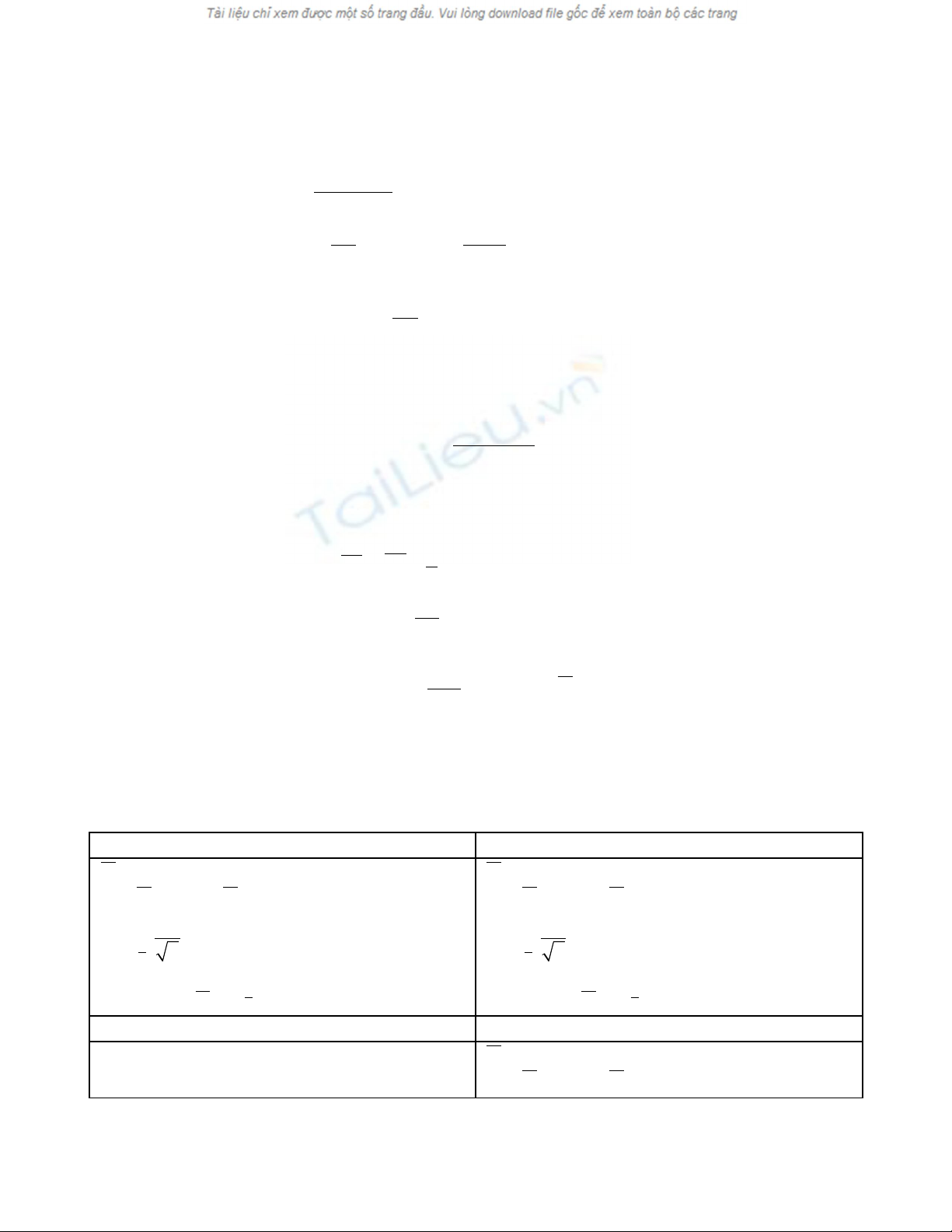
3.4. Phân ph i siêu b i:ố ộ
~ ( , , )
A
X H N N n
[N:t ng s ph n t , ổ ố ầ ử
A
N
:S ph n t cóố ầ ử
tính ch t A trong N, n: s ph n t l y ng u nhiên].G i X là s ph n t có tính ch t Aấ ố ầ ử ấ ẫ ọ ố ầ ử ấ
trong n.
.
( )
A A
k n k
N N N
n
N
C C
p X k C
−
−
= =
3.4.1.
( ) ,
A
N
E X np p N
= =
;
( ) . , 1
1
N n
V X npq q p
N
−
= = −
−
3.4.2. X p x phân ph i siêu b i b ng phân ph i nh th c: ấ ỉ ố ộ ằ ố ị ứ
0.05 ~ ( , )n N X B n p≤ ⇒
;
( ) ,
k k n k A
n
N
p X k C p q p N
−
= = =
3.5. Bi n ng u nhiên 2 chi u: X ế ẫ ề và Y đ c l pộ ậ
( ). ( )
ij i j
P p x q y⇔ =
v i m i i,jớ ọ
3.6.Hi p ph ng sai và h s t ng quan:ệ ươ ệ ố ươ
3.6.1. Hi p ph ng sai(cov): ệ ươ
cov( , ) ( ) ( ) ( )X Y E XY E X E Y= −
3.6.2. H s t ng quanệ ố ươ
,X Y
ρ
:
,
cov( , )
( ) ( )
X Y
X Y
X Y
ρσ σ
=
PH N 2: TH NG KÊẦ Ố
1. T ng th và m uổ ể ẫ
1.1. Th c hành tính toán trên m u:ự ẫ
1.1.1. Tính trung bình (
n
X
):
1
1
n
n i
i
X x
n
=
=∑
1.1.2. Tính t l m u: (ỷ ệ ẫ
n
f
);
A
n
m
fn
=
(
A
m
:s ph n t mang tính ch t A; n: kích th cố ầ ử ấ ướ
m u)ẫ
1.1.3. Tính ph ng sai m u:ươ ẫ
2 2 2
1
1[ ( ) ]
1
k
i i
S n x n X
n
= −
−∑
1.2. c l ng tham s c a t ng th : Ướ ượ ố ủ ổ ể
1.2.1. c l ng đi m: Ướ ượ ể
2 2
( ) , ( ) , ( )
n n
E X E f p E S
µ σ
= = =
1.2.2. c l ng kho ng:Ướ ượ ả
1.2.2.1. c l ng kho ng cho trung bình: V i đ tin c y 1-Ướ ượ ả ớ ộ ậ
α
cho tr c, 1 m uướ ẫ
kích th c n.ướ
30n≥
,
2
σ
bi tế
30n≥
,
2
σ
ch a bi tư ế
X
,
σ
1 2
,X X
µ ε µ ε
= − = +
2
.un
α
σ
ε
=
(
1
α
−
0.5-
2
α
2
u
α
)
X
,s
1 2
,X X
µ ε µ ε
= − = +
2
.s
un
α
ε
=
(
1
α
−
0.5-
2
α
2
u
α
)
n
<30,
2
σ
bi tế
n
<30,
2
σ
ch a bi tư ế
Nh TH1ư
X
,s
1 2
,X X
µ ε µ ε
= − = +
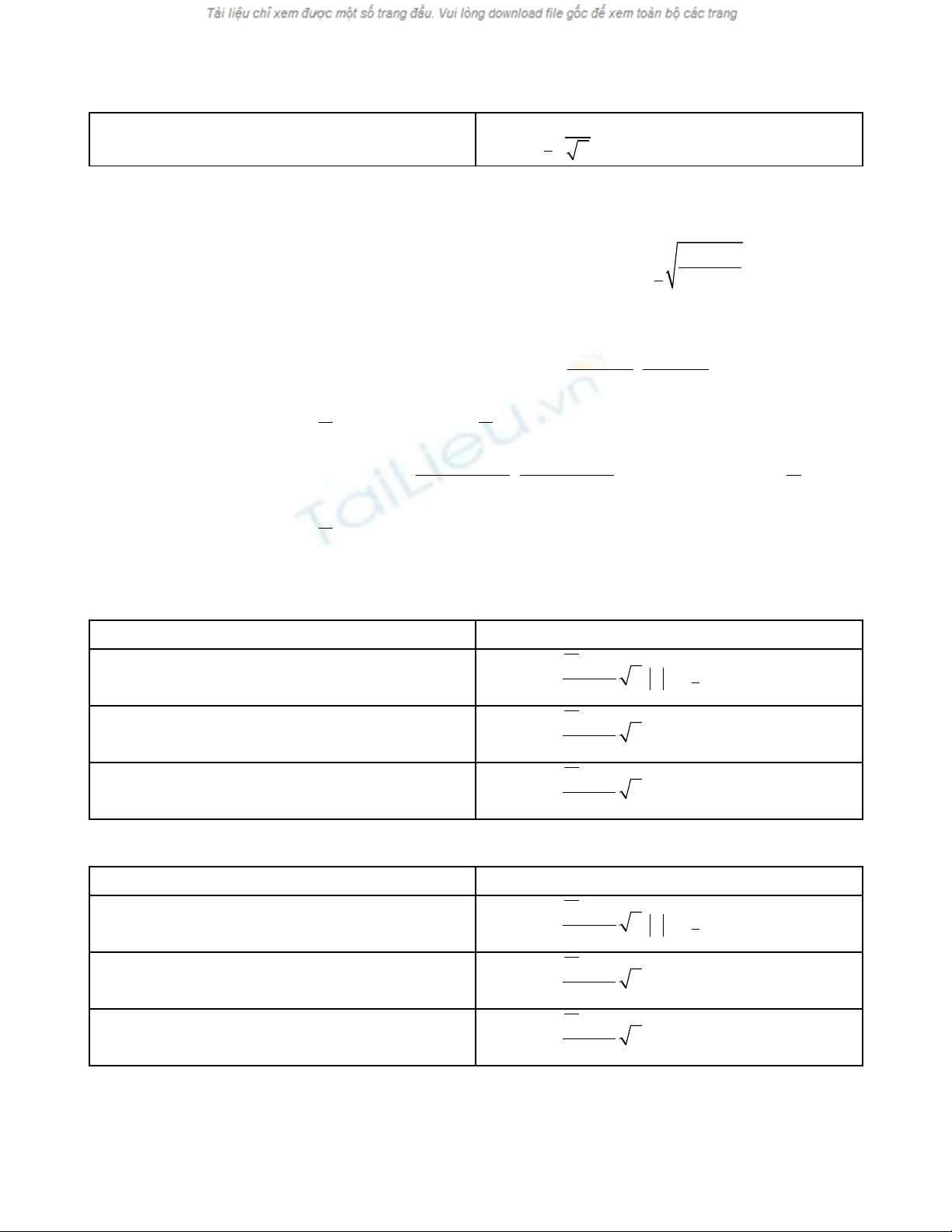
( 1, )
2
.
n
s
tn
α
ε
−
=
1.2.2.2. c l ng kho ng cho t l : t ng th có t l p ch a bi t, v i đ tin c yƯớ ượ ả ỷ ệ ổ ể ỷ ệ ư ế ớ ộ ậ
1
α
−
cho tr c, v i 1 m u kích th c n, t l m u ướ ớ ẫ ướ ỷ ệ ẫ
n
f
. Tìm 2 s ố
1 2
,p p
tho :ả
1 2
( ) 1p p p p
α
≤ ≤ = −
,
1,2 n
p f
ε
=m
Công th c: ứ
2
(1 )f f
un
α
ε
−
=
1.2.2.3. c l ng kho ng cho ph ng sai:Gi s t ng th có Ướ ượ ả ươ ả ử ổ ể
2
σ
ch a bi t. D aư ế ự
vào 1 m u kích th c n, v i đ tin c y 1-ẫ ướ ớ ộ ậ
α
cho tr c.ướ
TH1:
µ
ch a bi t, bi t ư ế ế
2
S
. Khi đó ta có
2 2
2
2 2
1 2
( 1) ( 1)
[,]
n S n S
σχ χ
− −
∈
trong đó
2 2
1
( 1, )
2
n
α
χ χ
= −
,
2 2
2
( 1,1 )
2
n
α
χ χ
= − −
TH2:
µ
bi t. Khi đó ế
2
2 2
1 2
( ) ( )
[ , ]
i i i i
n x n x
µ µ
σχ χ
− −
∈∑ ∑
, trong đó
2 2
1
( , )
2
n
α
χ χ
=
,
2 2
2
( ,1 )
2
n
α
χ χ
= −
1.2.3. Ki m đ nh gi thuy t th ng kê:ể ị ả ế ố
1.2.3.1. Ki m đ nh gi thuy t th ng kê cho ể ị ả ế ố
µ
1.2.3.1.1. TH1:
2
σ
bi tế
Gi thuy t th ng kêả ế ố
W
α
:
2
σ
bi tế(mi n bác b ề ỏ
0
H
)
0 0
:H
µ µ
=
1
:H
µ
≠
0
µ
0
{ ,
X
W u n u
α
µ
σ
−
= =
>
2
u
α
}
0 0
:H
µ µ
=
1
:H
µ
<
0
µ
0
{X
W u n
α
µ
σ
−
= =
,u<-
u
α
}
0 0
:H
µ µ
=
1
:H
µ
>
0
µ
0
{X
W u n
α
µ
σ
−
= =
,u>
u
α
}
1.2.3.1.2. TH2:
30n
≥
,
2
σ
không bi tế
Gi thuy t th ng kêả ế ố
W
α
(mi n bác b ề ỏ
0
H
)
0 0
:H
µ µ
=
1
:H
µ
≠
0
µ
0
{ ,
X
W u n u
s
α
µ
−
= =
>
2
u
α
}
0 0
:H
µ µ
=
1
:H
µ
<
0
µ
0
{X
W u n
s
α
µ
−
= =
,u<-
u
α
}
0 0
:H
µ µ
=
1
:H
µ
>
0
µ
0
{X
W u n
s
α
µ
−
= =
,u>
u
α
}
1.2.3.1.3. TH3:
n
<30,
2
σ
không bi tế
Gi thuy t th ng kêả ế ố
W
α
(mi n bác b ề ỏ
0
H
)
0 0
:H
µ µ
=
1
:H
µ
≠
0
µ
0
{ ,
X
W t n t
s
α
µ
−
= =
>
( 1, )
2
n
t
α
−
}
0 0
:H
µ µ
=
1
:H
µ
<
0
µ
0
{X
W t n
s
α
µ
−
= =
,
t
<-
( 1, )
2
n
t
α
−
}
0 0
:H
µ µ
=
1
:H
µ
>
0
µ
0
{ ,
X
W t n
s
α
µ
−
= =
t
>
( 1, )
2
n
t
α
−
}
1.2.3.2. Ki m đ nh gi thuy t th ng kê cho t l :ể ị ả ế ố ỷ ệ
Gi thuy t th ng kêả ế ố
W
α
(mi n bác b ề ỏ
0
H
)
0: 0
H p p=
1:
H p
≠
0
p
0
0 0
{ ,
(1 )
f p
W u u
p p
n
α
−
= = −
>
2
u
α
}
0: 0
H p p=
1:
H p
<
0
p
0
0 0
{(1 )
f p
W u p p
n
α
−
= = −
,
u
<-
u
α
}
0: 0
H p p=
1:
H p
>
0
p
0
0 0
{(1 )
f p
W u p p
n
α
−
= = −
,
u
>
u
α
}
1.2.3.3. Ki m đ nh gi thuy t th ng kê cho ph ng sai:ể ị ả ế ố ươ
1.2.3.3.1. TH1:
µ
ch a bi tư ế
Gi thuy t th ng kêả ế ố
W
α
(mi n bác b ề ỏ
0
H
)
2 2
0 0
:H
σ σ
=
2
1
:H
σ
≠
2
0
σ
2
2
2
0
( 1)
{n s
W
α
χσ
−
= =
,
2
χ
<
2
1
χ
ho c ặ
2
χ
>
2
2
χ
2 2 2 2
1 2
( 1,1 ) ( 1, )
2 2
,
n n
α α
χ χ χ χ
− − −
= =
2 2
0 0
:H
σ σ
=
2
1
:H
σ
<
2
0
σ
2
2
2
0
( 1)
{n s
W
α
χσ
−
= =
,
2
χ
<
2
( 1,1 )n
α
χ
− −
2 2
0 0
:H
σ σ
=
2
1
:H
σ
>
2
0
σ
2
2
2
0
( 1)
{n s
W
α
χσ
−
= =
,
2
χ
>
2
( 1, )n
α
χ
−
1.2.3.3.2. TH2:
µ
bi t.ế
Gi thuy t th ng kêả ế ố
W
α
(mi n bác b ề ỏ
0
H
)
2 2
0 0
:H
σ σ
=
2
1
:H
σ
≠
2
0
σ
2
2
2
0
( )
{
i i
n x
W
α
µ
χσ
−
= = ∑
,
2
χ
<
2
1
χ
ho c ặ
2
χ
>
2
2
χ
2 2 2 2
1 2
( ,1 ) ( , )
2 2
,
n n
α α
χ χ χ χ
−
= =