PHÂN TÍCH
CÁC GI I THU T S P X PẢ Ậ Ắ Ế
1
Nội dung
Giải thuật Insertion-Sort
Các giải thuật chia để trị
Giải thuật Quicksort
Giải thuật Mergesort
Giải thuật HeapSort
Giải thuật Couting Sort
2
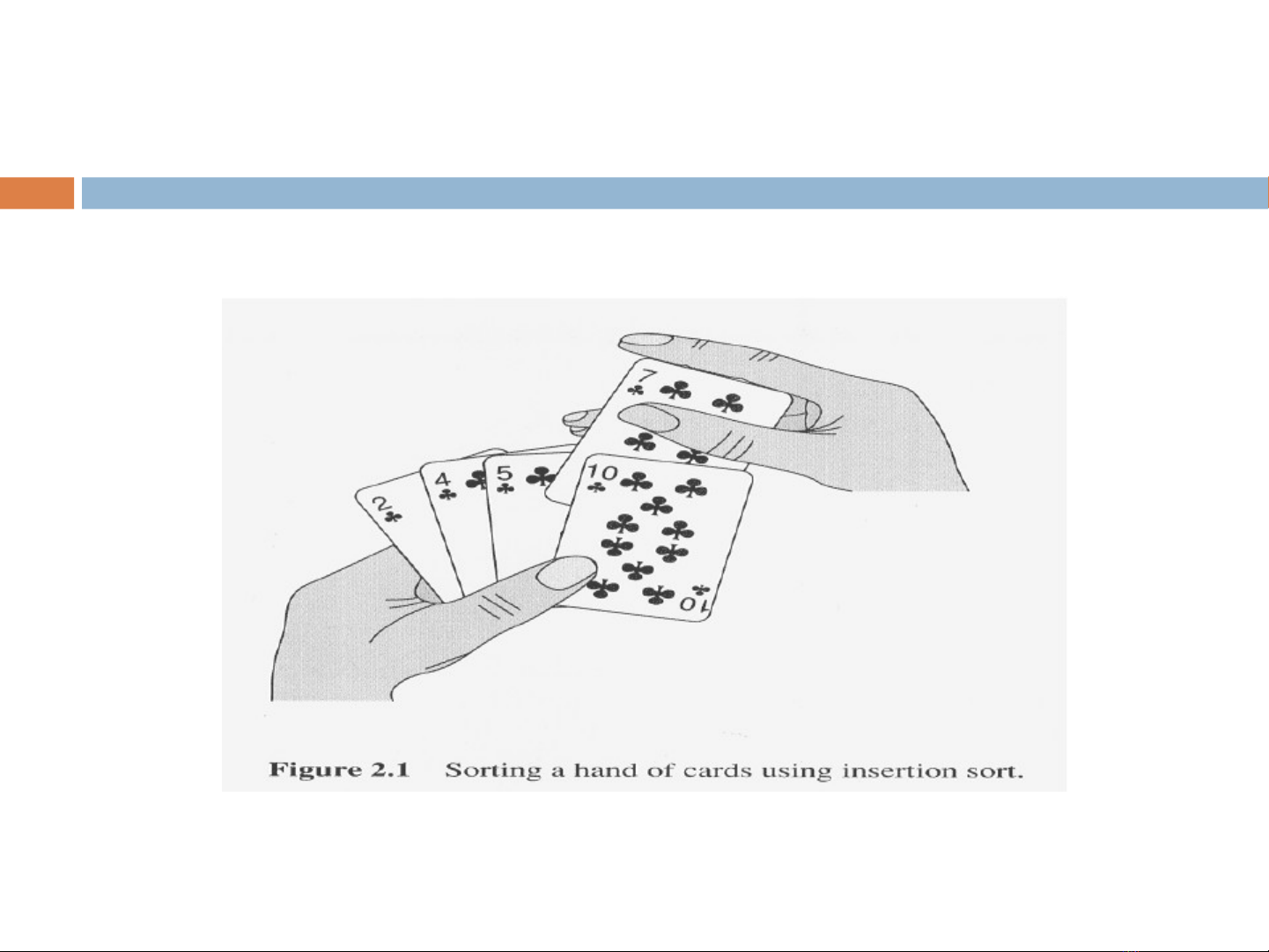
Insertion Sort
3
DEMO_HUNG
Insertion Sort – Ý t ngưở
Nh n xét:ậ
M i dãy ọa[0] , a[1] ,..., a[n-1] luôn có i-1 ph n t đ u tiên ầ ử ầ a[0] ,
a[1] ,... , a[i-2] đã có th t (i ≥ 2)ứ ự
Ý t ng chính: ưở
Tìm cách chèn ph n t ầ ử a[i] vào v trí thích h p c a đo n đã ị ợ ủ ạ
đ c s p đ có dãy m i ượ ắ ể ớ a[0] , a[1] ,... , a[i-1] tr nên có th tở ứ ự
V trí này chính là pos th a :ị ỏ
a[pos-1] ≤ a[i ]< a[pos] (1≤pos≤i)
4
Chương 4: Sắp xếp
Insertion Sort – Ví dụ
2 8 5 1 6 4 1512
1 2 3 4 5 6 70
5
Chương 4: Sắp xếp