
Đ
Đạ
ại H
i Họ
ọc Sư Ph
c Sư Phạ
ạm Tp. H
m Tp. Hồ
ồCh
Chí
íMinh
Minh
Chương 2: Tìm kiếm & Sắp xếp
C
CẤ
ẤU TR
U TRÚ
ÚC D
C DỮ
ỮLI
LIỆ
ỆU 1
U 1
2
2
Tìm kiếm & Sắp xếp
Muïc tieâu:
•Giôùi thieäu moät soá thuaät toaùn tìm kieám vaø saép xeáp noäi.
•Phaân tích, ñaùnh giaù ñoä phöùc taïp cuûa caùc giaûi thuaät tìm
kieám, saép xeáp.
Noäi dung:
•Nhu caàu tìm kieám vaø saép xeáp döõ lieäu trong moät heä
thoáng thoâng tin.
•Caùc giaûi thuaät tìm kieám noäi.
•Caùc giaûi thuaät saép xeáp noäi.
3
3
Caùc giaûi thuaät
tìm kieám noäi
•Tìm tuần tự
•Tìm nhị phân
Tìm kiếm
4
4
Caùc giaûi thuaät tìm kieám noäi
Baøi toaùn: Tìm vò trí xuaát hieän cuûa phaàn töû coù
giaù trò x treân danh saùch ñaëc a
•Taäp döõ lieäu ñöôïc löu tröõ laø daõy soá a
1
, a
2
, ... ,a
N
int a[N];
•Khoaù caàn tìm laø x
int x;
5
5
Tìm kieám tuaàn töï
•Böôùc 1: i = Vò trí ñaàu;
•Böôùc 2: Neáu a[i] = x : Tìm thaáy. Döøng, vò trí
xuaát hieän: i
•Böôùc 3 : i = Vò trí keá(i);// xeùt tieáp phaàn töû keá
trong maûng
•Böôùc 4: Neáu i >Vò trí cuoái: //Heát maûng
Khoâng tìm thaáy. Döøng.
Ngöôïc laïi: Laëp laïi Böôùc 2.
6
6
Tìm kieám tuaàn töï
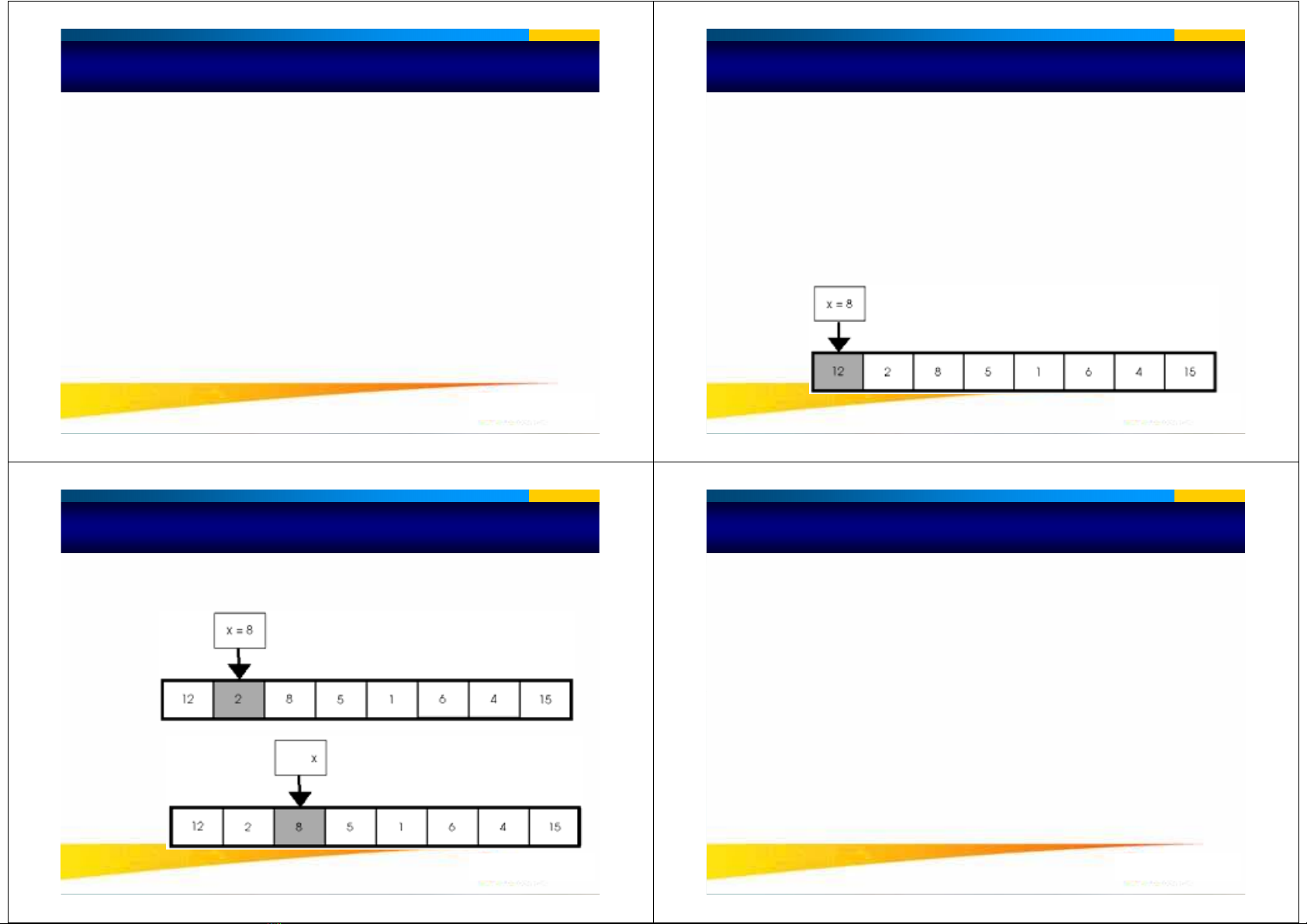
•Ví duï: Cho daõy soá a
1228516415
•Giaù trò caàn tìm: 8
•i = 1
7
7
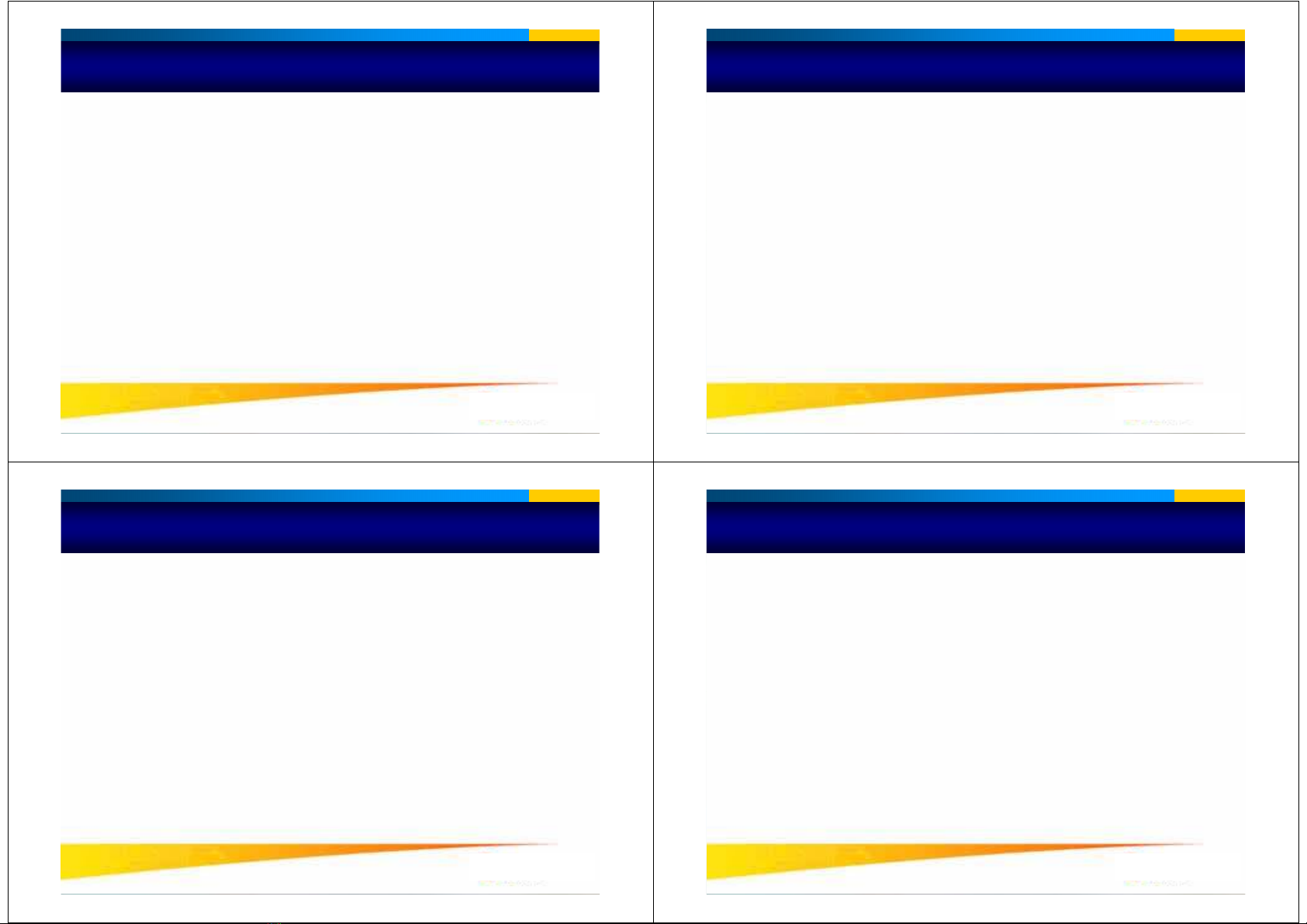
Tìm kieám tuaàn töï
•i = 2
•i = 3
8
8
T
TT
Tì
ìì
ìm kie
m kiem kie
m kieáááám tua
m tuam tua
m tuaààààn t
n tn t
n töï
öïöï
öï
int LinearSearch(int a[], int N, int x)
{
for (int i=0; (i<N)&&(a[i]!=x ); i++);
if (i<N)
return i; // a[i] laø phaàn töû coù khoaù x
return -1; // tìm heát maûng nhöng khoâng coù x
}

9
9
Tìm kieám tuaàn töï
•Caûi tieán caøi ñaët: duøng phöông phaùp “đặt lính
canh”
–Ñaët theâm moät phaàn töû coù giaù trò x vaøo cuoái maûng
–Baûo ñaûm luoân tìm thaáy x trong maûng
–Sau ñoù döïa vaøo vò trí tìm thaáy ñeå keát luaän.
10
10
Tìm kieám tuaàn töï
int LinearSearch(int a[], int N, int x)
{
// maûng goàm N phaàn töû töø a[0]..a[N-1]
a[N] = x; // theâm lính canh vaøo cuoái daõy
for (int i=0; (a[i]!=x); i++);
if (i<N)
return i; // a[i] laø phaàn töû coù khoaù x
return -1; // tìm heát maûng nhöng khoâng coù x
}
11
11
Tìm kieám tuaàn töï
•Ñaùnh giaù giaûi thuaät:
•Vaäy giaûi thuaät tìm tuaàn töï coù ñoä phöùc taïp
tính toaùn caáp n: T(n) = O(n)
12
12
Tìm kieám tuaàn töï
Nhaän xeùt:
–Giaûi thuaät tìm tuyeán tính khoâng phuï thuoäc vaøo
thöù töï cuûa caùc phaàn töû trong danh saùch, do vaäy
ñaây laø phöông phaùp toång quaùt nhaát ñeå tìm kieám
treân moät danh saùch baát kyø.
–Moät thuaät toaùn coù theå ñöôïc caøi ñaët theo nhieàu
caùch khaùc nhau, kyõ thuaät caøi ñaët aûnh höôûng ñeán
toác ñoä thöïc hieän cuûa thuaät toaùn.
13
13
Tìm kieám nhò phaân
•Ñoái vôùi nhöõng daõy ñaõ sắp thöù töï (giaû söû thöù töï
taêng), caùc phaàn töû trong daõy coù quan heä
a
i -1
≤
≤≤
≤a
i
≤
≤≤
≤a
i+1
Neáu x > a
i
thì x chæ coù theå xuaát hieän trong
ñoaïn [a
i+1
,a
N
]cuûa daõy
Neáu x < a
i
thì x chæ coù theå xuaát hieän trong
ñoaïn [a
1
,a
i-1
]cuûa daõy
14
14
Tìm kieám nhò phaân
•YÙ töôûng cuûa giaûi thuaät laø taïi moãi böôùc tieán
haønh so saùnh xvôùi phaàn töû naèm ôû vò trí giöõa
cuûa daõy tìm kieám hieän haønh, döïa vaøo keát quaû
so saùnh naøy ñeå quyeát ñònh giôùi haïn daõy tìm
kieám ôû böôùc keá tieáp laø nöûa treân hay nöûa döôùi
cuûa daõy tìm kieám hieän haønh
15
15
Tìm kieám nhò phaân
Böôùc 1: left = VTÑ; right = VTC;
Böôùc 2: Trong khi left ≤
≤≤
≤right laëp: //ñoaïn tìm kieám chöa roãng
Böôùc 2.1: mid = (left+right)/2; // laáy moác so saùnh
Böôùc 2.2: Neáu a[mid] = x: //Tìm thaáy.
Döøng, vò trí xuaát hieän: mid
Böôùc 2.3: Neáu a[mid] > x: //tìm x trong daõy con a
left
.. a
mid -1
right = mid - 1;
Ngöôïc laïi //tìm x trong daõy con a
mid +1
.. a
right
left = mid + 1;
//Heát laëp
Böôùc 3: Döøng, khoâng tìm thaáy.
16
16
Tìm kieám nhò phaân
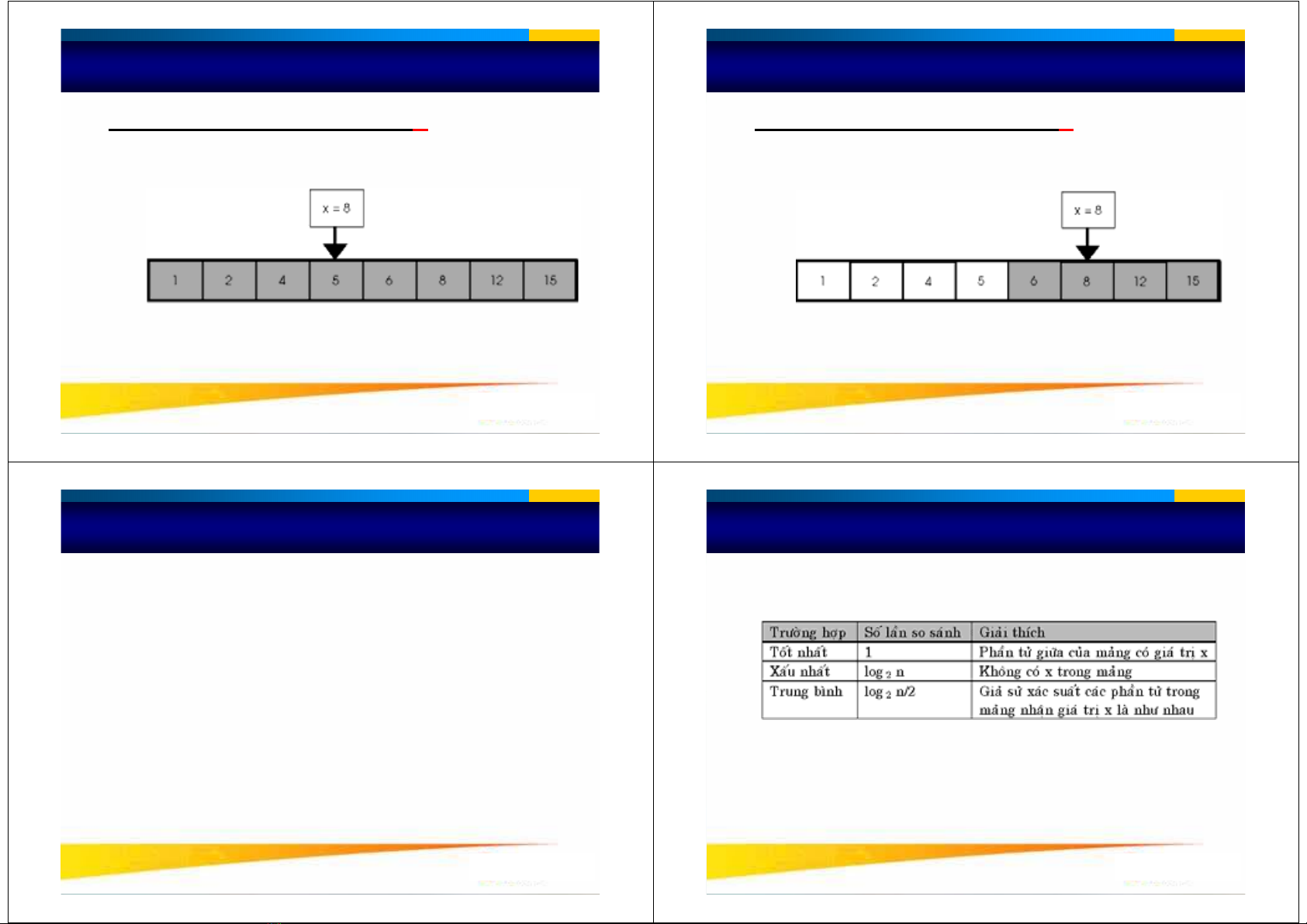
•Ví duï: Cho daõy soá a goàm 8 phaàn töû:
1245 6 8 12 15
•Giaù trò caàn tìm laø 8
17
17
Tìm kieám nhò phaân
•left = 1, right = 8, mid = 4
18
18
Tìm kieám nhò phaân
•left = 5, right = 8, mid = 6
19
19
Tìm kieám nhò phaân
int BinarySearch(int a[],int N,int x )
{
int left =0, right = N-1, midle;
while (left <= right)
{
midle = (left + right)/2;
if (x == a[midle])
return midle;//Tìm thaáy x taïi mid
if (x<a[midle])right = midle -1;
else left = midle +1;
}
return -1; // trong daõy khoâng coù x
}
20
20
Tìm kieám nhò phaân
•Ñaùnh giaù giaûi thuaät:
•Giaûi thuaät tìm nhò phaân coù ñoä phöùc taïp
tính toaùn caáp logn:
T(n) = O(log
2
n)


























