Goi k la sô điêm c c tri cua ham sô y = f(x); h la sô nghiêm đn cua ph ng trinh ư ơ ươ
f(x) = 0; e la sô nghiêm bôi le cua ph ng trinh f(x) = 0, ươ
thi sô điêm c c tri cua ham sô băng k + h + e ư
Đ ch ng minh nh n xét trên, tr c tiên ta ch ng minh b đ sau: ể ứ ậ ướ ứ ổ ề
B đổ ề: N u là đi m t i h n c a hàm s y = f(x) thì cũng là đi m t i h n c a hàm sế ể ớ ạ ủ ố ể ớ ạ ủ ố
g(x)=| f(x)|
Ch ng minh b đ: ứ ổ ề
+ Ta có
+ Theo gi thi t, là đi m t i h n c a hàm s ả ế ể ớ ạ ủ ố nên xác đnh và không xác đnh.ị ị
+) Ta có . Vì xác đnh nên xác đnh. V y ị ị ậ xác đnh. (*)ị
+ Ta có . Vì không xác đnh nênkhông xác đnh. V y không xác đnh.(**)ị ị ậ ị
T (*), (**) suy ra cũng là đi m t i h n c a hàm s g(x)=| f(x)|ừ ể ớ ạ ủ ố
Ch ng minh nh n xét 1ứ ậ
Thât vây
+ Theo gi thi t, y = f(x) co k điêm c c tri co m nghiêm đn, n nghiêm bôi le và t đi m t i ả ế ư ơ ể ớ
h n ma m + n + t = k. (*)ạ
+ Theo gi thi t, h la sô nghiêm đn cua ph ng trinh ; e la sô nghiêm bôi le cua ph ng ả ế ơ ươ ươ
trinh (**)
+ ;
Theo (*), (**) ta co sô điêm c c tri cua ham sô băng k + h + e ư
Nhân xet 2: Sô điêm c c tri cua ham sô băng sô điêm c c tri cua ham sô y = f(x). ư ư
Th t v yậ ậ
+) Theo gi thi t y = f(x) co k điêm c c tri co m nghiêm đn, n nghiêm bôi le và t đi m t i ả ế ư ơ ể ớ
h n ma m + n + t = k. Gia s cac nghiêm đo la ạ ư
+) co;co k giá tr (g m nghiêm đn, nghi m bôi le, đi m t i h n). Vây co k điêm c c tri. ị ồ ơ ệ ể ớ ạ ư
Hay sô điêm c c tri cua ham sô băng sô điêm c c tri cua ham sô y = f(x). ư ư
1.1.Bai toan c ban: “ ơ Cho hàm s . H i sô đi m c c tr c a hàm s ”ố ỏ ể ự ị ủ ố
Bai 1:
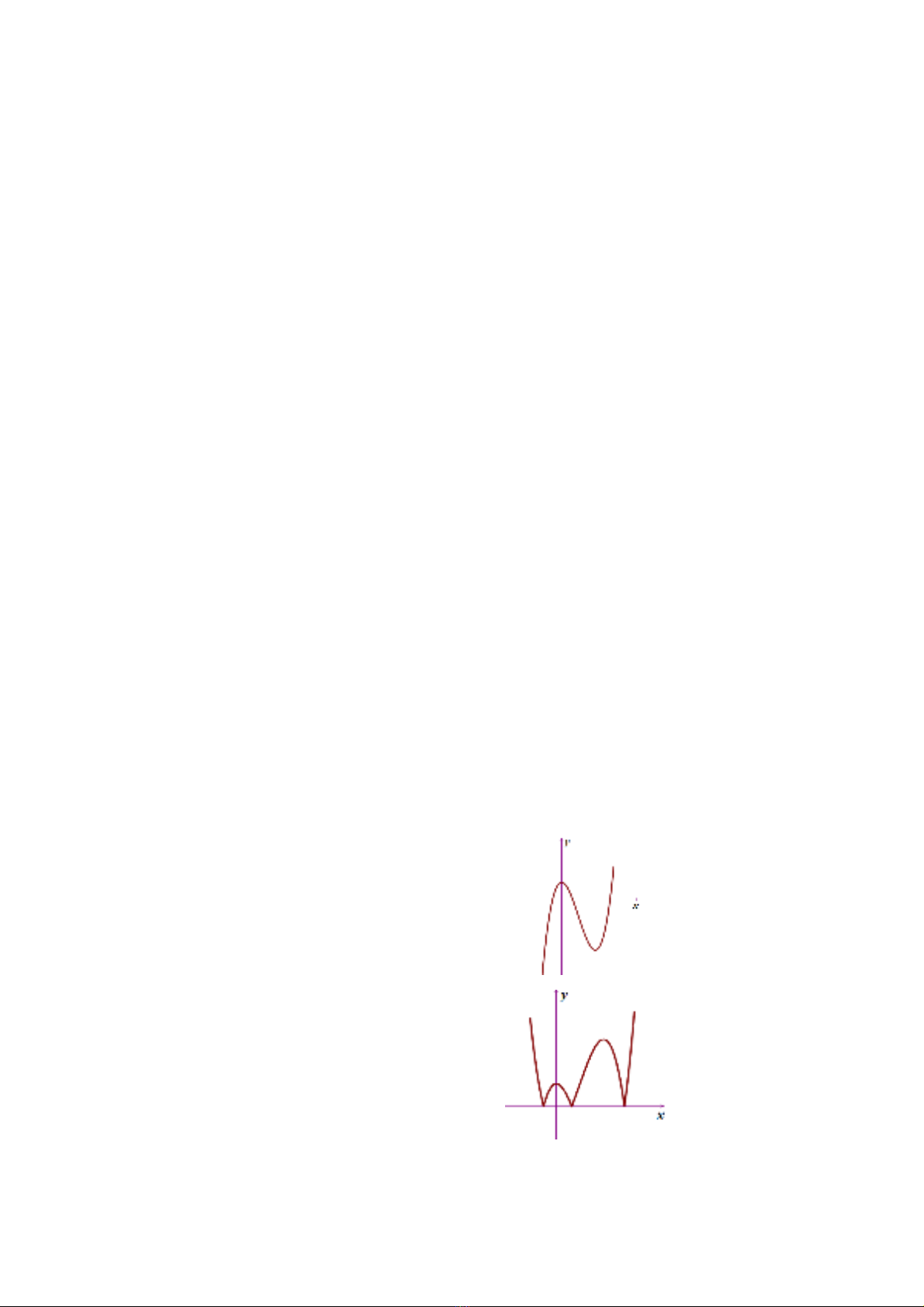
Cho ham sô co đô thi (C) nh hinh ve. Tim sô ư
đi m c c tri cua ham sô ể ư
L i giaiơ
Cach 1: T đô thi (C) ta suy ra đô thi (C’) cua ư
ham sô (theo phep suy ra đô thi )
Nhin đô thi (C’), ta thây ham sô co 5 điêm c c ư
tri
Cach 2:
+ Ham sô y = f(x) co 2 điêm c c tri ư
+ Ph ng trinh f(x) = 0 co 3 nghiêm đn ươ ơ
+ Ph ng trinh f(x) = 0 co 0 nghiêm bôi le ươ
Vây sô điêm c c tri cua ham sô băng 2 + 3 + 0 ư
= 5
5