Summary of doctoral thesis in materials science: Finite element models in vibration analysis of two-dimensional functionally graded beams

Chia sẻ: Lê Thị Hồng Nhung | Ngày: | Loại File: PDF | Số trang:27

Thêm vào BST

Báo xấu

47
lượt xem 7
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

This thesis aims to develop finite element models for studying vibration of the 2D-FGM beam. These models require high reliability, good convergence speed and be able to evaluate the influence of material parameters, geometric parameters as well as being able to simulate the effect of shear deformation on vibration characteristics and dynamic responses of the 2D-FGM beam.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Summary of doctoral thesis in materials science: Finite element models in vibration analysis of two-dimensional functionally graded beams

MINISTRY OF EDUCATION AND VIETNAM ACADEMY OF TRAINING SCIENCE AND TECHNOLOGY GRADUATE UNIVERSITY SCIENCE AND TECHNOLOGY ----------------------------- TRAN THI THOM FINITE ELEMENT MODELS IN VIBRATION ANALYSIS OF TWO-DIMENSIONAL FUNCTIONALLY GRADED BEAMS Major: Mechanics of Solid code: 9440107 SUMMARY OF DOCTORAL THESIS IN MATERIALS SCIENCE Hanoi – 2019
The thesis has been completed at: Graduate University Science and Technology – Vietnam Academy of Science and Technology. Supervisors: 1. Assoc. Prof. Dr. Nguyen Dinh Kien 2. Assoc. Prof. Dr. Nguyen Xuan Thanh Reviewer 1: Prof. Dr. Hoang Xuan Luong Reviewer 2: Prof. Dr. Pham Chi Vinh Reviewer 3: Assoc. Prof. Dr. Phan Bui Khoi Thesis is defended at Graduate University Science and Technology- Vietnam Academy of Science and Technology at … , on …. Hardcopy of the thesis be found at : - Library of Graduate University Science and Technology - Vietnam national library
1 PREFACE 1. The necessity of the thesis Publications on vibration of the beams are most relevant to FGM beams with material properties varying in one spatial direction only, such as the thickness or longitudinal direction. There are practical circumstances, in which the unidirectional FGMs may not be so appropriate to resist multi-directional variations of thermal and mechanical loadings. Optimiz- ing durability and structural weight by changing the volume fraction of FGM’s component materials in many different spatial directions is a mat- ter of practical significance, being scientifically recognized by the world’s scientists, especially Japanese researchers in recent years. Thus, struc- tural analysis with effective material properties varying in many different directions in general and the vibration of FGM beams with effective mate- rial properties varying in both the thickness and longitudinal directions of beams (2D-FGM beams) in particular, has scientific significance, derived from the actual needs. It should be noted that when the material properties of the 2D-FGM beam vary in longitudinal direction, the coefficients in the differential equation of beam motion are functions of spatial coordinates along the beam axis. Therefore analytical methods are getting difficult to analyze vibration of the 2D-FGM beam. Finite element method (FEM), with many strengths in structural analysis, is the first choice to replace traditional analytical methods in studying this problem. Developing the finite element models, that means setting up the stiffness and mass ma- trices, used in the analysis of vibrations of the 2D-FGM beam is a mat- ter of scientific significance, contributing to promoting the application of FGM materials into practice. From the above analysis, author has selected the topic: Finite element models in vibration analysis of two-dimensional functionally graded beams as the research topic for this thesis. 2. Thesis objective This thesis aims to develop finite element models for studying vibra- tion of the 2D-FGM beam. These models require high reliability, good convergence speed and be able to evaluate the influence of material pa- rameters, geometric parameters as well as being able to simulate the effect of shear deformation on vibration characteristics and dynamic responses of the 2D-FGM beam. 3. Content of the thesis
2 Four main research contents are presented in four chapters of the the- sis. Specifically, Chapter 1 presents an overview of domestic and for- eign studies on the 1D and 2D-FGM beam structures. Chapter 2 pro- poses mathematical model and mechanical characteristics for the 2D- FGM beam. The equations for mathematical modeling are obtained based on two kinds of shear deformation theories, namely the first shear de- formation theory and the improved third-order shear deformation theory. Chapter 3 presents the construction of FEM models based on different beam theories and interpolation functions. Chapter 4 illustrates the nu- merical results obtained from the analysis of specific problems. Chapter 1. OVERVIEW This chapter presents an overview of domestic and foreign regime of re- searches on the analysis of FGM beams. The analytical results are dis- cussed on the basis of two research methods: analytic method and nu- merical method. The analysis of the overview shows that the numerical method in which FEM method is necessary is to replace traditional ana- lytical methods in analyzing 2D-FGM structure in general and vibration of the 2D-FGM beam in particular. Based on the overall evaluation, the thesis has selected the research topic and proposed research issues in de- tails. Chapter 2. GOVERNING EQUATIONS This chapter presents mathematical model and mechanical characteris- tics for the 2D-FGM beam. The basic equations of beams are set up based on two kinds of shear deformation theories, namely the first shear defor- mation theory (FSDT) and the improved third-order shear deformation theory (ITSDT) proposed by Shi [40]. In particular, according to ITSDT, basic equations are built based on two representations, using the cross- sectional rotation θ or the transverse shear rotation γ0 as an independent function. The effect of temperature and the change of the cross-section are also considered in the equations. 2.1. The 2D-FGM beam model The beam is assumed to be formed from four distinct constituent mate- rials, two ceramics (referred to as ceramic1-C1 and ceramic2-C2) and two metals (referred to as metal1-M1 and metal2-M2) whose volume fraction
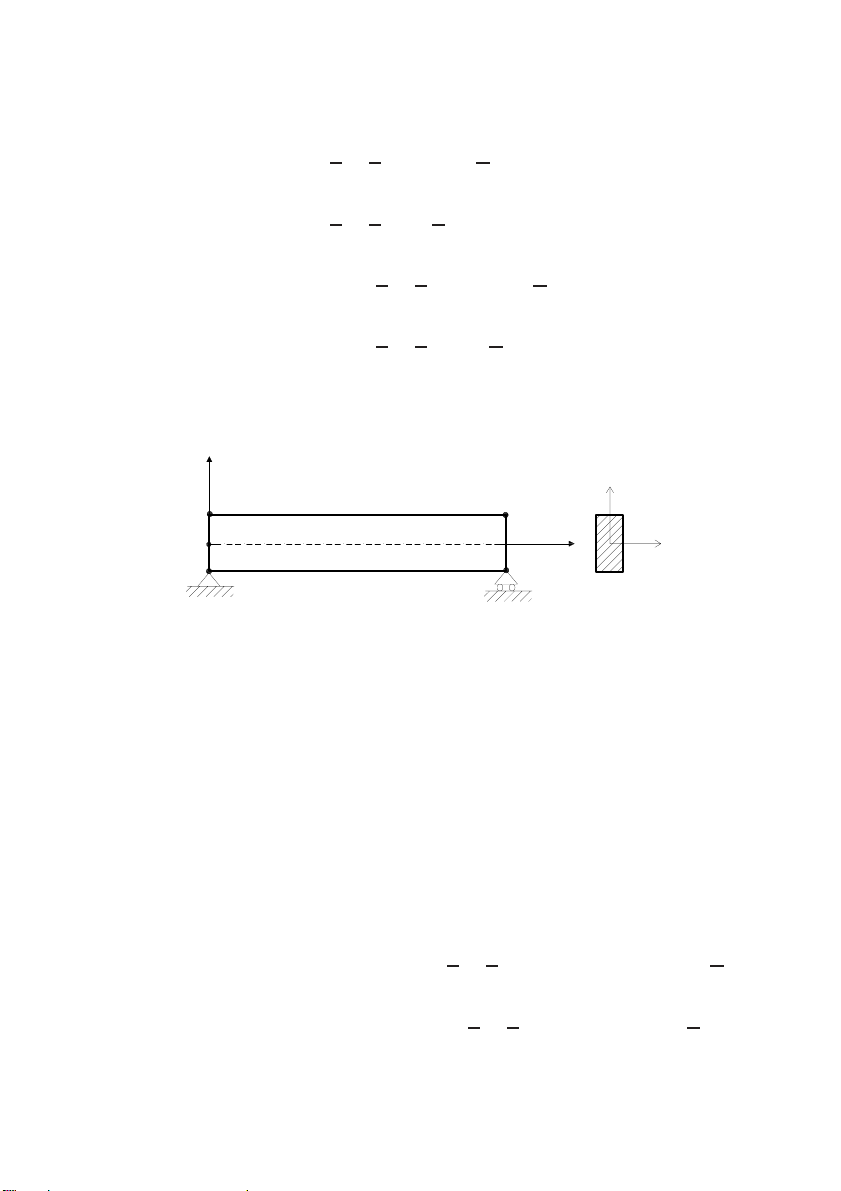
3 varies in both the thickness and longitudinal directions as follows: z 1 nz h x nx i VC1 = + 1− h 2 L nz z 1 x nx VC2 = + h 2 L nz h x nx i (2.1) z 1 VM1 = 1 − + 1− h 2 L nz z 1 x xn VM2 = 1 − + h 2 L Fig. 2.1 illustrates the 2D-FGM beam in Cartesian coordinate system (Oxyz). Z z C1 C2 0 h X y M1 M2 b L, b, h Fig. 2.1. The 2D-FGM beam model In this thesis, the effective material properties P (such as Youngs modulus, shear modulus, mass density, etc.) for the beam are evaluated by the Voigt model as: P = VC1 PC1 +VC2 PC2 +VM1 PM1 +VM2 PM2 (2.2) When the beam is in thermal environment, the effective properties of beams depend not only on the properties of the component materials but also on the ambient temperature. Then, one can write the expression for the effective properties of the beam exactly as follows: h i z 1 nz h x nx i P(x, z, T ) = PC1 (T ) − PM1 (T ) + + PM1 (T ) 1 − h 2 L h i z 1 nz x nx + PC2 (T ) − PM2 (T ) + + PM2 (T ) h 2 L (2.4)
4 For some specific cases, such as nx = 0 or nz = 0, or C1 and C2 are identical, and M1 is the same as M2, the beam model in this thesis re- duces to the 1D-FGM beam model. Thus, author can verification the FEM model of the thesis by comparing with the results of the 1D-FGM beam analysis when there is no numerical result of the 2D-FGM beam. Its important to note that the mass density is considered to be temperature- independent [41]. The properties of constituent materials depend on temperature by a nonlinear function of environment temperature [125]: P = P0 (P−1 T −1 + 1 + P1 T + P2 T 2 + P3 T 3 ) (2.7) This thesis studies the 2D-FGM beam with the width and height are linear changes in beam axis, means tapered beams, with the following three tapered cases [138]: x x Case A : A(x) = A0 1 − c , I(x) = I0 1 − c L L x x 3 Case B : A(x) = A0 1 − c , I(x) = I0 1 − c (2.9) L L x 2 x 4 Case C : A(x) = A0 1 − c , I(x) = I0 1 − c L L 2.2. Beam theories Based on the pros and cons of the theories, this thesis will use Timo- shenko’s first-order shear deformation theory (FSDT) [127] and the im- proved third-order shear deformation theory proposed by Shi (ITSDT) [40] to construct FEM models. 2.3. Equations based on FSDT Obtaining basic equations and energy expressions based on FSDT and ITSDT theory is similar, so Section 2.4 presents in more detail the process of setting up equations based on ITSDT. 2.4. Equations based on ITSDT 2.4.1. Expression equations according to θ From the displacement field, this thesis obtains expressions for strains and stresses of the beam. Then, the conventional elastic strain energy, UB
5 is in the form ZL " 1 UB = A11 εm2 + 2A12 εm εb + A22 εb2 − 2A34 εm εhs − 2A44εb εhs 2 0 (2.27) # 1 1 1 + A66 εhs 2 + 25 B11 − 2 B22 + 4 B44 γ02 dx 16 2h h where A11 , A12 , A22 , A34 , A44 , A66 and B11 , B22 , B44 are rigidities of beam and defined as: Z (A11 , A12 , A22 , A34 , A44 , A66 )(x, T ) = E(x, z, T )(1, z, z2 , z3 , z4 , z6 )dA A(x) Z (B11 , B22 , B44 )(x, T ) = G(x, z, T )(1, z2 , z4 )dA A(x) (2.28) The kinetic energy of the beam is as follow: ZL " 1 1 1 T = I11 (u˙20 + w˙ 20 ) + I12 u˙0 (w˙ 0,x + 5θ˙ ) + I22 (w˙ 0,x + 5θ˙ )2 2 2 16 0 # 10 5 25 − 2 I34 u˙0 (w˙ 0,x + θ˙ ) − 2 I44 (w˙ 0 + θ˙ )(w˙ 0 + 5θ˙ ) + 4 I66 (w˙ 0,x + θ˙ )2 dx 3h 6h 9h (2.29) in which Z (I11 , I12 , I22 , I34 , I44 , I66 )(x) = ρ (x, z) 1, z, z2 , z3 , z4 , z6 dA (2.30) A(x) are mass moments. The beam rigidities and mass moments of the beam are in the follow- ing forms: x nx Ai j = AC1M1 ij − A C1M1 ij − A C2M2 ij L x nx (2.31) C1M1 C1M1 C2M2 Bi j = Bi j − Bi j − Bi j L
6 with AC1M1 ij , BC1M1 ij are the rigidities of 1D-FGM beam composed of C1 C2M2 and M1; Ai j , Bi j C2M2 are the rigidities of 1D-FGM beam composed of C2 and M2. Noting that rigidities of 1D-FGM beam are functions of z only, the explicit expressions for this rigidities can easily be obtained. 2.4.2. Expression equations according to γ0 Using a notation for the transverse shear rotation (also known as clas- sic shear rotation), γ0 = w0,x + θ as an independent function, the axial and transverse displacements in (2.13) can be rewritten in the following form 1 5 u(x, z,t) = u0 (x,t) + z 5γ0 − 4w0,x − 2 z3 γ0 4 3h (2.35) w(x, z,t) = w0 (x,t) Similar to the construction of basic equations according to θ , the thesis also receives basic equations expressed in γ0 . 2.5. Initial thermal stress Assuming the beam is free stress at the reference temperature T0 and it is subjected to thermal stress due to the temperature change. The initial thermal stress resulted from a temperature ∆T is given by [18, 70]: σxx T = −E(x, z, T )α (x, z, T )∆T (2.41) in which elastic modulus E(x, z, T ) and thermal expansion α (x, z, T ) are obtained from Eq.(2.4). The strain energy caused by the initial thermal stress σxx T has the form [18, 65]: ZL 1 UT = NT w20,x dx (2.42) 2 0 where NT is the axial force resultant due to the initial thermal stress. σxx T: Z Z NT = σxx T dA = − E(x, z, T )α (x, z, T )∆T dA (2.43) A(x) A(x) The total strain energy resulted from conventional elastic strain energy UB , and strain energy due to initial thermal stress UT [70]. 2.6. Potential of external load
7 The external load considered in the present thesis is a single moving constant force with uniform velocity. The force is assumed to cause bend- ing only for beams. The potential of this moving force can be written in the following form h i V = −Pw0 (x,t)δ x − s(t) (2.44) where δ (.) is delta Dirac function; x is the abscissa measured from the left end of the beam to the position of the load P, t is current time calcu- lated from the time when the load P enters the beam, and s(t) = vt is the distance which the load P can travel. 2.7. Equations of motion In this section, author presents the equations of motion based on ITSDT with γ0 being the independent function. Motion equations for beams based on FSDT and ITSDT with θ is independent function that can be obtained in the same way. Applying Hamiltons principle, one obtained the motion equations system for the 2D-FGM beam placed in the temper- ature environment under a moving force as follows: " 1 5 I11 u¨0 + 5γ¨0 −4w¨ 0,x I12 − 2 I34 γ¨0 − A11 u0,x 4 3h # (2.51) 1 5 + A12 5γ0,x − 4w0,xx − 2 A34 γ0,x = 0 4 3h ,x " # " 1 5 5γ¨0 − 4w¨ 0,x I22 − 2 I44 γ¨0 − A12 u0,x I11 w¨ 0 + I12 u¨0 + 4 3h ,x # 1 5 h i + A22 5γ0,x − 4w0,xx − 2 A44 γ0,x = NT w0,x − Pδ x − s(t) 4 3h ,x ,xx (2.52)
8 1 1 1 1 5 I12 u¨0 + I22 5γ¨0 − 4w¨ 0,x − 2 I34 u¨0 − 2 I44 γ¨0 − w¨ 0,x 4 16 " 3h 3h 2 5 1 1 1 + 4 I66 γ¨0 − A12 u0,x + A22 5γ0,x − 4w0,xx − 2 A34 u0,x 9h 4 16 3h # 1 5 5 1 1 1 − 2 A44 γ0,x − w0,xx − 4 A66 γ0,x + 5 B11 − 2 B22 + 4 B44 γ0 = 0 3h 2 9h 16 2h h ,x (2.53) Notice that the coefficients in the system of differential equations of motion are the rigidities and mass moments of the beam, which are the functions of the spatial variable according to the length of the beam and the temperature, thus solving this system using analytic method is diffi- cult. FEM was selected in this thesis to investigate the vibration charac- teristics of beams. Conclusion of Chapter 2 Chapter 2 has established basic equations for the 2D-FGM beam based on two kinds of shear deformation theories, namely FSDT and ITSDT. The effect of temperature and the change of the cross-section is consid- ered in establishing the basic equations. Energy expressions are presented in detail for both FSDT and ITSDT in Chapter 2. In particular, with ITSDT, basic equations and energy expressions are established on the cross-sectional rotation θ or the transverse shear rotation γ0 as indepen- dent functions. The expression for the strain energy due to the tempera- ture rise and the potential energy expression of the moving force are also mentioned in this Chapter. Equations of motion for the 2D-FGM beam are also presented using ITSDT with γ0 as independent function. These energy expressions are used to obtain the stiffness matrices and mass ma- trices used in the vibration analysis of the 2D-FGM beam in Chapter 3. Chapter 3. FINITE ELEMENT MODELS This chapter builds finite element (FE) models, means that establish expressions for stiffness matrices and mass matrices for a characteristic element of the 2D-FGM beam. The FE model is constructed from the energy expressions received by using the two beam theories in Chapter 2. Different shape functions are selected appropriately so that beam ele- ments get high reliability and good convergence speed. Nodal load vector
9 and numerical procedure used in vibration analysis of the 2D-FGM beam are mentioned at the end of the chapter. 3.1. Model of finite element beams based on FSDT This model constructed from Kosmatka polynomials referred as FBKo in this thesis can be avoided the shear-locking problem. In addition, this model has a high convergence speed and reliability in calculating the nat- ural frequencies of the beam. However, the FBKo model with 6 d.o.f has the disadvantage that the Kosmatka polynomials must recalculate each time the element mesh changes, thus time-consuming calculations. The FE model uses hierarchical functions, referred as FBHi model in the the- sis, which is one of the options to overcome the above disadvantages. Recently, hierarchical functions are used to develop the FEM model in 1D-FGM beam analysis (such as Bui Van Tuyen’s thesis). Based on the energy expressions received in Chapter 2, the thesis has built FBKo model and FBHi model using the Kosmatka function and hierarchical interpola- tion functions, respectively. The process of building FE models is similar, Section 3.2 will presents in detail the construction of stiffness and mass matrices for a characteristic element based on ITSDT. 3.2. Model of finite element beams based on ITSDT With two representations of the displacement field, two FEM models corresponding to these two representations will be constructed below. For convenience, in the thesis, FEM model uses the cross-sectional rotation θ as the independent function is called TBSθ model, FEM model uses the transverse shear rotation as the independent function is called TBSγ . 3.2.1. TBSθ model Different from the FE model based on FSDT, the vector of nodal dis- placements for two-node beam element (i, j), using the high order shear deformation theory in general and ITSDT in particular, has eight compo- nents: dSθ = {ui wi wi,x θi u j w j w j,x θ j }T (3.28) The displacements u0 , w0 and rotation θ are interpolated from the nodal displacements as u 0 = Nu d S θ , w 0 = Nw d S θ , θ = Nθ d S θ (3.29) where Nu , Nw and Nθ are, respectively, the matrices of shape functions
10 for u0 , w0 and θ . Herein, linear shape functions are used for the axial displacement u0 (x,t) and the cross-section rotation θ (x,t), Hermite shape functions are employed for the transverse displacement w0 (x,t). With the interpolation scheme, one can write the expression for the de- formation components in the form of a matrix through a nodal displace- ments vector (3.28) as follows εmSθ = u0,x = Bm Sθ Sθ d 1 εbSθ = (5θ,x + w0,xx ) = BSbθ dSθ 4 (3.33) Sθ 5 Sθ Sθ εhs = 2 (θ,x + w0,xx ) = Bhs d 3h εsSθ = θ + w0,x = Bm Sθ Sθ d In (3.33), the strain-displacement matrices BSmθ , BSbθ , Bhs Sθ and BSs θ are as follows n 1 1 BSmθ = − o 0 0 0 0 0 0 l l 1 6 12x 4 6x 5 6 12x 2 6x 5 o BSbθ = n 0 − 2+ 3 − + 2 − 0 2− 3 − + 2 4 l l l l l l l l l l Sθ 5 n 6 12x 4 6x 1 6 12x 2 6x 1 o Bhs = 2 0 − 2 + 3 − + 2 − 0 2− 3 − + 2 3h l l l l l l l l l l 6x 6x 2 4x 3x l − x2 6x 6x 2 2x 3x x o 2 BSs θ = 0 − 2 + 3 1 − + 2 n 0 2 − 3 − + 2 l l l l l l l l l l (3.34) The elastic strain energy of the beam UB in Eq.(2.27) can be written in the form 1 nE UB = ∑(dSθ )T kSθ dSθ (3.9) 2 where the element stiffness matrix kSθ is defined as kSθ = kSmθ + kbSθ + ksSθ + khs Sθ + kSc θ (3.35)
11 in which Zl T Zl T kSmθ = Sθ Bm Sθ A11 Bm dx ; kSbθ = BSbθ A22 BSbθ dx 0 0 Zl T 1 1 1 kSs θ = 25 BSs θ B11 − 2 B22 + 4 B44 BSs θ dx 16 2h h 0 Zl T Sθ Sθ Sθ khs = Bhs A66 Bhs dx 0 Zl " # T T T kSc θ = BSmθ A12 BSbθ − Bm Sθ A34 BShsθ − BbSθ A44 BShsθ dx 0 (3.36) One write the kinetic energy in the following form 1 nE ˙ K T ˙ K 2∑ (d ) m d T = (3.13) in which the element consistent mass matrix is in the form m = m11 12 22 34 44 66 11 uu + muθ + mθ θ + muγ + mθ γ + mγγ + mww (3.37) with Zl Zl 1 m11 uu = NTu I11 Nu dx ; m12 uθ = NTu I12 (Nw,x + 5Nθ )dx 4 0 0 Zl Zl 1 T 5 m22 θθ = (Nw,x + 5NθT )I22 (Nw,x + 5Nθ )dx ; m34 uγ = − NTu I34 (Nw,x + Nθ )dx 16 3h2 0 0 Zl 5 mθ44γ = − (NTw,x + 5NTθ )I44 (Nw,x + Nθ )dx 12h2 0 Zl Zl 25 m66 γγ = 4 (NTw,x + NθT )I66 (Nw,x + Nθ )dx ; m11 ww = NTw I11 Nw dx 9h 0 0 (3.38) are the element mass matrices components.
12 3.2.2. TBSγ model With γ0 is the independent function, the vector of nodal displacements for a generic element, (i, j), has eight components: dSγ = {ui wi wi,x γi u j w j w j,x γ j }T (3.39) The axial displacement, transverse displacement and transverse shear rotation are interpolated from the nodal displacements according to u0 = Nu dSγ , w0 = Nw dSγ , γ0 = Nγ dSγ (3.40) with Nu , Nw and Nγ are the matrices of shape functions for u0 , w0 and γ0 , respectively. Herein, linear shape functions are used for the axial displacement u0 (x,t) and the transverse shear rotation γ0 , Hermite shape functions are employed for the transverse displacement w0 (x,t). The con- struction of element stiffness and mass matrices are completely similar to TBSθ model. 3.3. Element stiffness matrix due to initial thermal stress Using the interpolation functions for transverse displacement w0 (x,t), one can write expressions for the strain energy due to the temperature rise (2.42) in the matrix form as follows 1 nE T 2∑ UT = d kT d (3.44) where Zl kT = BtT NT Bt dx (3.45) 0 is the stiffness due to temperature rise. For different beam theories, the element stiffness matrix due to temperature rise has the same form (3.45). The only difference is that the difference of the shape functions Nw is chosen for w0 (x,t) leading to the difference of the strain-displacement matrix Bt = (Nw ),x in (3.45). 3.4. Discretized equations of motion Ignoring damping effect of the beam, the equations of motion for 2D- FGM beam can be written in the context of the finite element analysis as MD ¨ + KD = Fex (3.49)
13 in which D, D ¨ are, respectively, the vectors of structural nodal displace- ments and accelerations, K, M, Fex are the stiffness matrices due to the beam deformation and temperature rise, the mass matrix and the nodal load vector of the structure, respectively. In the free vibration analysis, the right-hand side of (3.49) is set to zero 0: MD ¨ + KD = 0 (3.52) 3.5. Numerical procedure Solving the equation (3.52) is brought about solving the eigenvalue problem. Eq (3.49) can be solved by the direct integration Newmark method. The constant average acceleration method which ensures the unconditional stability is employed in this thesis. Conclusion of Chapter 3 Chapter 3 builds FE model for a two-node element based on two kinds of shear deformation theories for beams. Based on FSDT, FE models are constructed by using two different shape functions, such as the Kosmatka function and hierarchical shape functions. Based on ITSDT, FE models are constructed by linear and Hermite shape functions. The expression for stiffness and mass matrix for the models based on ITSDT is built on the basis of considering the cross-section rotation or transverse shear rotation as independent functions. The expression for the stiffness matrix due to temperature rise and the vector of nodal force is also built into Chapter. Chapter 4. NUMERICAL RESULTS AND DISCUSSION The numerical results are presented on the basis of analyzing three problems: (1) Free vibration analysis of the 2D-FGM beam in thermal environment; (2) Free vibration analysis of the tapered 2D-FGM beam; (3) Forced vibration analysis of the 2D-FGM beam excited by a moving force. From the numerical results obtained, some conclusions relate to the influence of the material parameter, the taper ratio, aspect ratio and temperature rise on the fundamental frequency and the vibration mode to be extracted. Dynamic behaviour of 2D-FDM beams under the action of moving force are also discussed in Chapter. 4.1. Validation and convergence of FE models 4.1.1. Convergence of FE models
14 The convergence of four FE models developed in the thesis in evalu- ating the fundamental frequency parameter µ of a simply supported 2D- FGM beams with constant cross-section (c = 0) is examined in the thesis. The effect of temperature is not considered herein (∆T = 0K). Some com- ments can be drawn as follows: - The fundamental frequency parameters of 2D-FGM beams received from four FE models developed in the thesis are very close. - Three of the four FE models have high convergence rate, namely FBKo model, FBHi model and TBSγ model. When using these three models to calculate, the fundamental frequency parameters of the 2D- FGM beam converges to the same value with only 16 or 18 elements. However, TBSθ model converges very slowly, requiring up to 70 ele- ments. - Values of the grading indexes pairs (nx , nz ) do not affect to the con- vergence rate of the FE models. From the convergence of the above-mentioned FE models, the thesis will only use models with good convergence to calculate and compare nu- merical results. The convergence of FBHi model in evaluating the funda- mental frequency parameter of the tapered 2D-FGM beam is also carried out by the thesis. In calculating the fundamental frequency parameter, convergence rate of FBHi model of the tapered 2D-FGM beam is slower than a constant cross-section ones. It requires up to 30 elements to achieve the convergence rate. 4.1.2. Validation of FE models Since there is no data on the vibration of the 2D-FGM beam with the power-law variations of the material properties as considered in the the- sis, the comparison will be carried out for the 1D-FGM beam, a special case of the 2D-FGM beam. The fundamental frequency parameter and the dynamic response obtained in the thesis are compared with the data available in the literature. The effect of temperature and change of the cross-section are considered. Comparative results show that the FE mod- els developed in the thesis are reliable and it can be used to study vibration of the 2D-FGM beam. 4.2. Free Vibration 4.2.1. Constant cross-section beams 4.2.1.1. Influence of material distribution
15 Fig. 4.1 illustrates the influence of grading indexes on the first four natural frequency parameters of S-S beams with ∆T = 50K 5 20 4 µ1 15 µ2 3 2 10 2 2 1.5 2 1.5 2 1 1.5 1 1.5 n 0.5 1 1 x 0.5 n n 0.5 0.5 n 0 0 z x 0 0 z 40 60 50 30 µ3 µ4 40 20 30 2 2 1.5 2 1.5 2 1 1.5 1 1.5 nx 0.5 1 0.5 1 0.5 nz n 0.5 n 0 0 x 0 0 z Fig. 4.1. Influence of grading indexes on the first four natural frequency parameters of S-S beams with ∆T = 50K From Fig. 4.1 ones can see that: - At a given value of the index nx , the fundamental frequency param- eter µ1 tends to decreased by the increase in the index nz . The decrease of µ1 is more significant for the beam with a higher index nx . The effect of the index nx on the fundamental frequency parameter is different from that of the index nz , and µ1 increases with the increase of the nx index. However, the increase of µ1 is more significant for the beam associated with a lower index nz . - The fundamental frequency parameter attains a maximum value at nx = 2 and nz = 0, and this is the special case when the beam degrades to the axially FG beam made of the two ceramics. - At the given value of the temperature rise, the effect of the grading indexes on the higher frequency parameters is similar to the case of the fundamental frequency parameter, they are also decreased by increasing the index nz and they are increased by increasing index nx . 4.2.1.2. Influence of temperature rise Fig. 4.2 illustrates the influence of grading indexes on the fundamental frequency parameters of S-S beams for various temperature rise ∆T . Some comments can be drawn from Fig. 4.2 as follows:
16 5 5 4 4 µ1 1 µ 3 3 2 2 2 2 1.5 2 1.5 2 1 1.5 1 1.5 nx 0.5 1 nx 0.5 1 0.5 nz 0.5 n 0 0 0 0 z (a) ∆T=0 K (a) ∆T=20 K 5 5 4 4 µ1 µ1 3 3 2 2 2 1.5 2 2 1 1.5 1.5 2 n 0.5 1 1 1.5 x 0 0 0.5 nz 0.5 1 n 0.5 n x 0 0 z (c) ∆T=40 K (d) ∆T=80 K Fig. 4.2. Influence of grading indexes on µ1 of S-S beams for various temperature rise ∆T - The relation between the grading indexes and frequency parameters unchanged when the value of ∆T increases. That means, the frequency parameters decrease when increasing the index nz and they increased with increasing the index nx . However, this relation is affected by the temper- ature rise. In particular, when nz increases from 0 to 2, the fundamen- tal frequency parameters of the beam is significantly decrease, especially when the index nx is large. - The fundamental frequency parameters of beams is significantly de- crease when the value of the ∆T increases. 4.2.1.3. Influence of the boundary conditions Some comments can be drawn from this section as follows: - The frequency parameters of the C-C beam is highest while that one of C-F beams is lowest. At the reference temperature (∆T = 0K), the variation of the frequency parameters with the grading indexes of the C-C beam and the C-F beam is similar to that of the S-S beam. However, the C-F beam is more sensitive to the change in the index nx than the S-S and C-C beams, especially when nz is small.
17 - The effect of the grading indexes on the higher frequency parameters of the C-C beam and the C-F beam is similar to that of the S-S beam. - The variation of the frequency parameters of C-C and C-F beams with values of the temperature rise are similar to S-S beams. However, this variation is strongly influenced by boundary conditions. Specifically, C-C beams are less affected by temperature rise. In contrast, C-F beams are very sensitive to the rise of temperature. 4.2.1.4. Influence of the aspect ratio The effect of the beam aspect ratio, L/h, on the fundamental frequency parameters of the beam is illustrated in Fig. 4.7, where the variations of the fundamental frequency parameter with the grading indexes of the S- S beam are depicted for two values of the aspect ratio, L/h = 10 and L/h = 30, and for a temperature rise ∆T = 50K. In Fig. 4.7, the relation between the grading indexes and frequency pa- rameters unchanged when the value of L/h increases, means an increase in the aspect ratio leads to a significantly decrease of the fundamental fre- quency parameter. It should be noted that previous studies have shown that when beams are placed at reference temperature, an increase in the aspect ratio leads to a significantly increase of the fundamental frequency parameter. However, as shown in Fig. 4.7, this is no longer true when the effect of temperature is considered. This can be explained by the fact that when beams are placed in temperature environments, the stiffness of the beams with high aspect ratio is significantly decrease than that of beams with low aspect ratio . 4.5 4.5 4 4 3.5 3.5 3 1 3 µ µ1 2.5 2.5 2 2 1.5 1.5 2 2 1.5 2 1.5 2 1 1.5 1 1.5 nx 1 n 0.5 1 0.5 0.5 n x 0.5 nz z 0 0 0 0 (a) ∆T=50 K, L/h=10 (b) ∆T=50 K, L/h=30 Fig. 4.7. Variation of fundamental frequency parameter with grading indexes of S-S beam in thermal environment with different values of aspect ratio
18 4.2.1.5. Mode shapes Fig. 4.8 illustrates the first three mode shapes for u0 , w0 and γ0 of S- S beams with two pairs of the grading indexes: (nx , nz ) = (0.0, 0.5) and (nx , nz ) = (0.5, 0.5), in the reference temperature (∆T = 0). 1.5 1.5 mode 1 w mode 1 0 1 u 1 0 γ0 0.5 0.5 0 0 n =0, n =0.5 n =0.5, n =0.5 x z x z −0.5 −0.5 0 0.25 0.5 0.75 1 0 0.25 0.5 0.75 1 1.5 1.5 mode 2 mode 2 1 1 0.5 0.5 0 0 −0.5 −0.5 −1 −1 −1.5 −1.5 0 0.25 0.5 0.75 1 0 0.25 0.5 0.75 1 1.5 1.5 mode 3 mode 3 1 1 0.5 0.5 0 0 −0.5 −0.5 −1 −1 −1.5 −1.5 0 0.25 0.5 0.75 1 0 0.25 0.5 0.75 1 (a) (b) Fig. 4.8. The first three mode shapes for u0 , w0 and γ0 of S-S beams with ∆T = 0K: (a) (nx , nz ) = (0, 0.5), (b) (nx , nz ) = (0.5, 0.5) As can be seen from the figure, the mode shapes of the 2-D FGM beam as depicted in Fig. 4.8(b) are very different from that of the unidirectional transverse FGM beam as depicted in Fig. 4.8(a). While the first and third modes of the transverse displacement w0 of 1D-FGM beam are symmetric with respect to the mid-span, that of the 2D FGM beam are not. The figure also shows the difference in the mode shape of u0 and γ0 of the 2-D FGM beam with that of the 1D beam, and the asymmetric of the second mode for γ0 with respect to the mid-span is clearly seen from Fig. 4.8(b). Thus, the variation of the constituent materials in the longitudinal directions has a significant influence on the vibration modes of the beam. The mode shapes for u0 , w0 and γ0 of the S-S 2D-FGM beam in thermal environment are also considered for various values of the grading indexes. The grading indexes and temperature rise have a significant influence on the vibration modes of the beam, and not only vibration amplitude but also the position of the critical point is changed. 4.2.2. Tapered beams