Gi i thi uớ ệ
Đ tăng hàmộ
Big-O
Tính ch tấ
Big-Theta
Tính ch tấ
Little-o
Đ ph c t p ộ ứ ạ
X u nh tấ ấ
Trung bình
Tính đúng đ nắ
Đi u ki nề ệ
L pặ
Ví dụ
Tóm t tắ
1/35T toán đ i h c FPTổ ạ ọ
13/12/12
Ch ng 2.2, 2.3 Kenneth H. Rosenươ
Xuân 2008
Đ i h c FPT ạ ọ
Discrete Mathematics I
đ ph c t p & tính ộ ứ ạ
đúng đ n ắ
complexity & correctness
đ ph c t p & tính ộ ứ ạ
đúng đ n ắ
complexity & correctness
Thu t toán ậ
Algorithm
Thu t toán ậ
Algorithm

Gi i thi uớ ệ
Đ tăng hàmộ
Big-O
Tính ch tấ
Big-Theta
Tính ch tấ
Little-o
Đ ph c t p ộ ứ ạ
X u nh tấ ấ
Trung bình
Tính đúng đ nắ
Đi u ki nề ệ
L pặ
Ví dụ
Tóm t tắ
2/35T toán đ i h c FPTổ ạ ọ
13/12/12
Thu t toánậ GI I THI U Ớ Ệ
Algorithm
INTRODUCTION
Gi i thi uớ ệ
Chúng ta s h c:ẽ ọ
•Đánh giá v đ tăng c a hàmề ộ ủ
•Big-O, big-Theta
•Đ ph c t p thu t toán: Đ ph c t p th i gianộ ứ ạ ậ ộ ứ ạ ờ
•Tr ng h p x u nh tườ ợ ấ ấ
•Tr ng h p trung bìnhườ ợ
•Tính đúng đ n thu t toánắ ậ
Gi i thi uớ ệ
Đ tăng hàmộ
Big-O
Tính ch tấ
Big-Theta
Tính ch tấ
Little-o
Đ ph c t p ộ ứ ạ
X u nh tấ ấ
Trung bình
Tính đúng đ nắ
Đi u ki nề ệ
L pặ
Ví dụ
Tóm t tắ
3/35T toán đ i h c FPTổ ạ ọ
13/12/12
Thu t toánậ BIG-O
Algorithm BIG-O
Đ nh nghĩaị Definition
Đ nh nghĩaị Definition
Cho f(x) và g(x) là hai hàm s t t p các s nguyên ố ừ ậ ố
ho c s th c đ n t p các s th c. Ta nói ặ ố ự ế ậ ố ự f(x) là O(g(x))
ho c ặf(x) là big-O c a ủg(x) hay f(x) ∈ O(g(x)) n u t n t i ế ồ ạ
hai h ng s ằ ố C và k sao cho
|f(x)| ≤ C|g(x)| v i m i ớ ọ x ≥ k.
Cho f(x) và g(x) là hai hàm s t t p các s nguyên ố ừ ậ ố
ho c s th c đ n t p các s th c. Ta nói ặ ố ự ế ậ ố ự f(x) là O(g(x))
ho c ặf(x) là big-O c a ủg(x) hay f(x) ∈ O(g(x)) n u t n t i ế ồ ạ
hai h ng s ằ ố C và k sao cho
|f(x)| ≤ C|g(x)| v i m i ớ ọ x ≥ k.
Big-O
V i m i thu t toán s phép toán c n th c hi n s là m t ớ ỗ ậ ố ầ ự ệ ẽ ộ
hàm s theo kích th c đ u vào. Chúng ta s đánh giá ố ướ ầ ẽ
tính hi u qu c a m i thu t toán b ng cách kh o sát đ ệ ả ủ ỗ ậ ằ ả ộ
tăng c a hàm này. ủ
Ta s ch xét các hàm d ng nên s b d u | |ẽ ỉ ươ ẽ ỏ ấ
Gi i thi uớ ệ
Đ tăng hàmộ
Big-O
Tính ch tấ
Big-Theta
Tính ch tấ
Little-o
Đ ph c t p ộ ứ ạ
X u nh tấ ấ
Trung bình
Tính đúng đ nắ
Đi u ki nề ệ
L pặ
Ví dụ
Tóm t tắ
4/35T toán đ i h c FPTổ ạ ọ
13/12/12
Thu t toánậ BIG-O
Algorithm BIG-O
Ví dụ Example
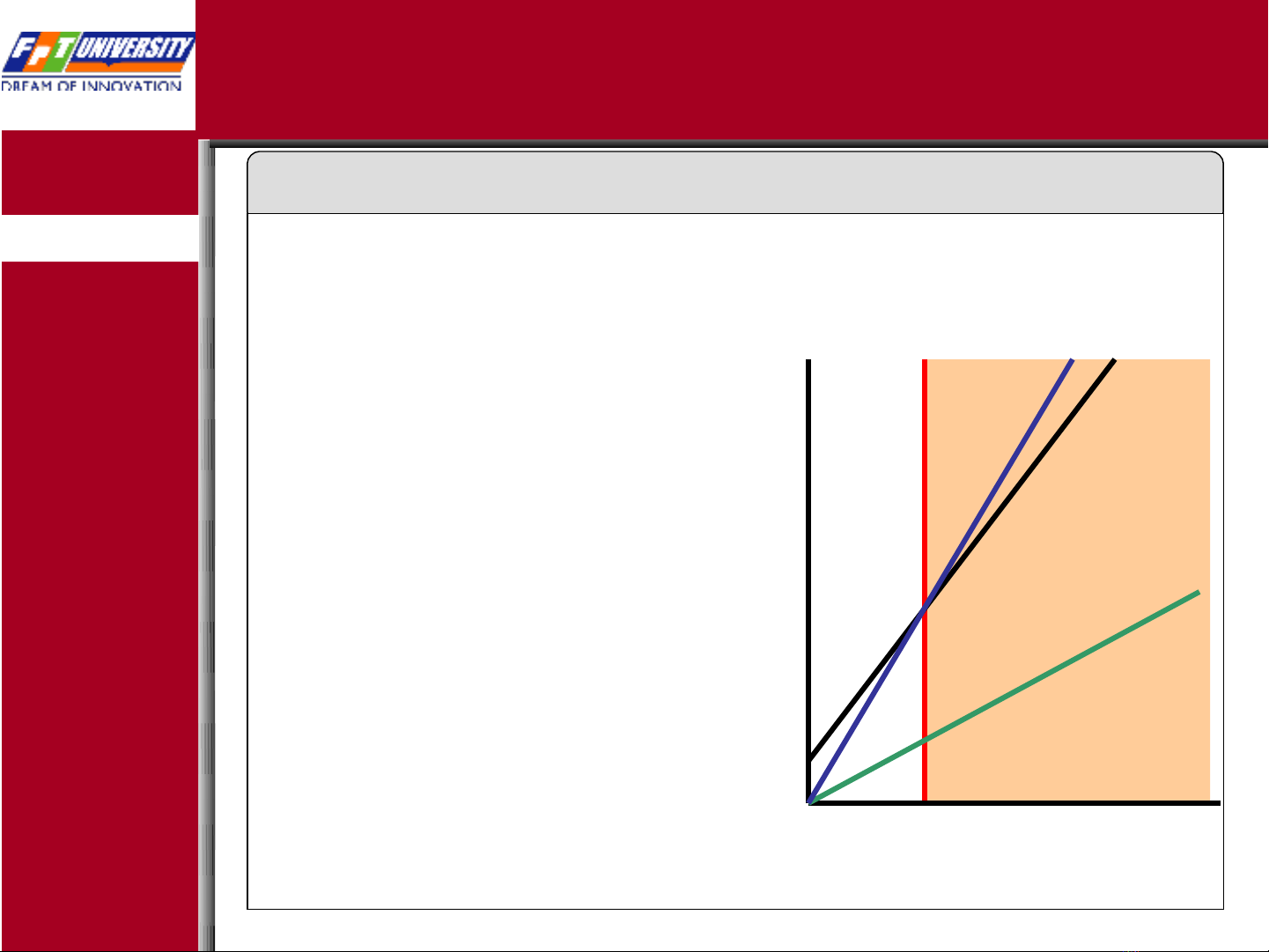
Ch ng minh ứf(n) = 30n + 8 là big-O c a ủg(n) = n.
Ta c n ch ng minh ầ ứ ∃c,k: ∀n > k: 30n + 8 ≤ cn.
L y ấc = 31, k = 8. Khi đó
v iớ n > k = 8,
cn = 31n = 30n + n > 30n+8
n>k=8 →
n
30n+8
cn =
31n
30n+8 ∈O(n)
Giá tr c th c a ị ụ ể ủ c và k
g i là ọb ng ch ngằ ứ . Ta có
th tìm nhi u b ng ch ng. ể ề ằ ứ
Ch ng h n:ẳ ạ
c = 32, k = 9
Big-O
Gi i thi uớ ệ
Đ tăng hàmộ
Big-O
Tính ch tấ
Big-Theta
Tính ch tấ
Little-o
Đ ph c t p ộ ứ ạ
X u nh tấ ấ
Trung bình
Tính đúng đ nắ
Đi u ki nề ệ
L pặ
Ví dụ
Tóm t tắ
5/35T toán đ i h c FPTổ ạ ọ
13/12/12
giai th a ừ
Thu t toánậ BIG-O
Algorithm BIG-O
Khái ni m big-ệO đ c s d ng đ đánh giá s phép toán ượ ử ụ ể ố
c n dùng đ gi i m t bài toán theo m t th t c ho c m t ầ ể ả ộ ộ ủ ụ ặ ộ
thu t toán c th . Các hàm s c b n th ng đ c dùng ậ ụ ể ố ơ ả ườ ượ
đ so sánh là: ể
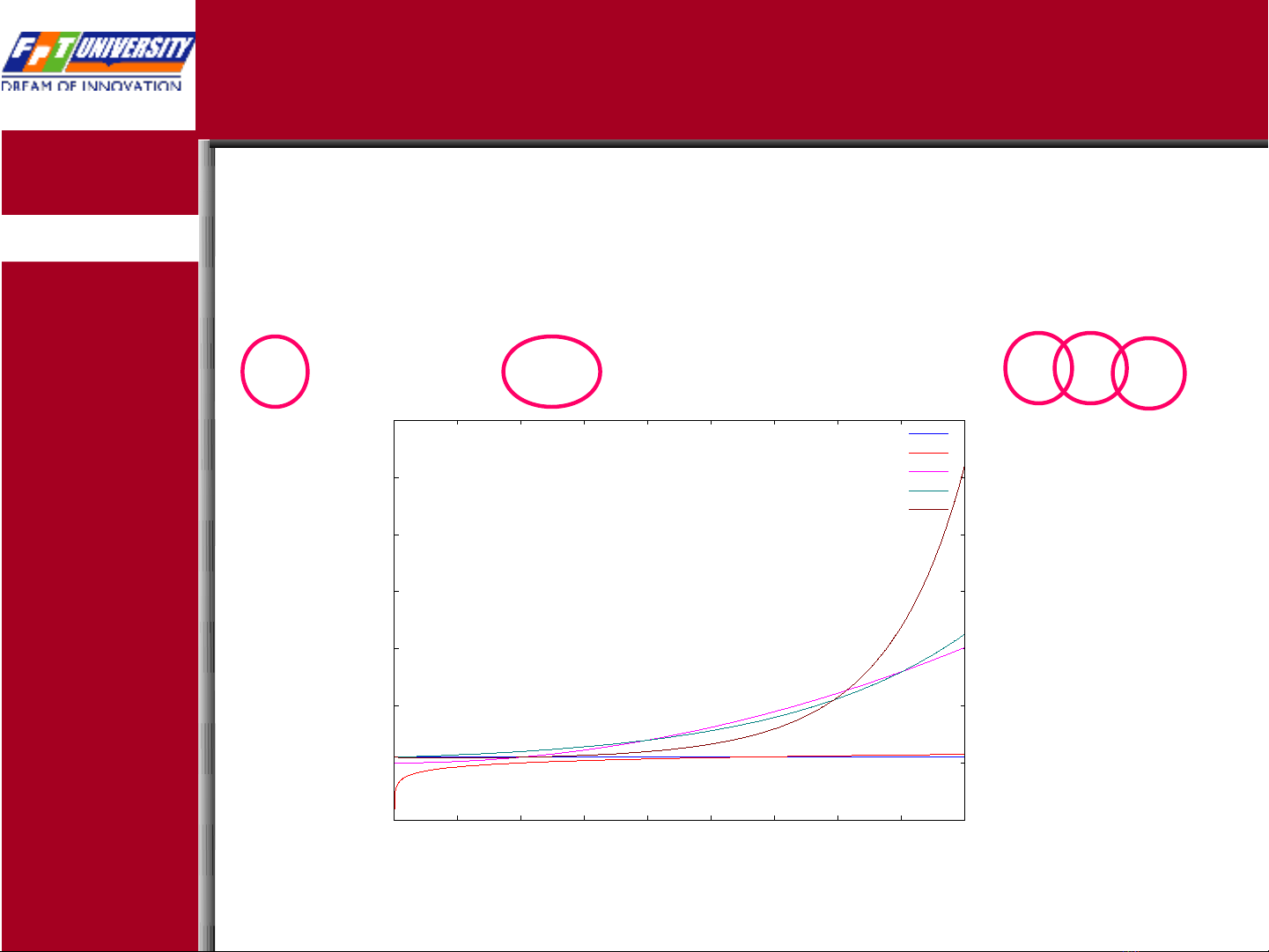
1, log(log(n)), log(n), logk(n), n1/k, n, nlog(n), nk, an, n!, nn
h ng ằlogarit đa th c ứ
mũ
-10
0
10
20
30
40
50
60
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
n
1
log(n)
n^2
2^n
n!
Big-O


























