Trường THPT chuyên ĐỀ THI THỬ ĐẠI HỌC ĐỢT 1
NGUYỄN QUANG DIÊU Môn: Toán khối D
Thời gian làm bài: 180 phút (Không kể thời gian phát đề)
I/ PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)
Câu 1/ (2,0 điểm). Cho hàm số
1
3
x
x
y có đồ thị là (C)
a/ Khảo sát sự biến thiên và vẽ đồ thị hàm số đã cho
b/ Tìm tọa độ điểm M trên (C) sao cho độ dài IM là ngắn nhất
(I: giao điểm hai tiệm cận của(C))
Câu 2/ (1 điểm).Giải phương trình: 3
1
2
sin
2
cos
2
4sin2cos
2
x
x
xx
Câu 3/ Giải hệ phương trình:
021
01
2
2
yyxx
yxyx
Câu 4/ ( 1 điểm). Tính:
dxxxxA 2sin1lncossin
4
0
Câu 5/ ( 1 điểm). Cho lăng trụ đứng ABC.A/B/C/ có (A/BC) tạo với đáy góc 600, tam giác
A/BC có diện tích bằng 38
a/Gọi M ,N lần lượt là trung điểm của BB/ và CC/. Tính thể tích khối tứ diện A/AMN
b/ Tính khoảng cách giữa hai cạnh A/B và AC
Câu 6/ ( 1 điểm) . Gọi 1
x,2
x , 3
x là nghiệm phương trình:
07329232 2223 mmxmmxmx
Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức: 321
2
3
2
2
2
1xxxxxxA
II . PHẦN RIÊNG(3,0 điểm): Thí sinh chỉ được làm một trong hai phần (phần A hoặc phần B)
A . Theo chương trình chuẩn
Câu 7.a (1,0 điểm). Cho tam giác ABC với B(1;–2),phương trình đường cao vẽ từ A là
d: x –y + 3 = 0.Tìm tọa độ A ,C của tam giác.Biết C thuộc đường thẳng : 2x + y –1 = 0 và
diện tích tam giác ABC bằng 1
Câu 8.a (1,0 điểm).Cho A(5 ; 3 ; – 4) và B(1; 3 ; 4). Tìm tọa độ điểm C thuộc mặt phẳng
(Oxy) sao cho tam giác ABC cân đỉnh C và có diện tích 58S.
Câu 9 .a (1,0 điểm ).Giải phương trình: 36213362 222 263 xxxxxx
B . Theo chương trình nâng cao
Câu 7.b (1,0 điểm). Cho hai đường tròn (C1): x2 + y2 = 13 và (C2): (x –6)2 + y2 = 25 cắt nhau
tại A. Viết phương trình đường thẳng qua A (2 ; 3) cắt (C1) và (C2) thành hai dây cung bằng
nhau
Câu 8.b (1,0 điểm). Cho hai đường thẳng lần lượt có phương trình
1
9
2
4
1
7
:
1
zyx
d
và
3
1
2
1
7
3
:
2
zyx
d. Lập phương trình đường thẳng ()cắt (d1),(d2) và trục Ox lần
lượt tại các điểm A, B, C sao cho B là trung điểm AC
Câu 9.b (1,0 điểm ).Giải phương trình: 1loglog3log1 399 xxx
Đáp án
Câu Nội dung Điểm
Câu 1a Tập xác định: D = R \ –1
2
/
1
4
x
y, Dxy ,0
/
0,25
Vì:

1
3
lim
1
x
x
x
và

1
3
lim
1
x
x
x
nên: x = –1 là tiệm cận đứng
Vì: 1
1
3
lim

x
x
x và 1
1
3
lim

x
x
x
nên: y = 1 là tiệm cận ngang
0,25
Bảng biến thiên và kết luận 0,25
Đồ thị 0,25
Câu 1b Gọi
1
3
;m
m
mM thuộc đồ thị, có I(–1 ; 1)
2
2
1
16
1
m
mIM
0,25
162
1
16
12
2
m
mIM 22
( Tương ứng xét
0,
16 t
t
ttg và t = (m + 1)2 và lập được
bảng biến thiên
0,25
IM nhỏ nhất khi 22IM
Khi đó (m + 1)2 = 4
0,25
Tìm được hai điểm
1;1
1M và
3;3
2M 0,25
Câu 2 Giải phương trình: 3
1
2
sin
2
cos
2
4sin2cos
2
x
x
xx
Điều kiện:
2
1
2sin
12sin
012sin2sin2 2
x
x
xx
0,25
3
1
2
sin
2
sin
2
4sin2cos
2
x
x
xx
xxxx 4cos2sin34sin2cos
xxxx 4sin4cos32sin32cos
0,25
6
4cos
3
2cos
xx
2
6
4
3
2
2
6
4
3
2
kxx
kxx
kx
4
3
2
6
kx 0,25
So lại điều kiện được nghiệm phương trình đã cho
3
2
6
kx 0,25
Câu 3 Giải hệ phương trình:
021
01
2
2
yyxx
yxyx
021
01
2
2
yyxx
yxyx
02
1
2
yyxyxy
yxyx
012
1
2
yxyx
yxyx
( Vì: y = 0 không là nghiệm của hệ)
012
1
2
2
yxyx
yxyx
01
1
2
2
yx
yxyx
1
1
2
yx
yxyx
1
1
2
yx
yx
xy
xx
1
11
2
xy
xx
1
0
2
xy
xx
1
10
Nghiệm của hệ: (0 ; 1) , ( –1 ; 2)
Câu 4
dxxxxA 2sin1lncossin
4
0
dxxxxxA 2
4
0
cossinlncossin
dxxxxxA cossinlncossin2
4
0
(Vì:
4
;0,0cossin
xxx )
0,25
Đặt
dxxxdv
xxu
cossin
cossinln suy ra:
xxv
dx
xx
xx
du
sincos
cossin
sincos
0,25
4
0
4
0sincoscossinlncossin2
dxxxxxxxA
0,25
4
0
cossin2ln22
xxA
A =
122ln22
2222ln2 A
0,25
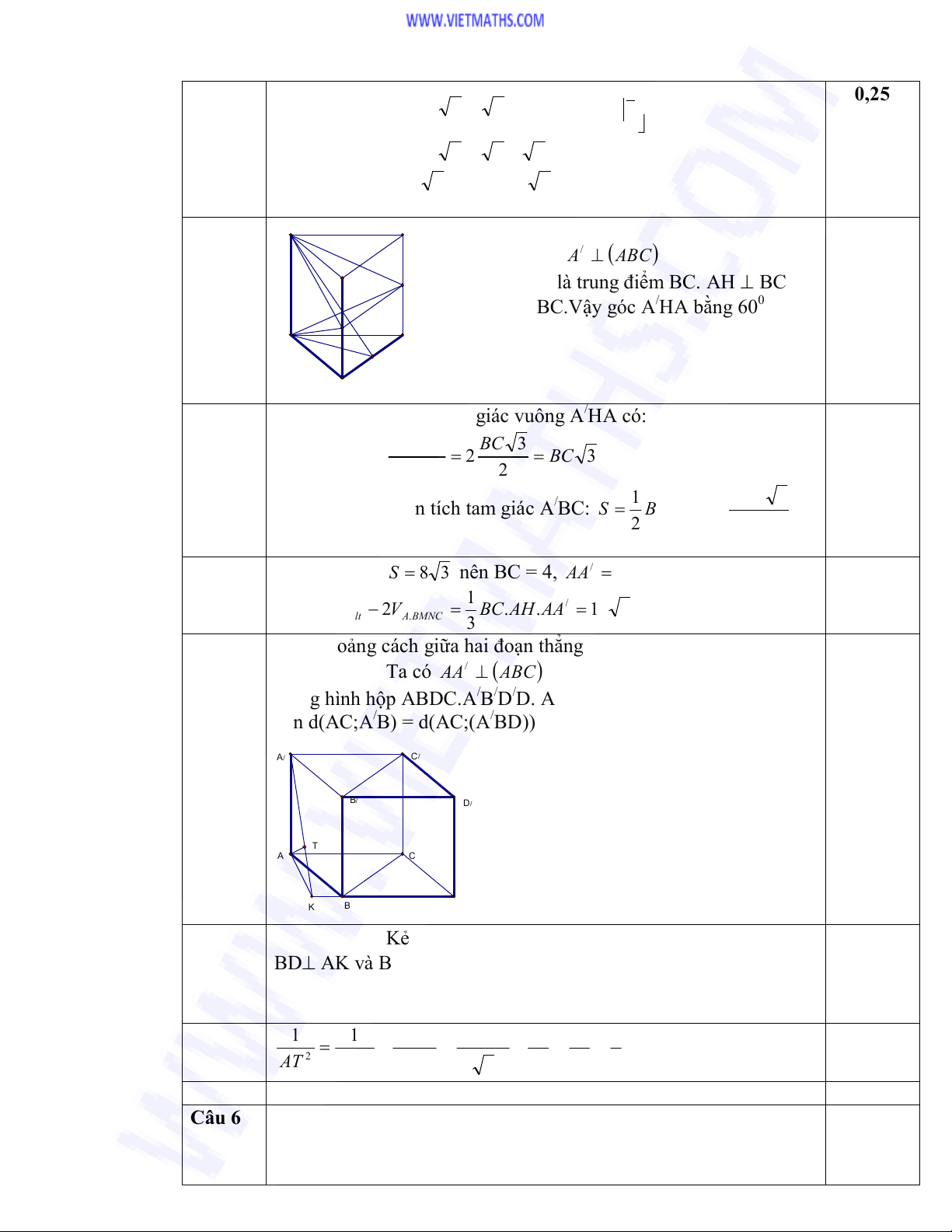
Câu 5a
Ta có
ABCAA
/
Gọi H là trung điểm BC. AH BC
nên A/H BC.Vậy góc A/HA bằng 600
Trong tam giác vuông A/HA có:
3
2
3
2
60
cos
0
/BC
BCAH
HA
Diện tích tam giác A/BC:
2
3
.
2
12
/BC
HABCS
38S nên BC = 4, 660tan 0/ AHAA
316..
3
1
2/
.
/ AAAHBCVVV BMNCAlt
AMNA
Câu 5b Tính khoảng cách giữa hai đoạn thẳng A/B và AC
Ta có
ABCAA
/
Dựng hình hộp ABDC.A/B/D/D. AC//BD nên AC//(A/BD) A/B
nên d(AC;A/B) = d(AC;(A/BD)) = d(A;(A/BD))
0,25
Kẻ AK BD (K BD)
BD AK và BD AA/ nên BD (A/AK) (A/BD) (A/AK)
Kẻ AT A/K (TA/K) AT(A/BD)
AT=d(A;(A/BD)) = d(AC;A/B)
0,25
9
1
36
4
6
1
32
1111
222/22 AAAKAT hay AT = 3 0,5
Câu 6 Gọi 1
x , 2
x , 3
x là nghiệm phương trình
07329232 2223 mmxmmxmx
Tìm giá trị nhỏ nhất và giá trị lớn nhất của
M
N
H
C
/
B
/
A
/
C
B
A
T
K
D
/
D
C
/
B
/
A
/
C
B
A
Hay A =
2112 2 mmmf m
3;2
114
/ mmf ,
0
/mf
3;2
4
11 m
0,25
282 f và
493 f
Vậy 49max
A khi m = 3 và 28min
A khi m = 2
0,25
PHẦN TỰ CHỌN
A. Theo chương trình chuẩn
Câu 7a Cho tam giác ABC với B(1;–2),phương trình đường cao vẽ từ
A là d: x –y + 3 = 0.Tìm tọa độ A ,C của tam giác.Biết C thuộc
đường thẳng :2x + y –1 = 0 và diện tích tam giác ABC bằng 1
BC qua B và vuông góc d nên BC có phương trình: x + y + 1 = 0
Tọa độ C là nghiệm của hệ
3
2
01
012
y
x
yx
yx Vậy: C(2 ; –3)
0,25
daaA 3; .
2
42
;
a
BCAd ,2BC .Theo giả thiết ta
có:
1;.
2
1BCAdBC hay 1
2
42
.2.
2
1
a
0,25
Hay
3
1
2421
2
42
.2.
2
1
a
a
a
a
Với a = –1 thì A(–1 ; 2), với a = –3 thì A(–3 ; 0)
0,5
Câu 8a Gọi C(a ; b; 0), tam giác ABC cân tại C nên trung điểm
H(3 ; 3 ; 0) của AB cũng là chân đường cao vẽ từ C.
0,25
Theo giả thiết ta có:
58.
2
1CHAB
BCAC
5833.64016
2
1
16311635
22
2222
ba
baba
0,5
321
2
3
2
2
2
1xxxxxxA
Phương trình:
07329232 2223 mmxmmxmx (*)
Có nghiệm 1
3x
Nên (*)
0732121 22 mmmxx
10073212
1
22 mmxmx
x
0,25
(1) có hai nghiệm 21;xx khi:
07321 2
2 mmm
065
2 mm 32
m
321
2
3
2
2
2
1xxxxxxA = 21
2
2
2
11xxxx
=
1
21
2
21 xxxx =
63222 2
2 mmm
0,25