TRƯỜNG ĐẠI HỌC SƯ PHẠM HUẾ
KHOA TOÁN
--------
TỪ CÂU HỎI TRUYỀN THỐNG ĐẾN CÂU HỎI TRẮC
NGHIỆM KHÁCH QUAN
CHỦ ĐỀ: SỐ PHỨC
SINH VIÊN: LÊ QUANG NHẬT
MSV: 13S1011108
LỚP TOÁN 4T
GIÁO VIÊN: NGUYỄN ĐĂNG MINH PHÚC
Huế, tháng 04 năm 2017
Sinh viên: Lê Quang Nhật
GVHD: Nguyễn Đăng Minh Phúc
Môn: LLDH Toán NC và ĐG trong DH Toán
Chủ đề: Số phức
Bài toán 1: Trong mặt phẳng phức, cho và lần lượt là hai điểm biểu diễn hai số phức
và . Tìm số phức có phần thực dương được biểu diễn bởi điểm
biết rằng tam giác vuông cân tại .
Bài giải:
và lần lượt biểu diễn cho hai số phức và nên
. Gọi thỏa mãn yêu cầu bài toán, lúc đó biểu diễn cho số phức
.
Ta có
Tam giác vuông cân tại nên
⇔
⇔
⇔
⇔
⇔
⇔
⇔
loại ần t ực dương
Vậy số phức được biểu diễn bởi điểm thỏa mãn yêu cầu bài toán là
Đây là dạng toán t ường hay gặp ở lớp 12, ở đây điều chúng ta muốn biết là học sinh
có thể nhớ và hiểu cách biểu diễn hình học của một số phức ay k ông. Trước hết học sinh
sử dụng các t ông tin được viết để thành lập một mô hình toán, bước này phụ thuộc vào kiến
thức về biểu diễn hình học của số phức. Giả sử các học sinh có những kiến thức này thì sẽ vẽ
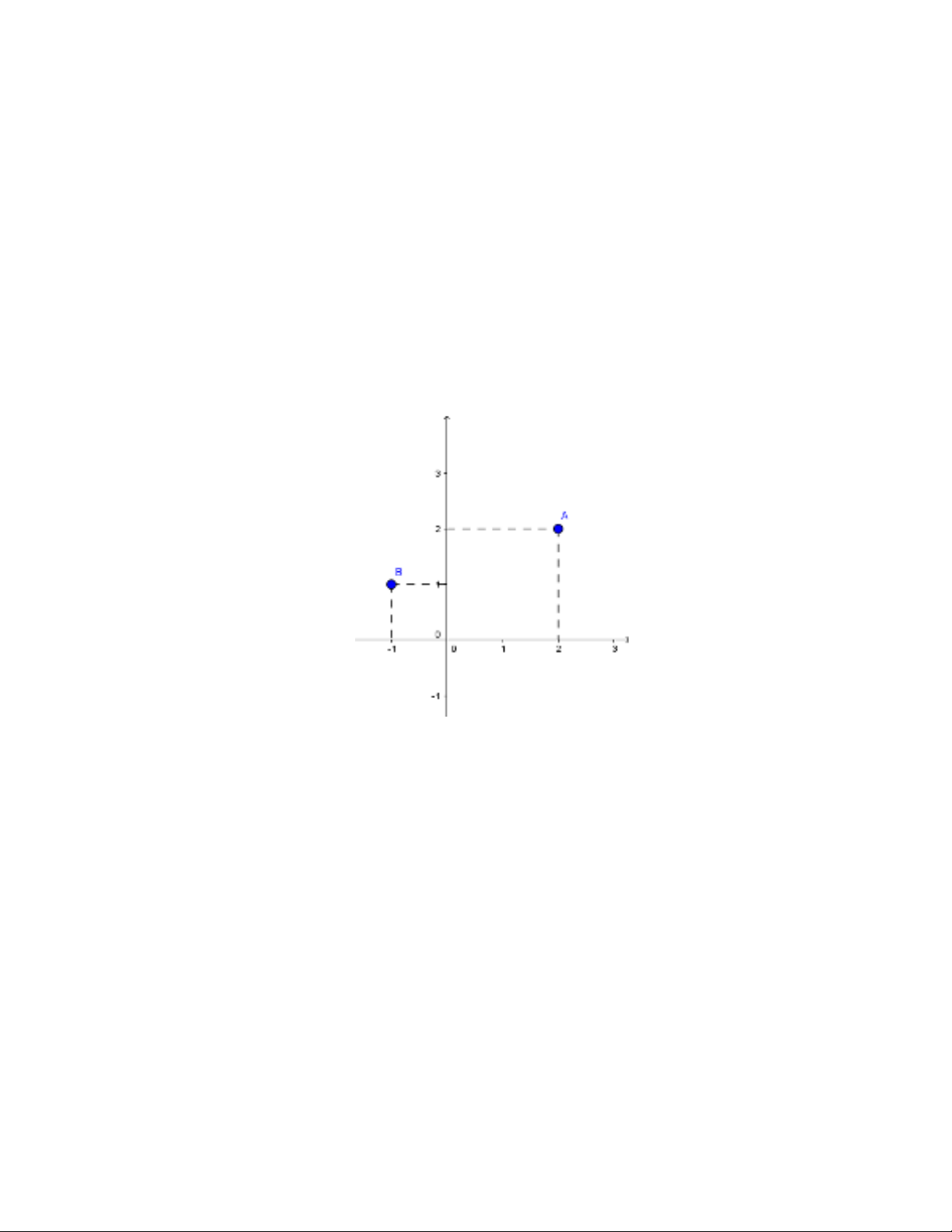
một n n ư sau:
Sau đó ọc sinh sẽ gọi tọa độ của điểm biểu diễn cho số phức cần tìm rồi từ
giả thiết bài toán tam giác vuông cân tại học sinh có được hệ ương tr n sau:
Giải hệ ương tr n trên ta sẽ t m được tọa độ điểm , từ đó suy ra số phức cần tìm
sau k i đối chiếu điều kiện bài toán.
Rõ ràng nếu các em thất bại ngay ở bước đầu tiên là không biết cách biểu diễn hình
học của số phức thì không thể giải quyết được bài toán trên. Đặc trưng của bài toán này là
học sinh không thể giải đơn t uần bằng các biểu thức đại số mà phải thông qua hình học, từ
đó ta t ấy được tầm quan trọng của biễu diễn hình học của số phức. Nếu chỉ là câu hỏi tự
luận chúng ta sẽ không phản án được khả năng của học sinh về các khía cạnh trong bài toán
gốc, do đó c úng ta sẽ sử dụng các câu hỏi trắc nghiệm có liên quan n ư sau:
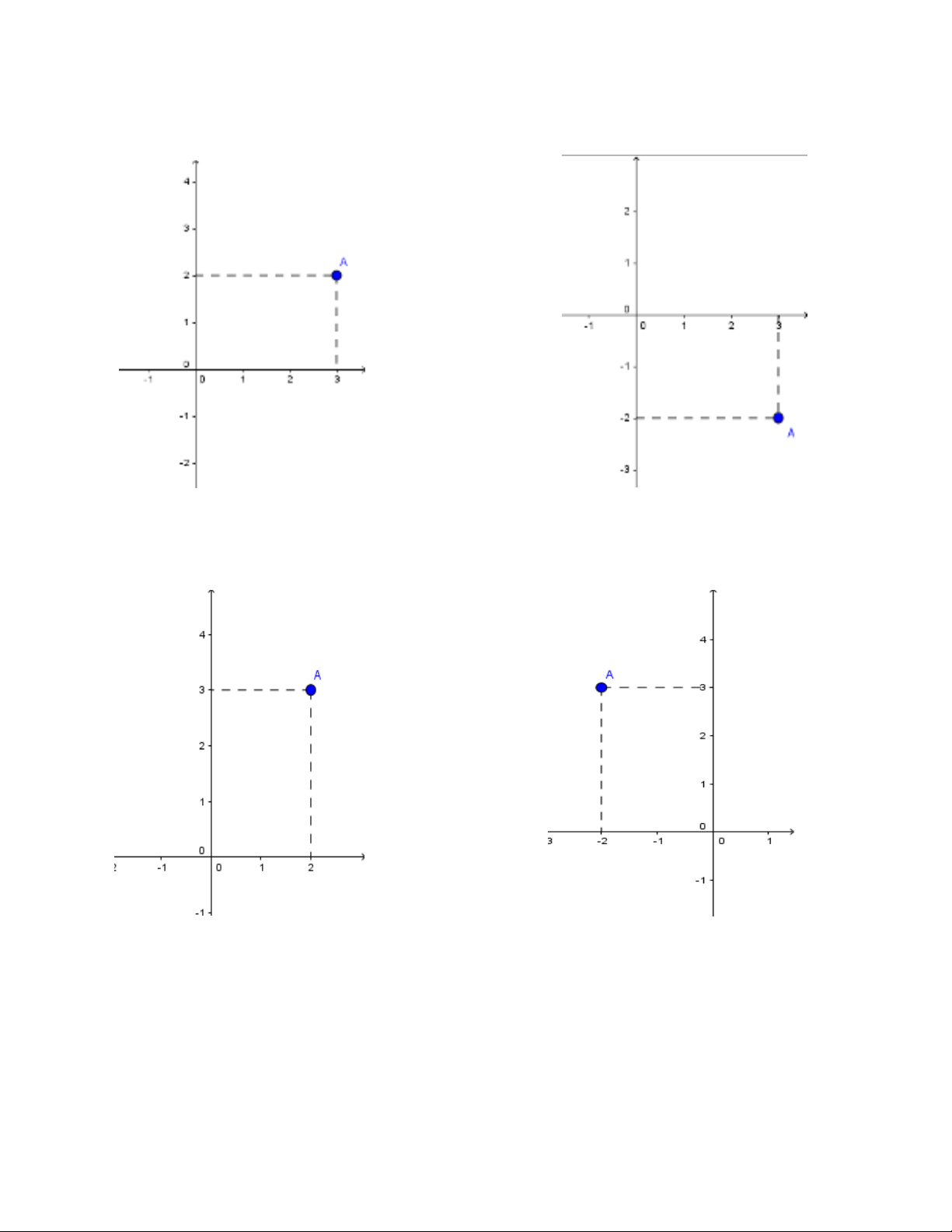
Câu 1: Trong các n dưới đây, n nào có điểm A biểu diễn cho số phức ?
A B
C D
Đáp án B
( Ở đây ọc sinh cần nhớ kiến thức: "Số phức t có điểm biểu diễn là " là
có thể trả lời được câu hỏi này)
Câu 2: Cho là điểm biểu diễn số phức và là điểm biểu diễn số phức
. Mện đề nào sau đây đúng?
A. Hai điểm và đối xứng với nhau qua trục hoành.
B. Hai điểm và đối xứng với nhau qua trục tung.
C. Hai điểm và đối xứng với nhau qua gốc tọa độ .
D. Hai điểm và đối xứng với n au qua đường thẳng .
Đáp án A
( Trong câu này ta thấy 2 số phức và có phần ảo đối n au nên ai điểm biểu diễn tương
ứng của chúng sẽ đối xứng với nhau qua trục thực ( hay còn gọi là trục hoành ), học sinh
t ường hay nhầm lẫn điều này nên một số sẽ chọn đá án B
Bước thứ 2 là từ giả thiết bài toán ta đưa ề biểu thức toán học, ta có thể xây dựng một
câu hỏi để kiểm tra khả năng đó.
Câu 3: Cho tam giác vuông cân tại hệ thức nào sau đây đúng ?
A.
B.
C.
D.
Đáp án B
( Do tam giác vuông cân tại nên và , trong các ương án được
đưa ra trước hết học sinh có thể loại bỏ đá án D
tức là tam giác vuông
tại . Tiếp theo học sinh sẽ phát hiện đá án A à C gần giống nhau nên sẽ phân vân một
trong hai đá án, ở đá án C ai ectơ
và
bằng nhau ( vô lý ). Vì vậy đá án c ín
xác là đá án B .
Bước cuối cùng là kiểm tra lại giả thiết của bài toán, ở phần này học sinh phải có kiến
thức về số phức có phần thực, phần ảo dương ay âm , cụ thể ta có thể đưa câu ỏi trắc
nghiệm sau: