 !""#
Trang
PHN I. TÓM TT GIÁO KHOA
A. ðI S
I. PHƯƠNG TRÌNH VÀ BT PHƯƠNG TRÌNH
1. Phương trình bc hai
Cho phương trình bc hai
   
+ + = ≠
(3) có

= −
.
1)
<
: (3) vô nghim. 2)
=
: (3) có nghim kép

= −
.
3)
>
: (3) có hai nghim phân bit


 
− ± − ± −
= =
.
ðnh lý Vi–et (thun và ño)
1) Cho phương trình
 
+ + =
có hai nghim

thì
= + = −
= =
.
2) Nu bit

= +
=
thì

là nghim ca phương trình

− + =
.
2. Bng xét du ca tam thc bc hai f(x) = ax
2
+ bx + c

> >

< >
x
−∞
x
1
x
2
+∞
x
−∞
x
1
x
2
+∞
f(x) + 0 – 0 + f(x) – 0 + 0 –

> =

< =
x
−∞
x
kép
+∞
x
−∞
x
kép
+∞
f(x) + 0 + f(x) – 0 –

> <

< <
x
−∞
+∞
x
−∞
+∞
f(x) + f(x) –
3. Bng bin thiên ca hàm s bc hai f(x) = ax
2
+ bx + c
1) a > 0: 2) a < 0:
x
−∞

−
+∞
x
−∞

−
+∞

+∞
+∞

Cð
CT
−∞
−∞
4. So sánh nghim ca tam thc bc hai f(x) = ax
2
+ bx + c vi mt s
1)

α < ⇔ < α <
3)

>
α > ⇔ α < <
> α
2)
 
< α < < β
α β < ⇔ α < < β <
4)

>
α > ⇔ < < α
< α
7. Phương trình ñi s bc cao
Phương trình bc n tng quát có dng
  
−
−
+ + + + = ≠
.
Thông thưng ta ch gii ñưc phương trình bc 3 tr lên bng cách nhm nghim.
7.1. Phương trình bc ba: ax
3
+ bx
2
+ cx + d = 0 (
≠
) (4)
1) Phương pháp gii
Bưc 1. Nhm 1 nghim
= α
ca (4) (bm máy tính).
Bưc 2. Chia
  
+ + +
cho (
− α
) (dùng sơ ñ Horner), ñưa (4) v phương trình tích:
   
− α + + =
.
2) Sơ ñ Horner
a b c d
α
a
α
a + b = B
α
B + c = C
α
C + d = 0
 !""#
Trang
7.2. Phương trình bc bn ñc bit
a) Phương trình trùng phương ax
4
+ bx
2
+ c = 0 (
≠
) (5)
Phương pháp gii: ðt t = x
2
,
≥
. (5)
⇔
at
2
+ bt + c = 0.
b) Phương trình có dng (x + a)(x + b)(x + c)(x + d) = e vi a + c = b + d (6)
Phương pháp gii: ðt t = (x + a)(x + c), ñưa (6) v phương trình bc 2 theo t.
c) Phương trình có dng (x + a)
4
+ (x + b)
4
= c (7)
Phương pháp gii: ðt
+
= +
, ñưa (7) v phương trình trùng phương theo t.
d) Phương trình trùng phương ax
4
+ bx
3
+ cx
2
±
bx + a = 0 (
≠
) (8)
Phương pháp gii
Bưc 1. Chia 2 v cho x
2
,

⇔ + + ± + =
.
Bưc 2. ðt
= ±
, ñưa (8) v phương trình bc hai theo t.
8. Bt phương trình hu t


>
Bưc 1. Lp trc xét du chung cho P(x) và Q(x).
Bưc 2. Da vào trc xét du ñ kt lun nghim.
9. ðiu kin ñ phương trình có nghim trong khong (a; b)
a) ðnh lý 1
Hàm s f(x) liên tc trên [a; b] tha

<
thì phương trình f(x) = 0 có nghim trong (a; b) (ngưc li không ñúng).
b) ðnh lý 2
Hàm s

liên tc trên [a; b] và có

>
(hoc

<
) trong khong
 
thì phương trình

=
có không
quá 1 nghim trong
 
.
II. PHƯƠNG TRÌNH VÀ BT PHƯƠNG TRÌNH VÔ T.
1. Các hng ñ ng thc c!n nh
1)


≥
= =
− <
; 2)


± + = ± +
;
3)
(
)
 
± = ± ± ±
; 4)
 
 
+ + = + −
.
2. Phương trình và bt phương trình cha giá tr tuyt ñi
1)
= ⇔ = ⇔ = ±
; 2)
≥
= ⇔
= ±
; 3)
< ⇔ − < <
;
4)
>
< ⇔
− < <
; 5)
>
⇔ <
≥
∨
< − ∨ >
.
3. Phương trình và bt phương trình vô t
1)
≥ ∨ ≥
= ⇔
=
; 2)
= ⇔ ≥ ∧ =
; 3)
+ = ⇔ = =
;
4)
(
)
≥ ∧ ≥ ∧ ≥
+ = ⇔
+ =
ñưa v dng
=
; 5)
≥
> ⇔
>
;
6)
≥ ∧ >
< ⇔
<
; 7)
≥
<
> ⇔ ∨
≥>
; 8)
< ⇔ <
;
9)


+
+
= ⇔ =
; 10)

≥ ∨ ≥
= ⇔
=
; 11)


≥
= ⇔
=
.
III. PHƯƠNG TRÌNH – BT PHƯƠNG TRÌNH MŨ VÀ LOGARIT
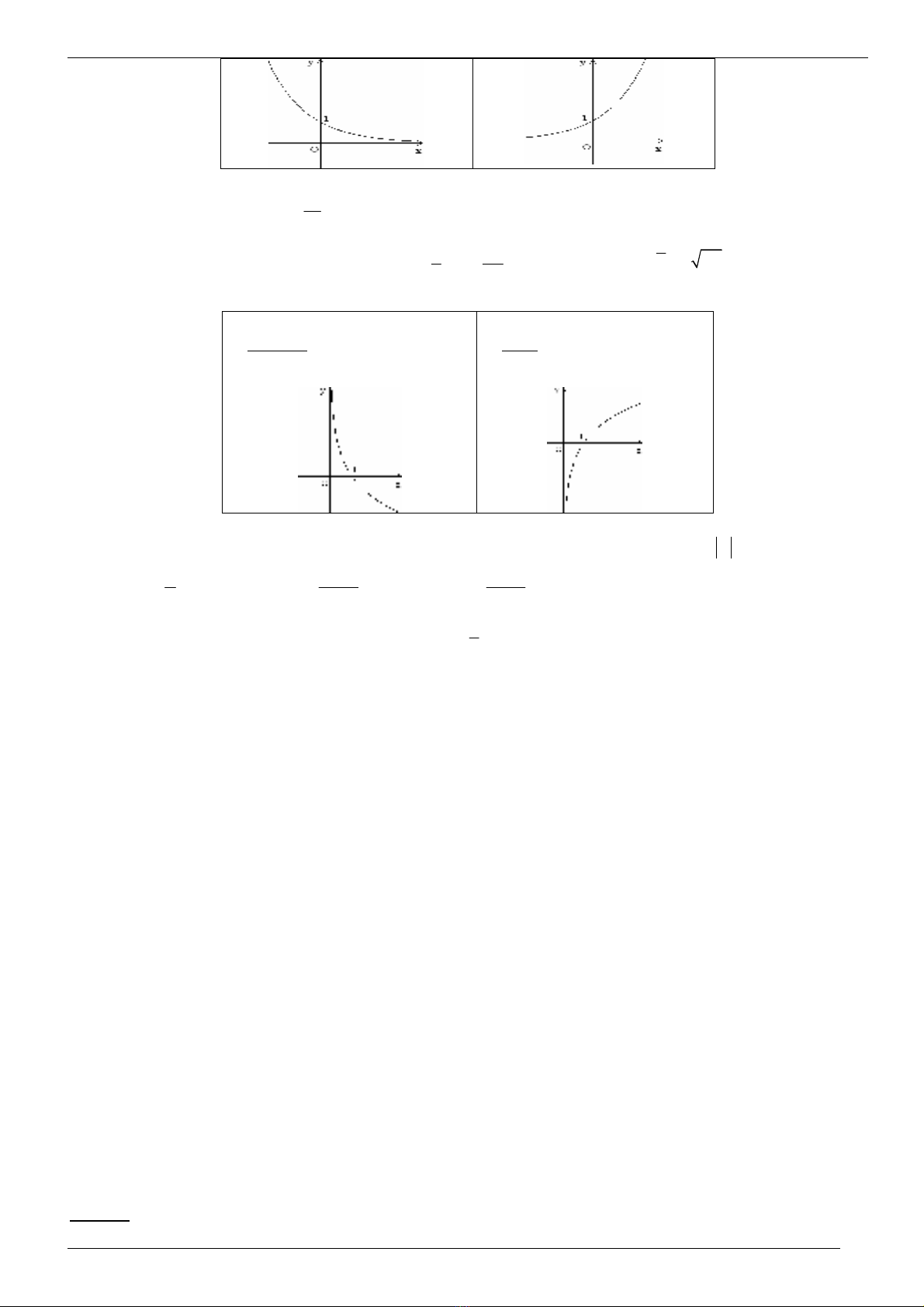
1. Hàm s mũ y = a
x
(a > 0)
1) Min xác ñnh
=
ℝ
2) Min giá tr
! "
= +∞
3) 0< a< 1: Hàm nghch bin trên
ℝ
#$% #$%
→−∞ →+∞
= +∞ =
4) a > 1: Hàm s ñng bin trên
ℝ
#$% #$%
→−∞ →+∞
= = +∞
 !""#
Trang
Mt s công thc c!n nh (gi s$ các ñiu kin ñư%c th&a)
1)

= ≠
; 2)
−
=
; 3)
% %
+
=
; 4)
% %
−
=
;
5)
(
)
% %
=
; 6)
% % %

=
; 7)
%
%
%
=
; 8)
%
%
=
.
2. Hàm s logarit y = log
a
x

< ≠
: y = log
a
x
⇔
x = a
y
1) Min xác ñnh
"
= +∞
2) Min giá tr
!
=
ℝ
3) 0 < a < 1: Hàm nghch bin trên D
#$% #$%
+
→+∞
→
= +∞ = −∞
4) a > 1: Hàm s ñng bin trên D
#$% #$%
+
→+∞
→
= −∞ = +∞
Mt s công thc c!n nh (gi s$ các ñiu kin ñư%c th&a)
1)
#&'
=
; 2)
#
(
=
; 3)
#&' #&'
=
; 4)

#&'  #&'
=
;
5)
#&' #&'
α
β
β
=
α
; 6)
#&'
#&'
=; 7)
#&'
#&'
#&'
=; 8)
#&' #&' #&'
=;
9)
#&'  #&' #&'
= + ; 10)
#&' #&' #&'
= −
.
3. Phương trình và bt phương trình mũ cơ bn
1)
 #&'
>
=
⇔
=
< ≠
; 2)
'
=
⇔
 '
 '
=
∀ ∈ ∈
< ≠
=
ℝ ℝ
;
3)
 #&'

>
<
>
⇔
≤
< <
∀ ∈ ∈
ℝ ℝ
; 4)

 #&'

>
>
>
⇔
≤
>
∀ ∈ ∈
ℝ ℝ
;
5)
'
 '
>
⇔ <
< <
; 6)
 '
 '
>
⇔ >
>
.
4. Phương trình và bt phương trình logarit cơ bn
1)
#&' 

=
⇔ =
< ≠
; 2)
#&'  #&' ' 
 '
= >
⇔
< ≠ =
;
3)
#&' 

>
⇔ < <
< <
; 4)
#&' 

>
⇔ >
>
;
5)
#&'  #&' '
>
< <
⇔
0 < f(x) < g(x); 6)
#&'  #&' '
>
>
⇔
f(x) > g(x) > 0.
IV. H' PHƯƠNG TRÌNH
Nh(c li: H phương trình bc nht hai )n
+ =
+ =
.
 !""#
Trang
ðt
=
,
=
,
=
.
1)
≠
: H phương trình có nghim duy nht
=
=
.
2)
= ≠
hoc
≠
: H phương trình vô nghim.
3) D = D
x
= D
y
= 0: H có vô s nghim tha a
1
x + b
1
y = c
1
hoc a
2
x + b
2
y = c
2
.
1. H phương trình ñ ng cp
Phương pháp chung
1) Nhn xét y = 0 có tha h phương trình không, nu có tìm x và thu ñưc nghim.
2) Vi
≠
, ñt

=
thay vào h phương trình gii tìm t, y và x.
3) Th li nghim.
Ví d*:

 
+ + =
− + =
,
)
  
− =
+ =
.
2. H phương trình ñi xng loi I (c 2 phương trình ñu ñi xng)
Phương pháp chung
1) Xét ñiu kin, ñt S = x + y, P = xy
 
≥
.
2) Gii h tìm S, P ri dùng Vi–et ño tìm x, y.
Ví d*:
 

+ =
+ =
.
3. H phương trình ñi xng loi II
a. Dng 1 (ñ+i v trí x và y thì phương trình này tr, thành phương trình kia)
Phương pháp chung
Cách 1. Tr hai phương trình cho nhau, ñưa v phương trình tích, gii x theo y (hay ngưc li) ri th vào mt trong hai
phương trình ca h.
Ví d*:


+ =
+ =
,


+ + − =
+ + − =
.
Cách 2 (nu cách 1 không th-c hin ñư%c)
Cng và tr l n lưt hai phương trình ñưa v h mi tương ñương gm hai phương trình tích (thông thưng tương ñương vi 4
h mi).
Ví d*:

− =
− =
.
Cách 3. S dng hàm s ñơn ñiu ñ suy ra x = y.
Ví d*:


+ + − =
+ + − =
,
*$
*$
=
=
.
b. Dng 2 (ch có 1 phương trình ñi xng)
Cách 1
ðưa phương trình ñi x!ng v dng tích, gii y theo x th vào phương trình còn li.
Ví d*:
 
− = −
− − =
.
Cách 2
Thưng ñưa v dng
 
= ⇔ =
vi hàm f(x) ñơn ñiu.
Ví d*:
( (

− = −
− − =
.
4. H phương trình cha mũ – logarit và dng khác
Tùy tng trưng hp c th ch"n phương pháp thích hp (thưng dùng phương pháp th).
V. BT ð.NG TH/C CAUCHY
1. Bt ñ ng thc Cauchy hai s
Cho hai s không âm a và b, ta có:

+
≥
ð#ng th!c xy ra khi a = b.
 !""#
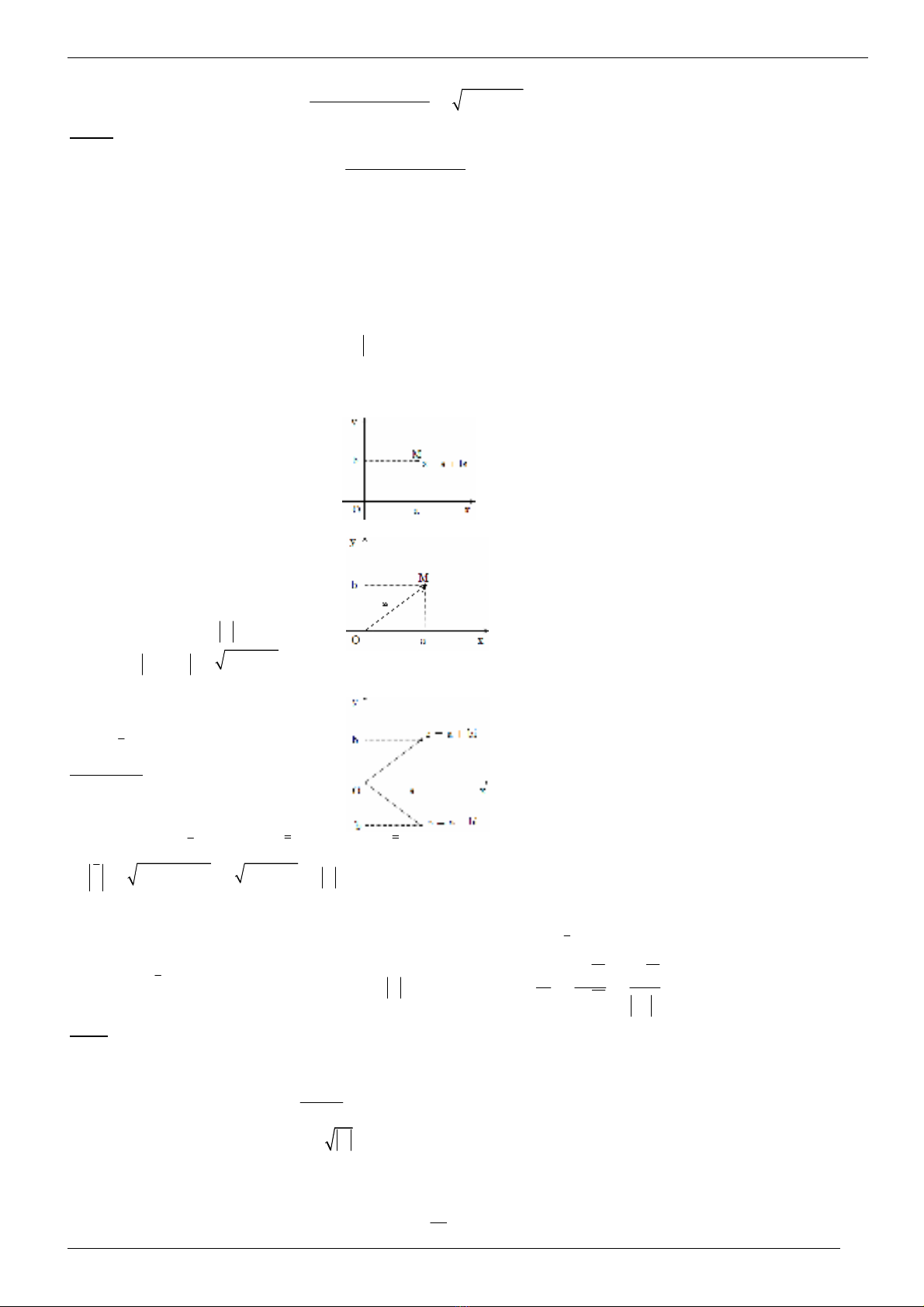
Trang
2. Bt ñ ng thc Cauchy n s
Cho n s không âm a
1
, a
2
,…, a
n
ta có:


+ + + ≥
. ð#ng th!c khi a
1
= a
2
= … = a
n
.
Chú ý:
Bt ñ#ng th!c Cauchy ngưc


+ + +
≤
.
VI. S PH/C
1. S phc và các phép tính cơ bn
a) ðnh nghĩa s phc
M$i biu th!c dng
$
+
, trong ñó
∈
ℝ
,
$
= −
ñưc g"i là mt s ph!c.
ði vi s ph!c
+ $
= +
, ta nói a là ph n thc, b là ph n o ca z.
Tp hp các s ph!c ký hiu là
{
}
$   $
= + ∈ = −ℂ ℝ
.
b) S phc bng nhau
$ $
+ = + ⇔ =
và
=
.
c) Biu di1n hình h2c s phc
M$i s ph!c
+ $
= +
hoàn toàn
ñưc xác bi mt cp s thc
"
.
ðim M(a; b) trong h t"a ñ vuông góc
Oxy ñưc g"i là ñim biu di%n s ph!c
+ $
= +
.
d) Môñun ca s phc
Gi s s ph!c
+ $
= +
ñưc bi%u
di%n bi ñim M(a; b) trên mt ph#ng
t"a ñ Oxy.
ð dài ca
,-

ñưc g"i là môñun ca
s ph!c z và ký hiu là
+
.
Vy
$
+ = +
.
e) S phc liên h%p
Cho s ph!c
+ $
= +
. Ta g"i
$
−
là s phc liên h%p ca z và ký
hiu là
+ $
= −
.
NHN XÉT
1) Trên mt ph#ng t"a ñ ñim biu di%n
hai s ph!c liên hp ñi x!ng vi nhau
qua trc Ox.
2)
+ $ + $ + $
= + ⇒ = − ⇒ = +
hay
+ +
=
.
3)
+  +
= + − = + =
.
f) Các phép tính cơ bn
1) (a + bi) + (c + di) = (a + c) + (b + d)i; 2) (a + bi) – (c + di) = (a – c) + (b – d)i.
3) (a + bi)(c + di) = (ac – bd) + (ad + bc)i; 4)
+ +  $  $ 
+ = + + − =
;
5)
++  $ $ +
= + − = + =
; 6)
+ + + + +
++ +
+
= =
,
+
≠
.
Chú ý
i) Phép nhân hai s ph!c ñưc thc hin theo quy t&c nhân ña th!c ri thay
$
= −
trong kt qu nhn ñưc.
ii) Phép cng và phép nhân các s ph!c có tt c các tính cht ca phép cng và phép nhân các s thc.
iii) Trong thc hành, ñ tính thương
$
$
+
+
, ta nhân c t và m'u vi s ph!c liên hp ca
$
+
.
4i) S thc a âm có hai căn bc hai là
$
±
.
g) Phương trình bc hai vi h s th-c
Cho phương trình bc hai ax
2
+ bx + c = 0 vi
 
∈
ℝ
,
≠
. Bit s ca phương trình là

= −
.
a) Khi
=
, phương trình có mt nghim thc

= −
.