Đ H A 2DỒ Ọ
Đ H A 2DỒ Ọ
Đ
ĐƯ
ƯNG CONGỜNG CONGỜ
Gi ng viên : Bùi Ti n Lênả ế
Trang
Trang 2
2
Phân lo iạ
Phân lo iạ
Quan đi m toán h cể ọ
- Đưng cong ờđưc bi u di n b ng hàm sợ ể ễ ằ ố
- Đưng cong ờđưc bi u di n b ng phợ ể ễ ằ ương trình tham số
Quan đi m thi t kể ế ế
- Đưng cong CAD (Computer Aided Design)ờ
Đ
Đư
ưng cong ờng cong ờđư
đưc bi u di n ợ ể ễ
c bi u di n ợ ể ễ
b ng hàm sằ ố
b ng hàm sằ ố
Trang
Trang 4
4
Bài toán
Bài toán
Input
Hàm s y = f(x)ố
Mi n ềđ i s [xố ố min, xmax]
Output
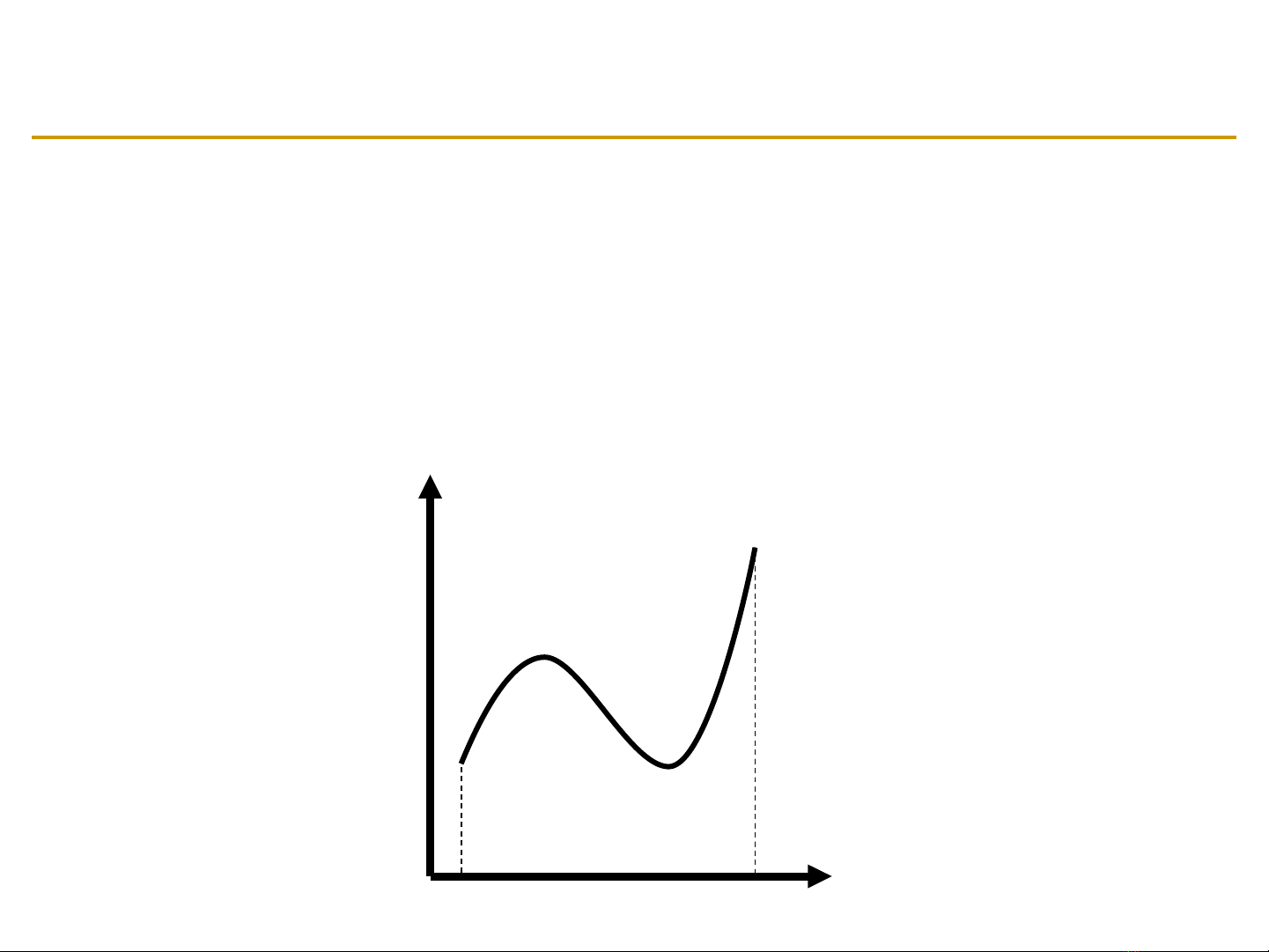
Đ th hàm sồ ị ố
xmax
xmin
y=f(x)
Trang
Trang 5
5
Thu t toánậ
Thu t toánậ
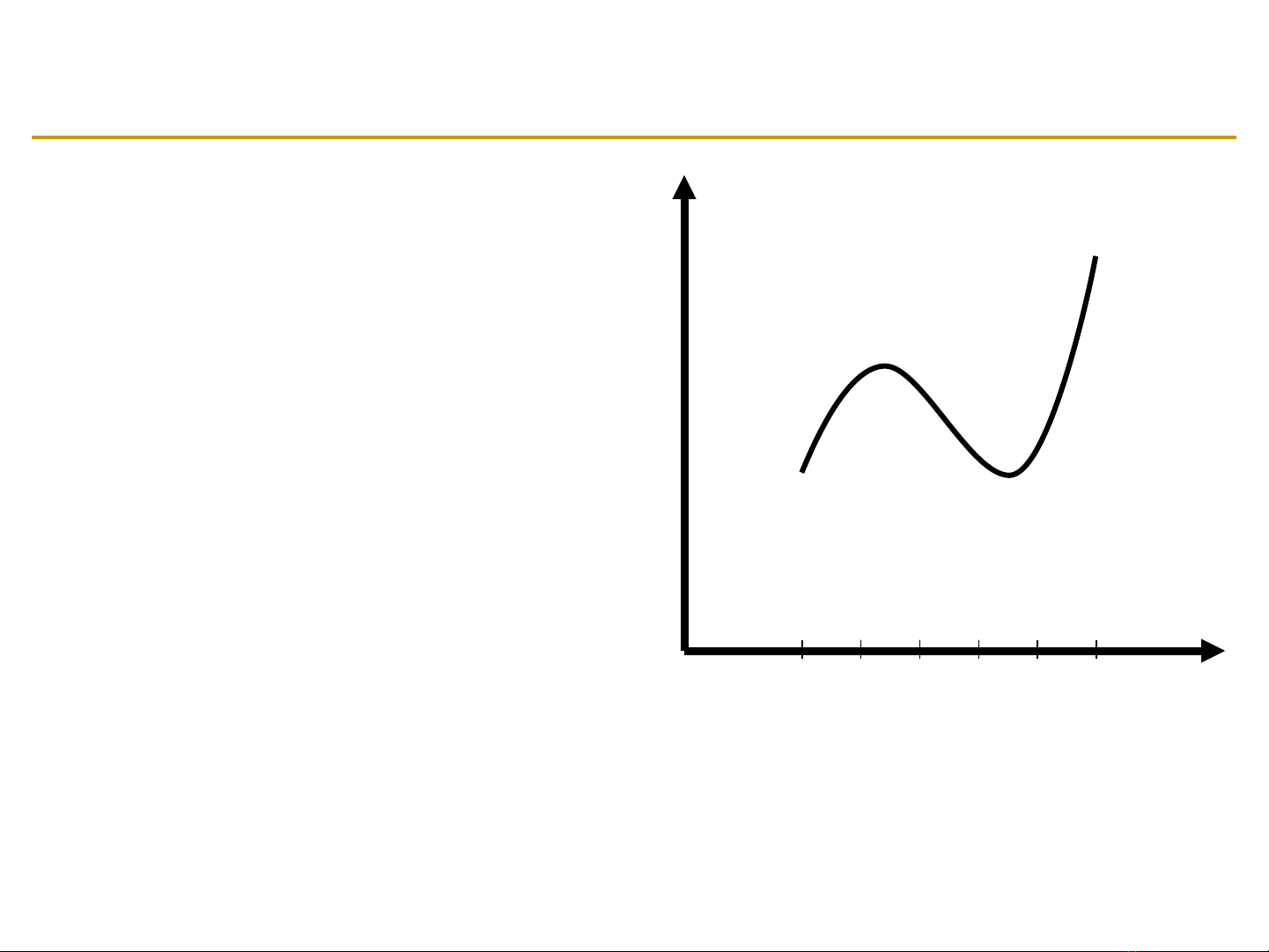
Bưc 1ớ : Chia mi n ềđ i s ra N ố ố
đo n b ng nhauạ ằ
x0x1x2xN-1 xN
xmin xmax