Giới thiệu tài liệu
Tích phân mặt loại II là một công cụ toán học thiết yếu trong giải tích vector, đóng vai trò quan trọng trong việc định lượng sự truyền tải của một trường vector qua một bề mặt định hướng. Khái niệm này có ý nghĩa sâu sắc trong nhiều lĩnh vực khoa học và kỹ thuật, từ việc mô tả dòng chảy chất lỏng (thông lượng) qua một mặt cắt, thông lượng nhiệt qua một vật thể, đến các ứng dụng trong điện từ học. Hiểu rõ về tích phân mặt loại II không chỉ củng cố nền tảng toán học mà còn mở ra khả năng phân tích và giải quyết các bài toán vật lý phức tạp, nơi các đại lượng như thông lượng cần được tính toán chính xác. Tài liệu này cung cấp một cái nhìn tổng quan về định nghĩa, phương pháp tính toán và các định lý liên quan, đặc biệt là Định lý Gauss, nhằm trang bị kiến thức nền tảng vững chắc cho người học.
Đối tượng sử dụng
Sinh viên ngành toán, vật lý, kỹ thuật đang theo học các môn giải tích cao cấp, đặc biệt là giải tích vector, và những ai cần ứng dụng tích phân mặt trong các bài toán thực tế.
Nội dung tóm tắt
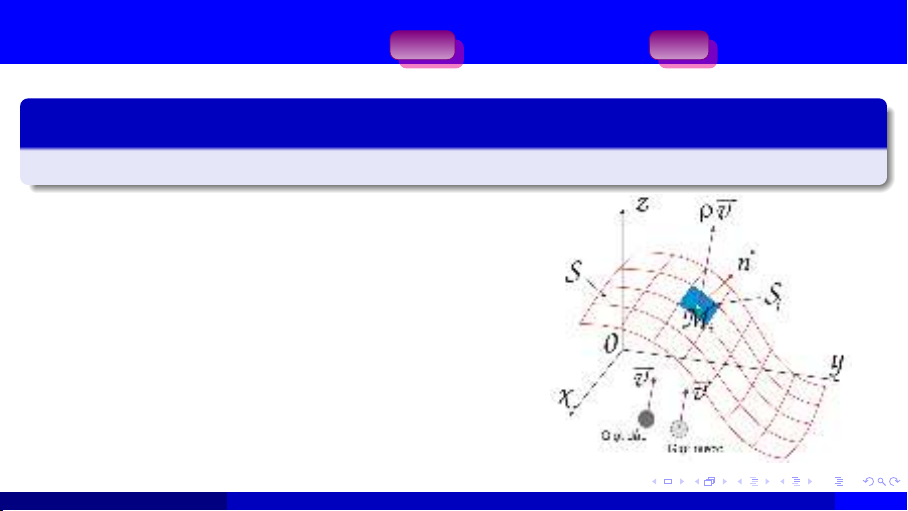
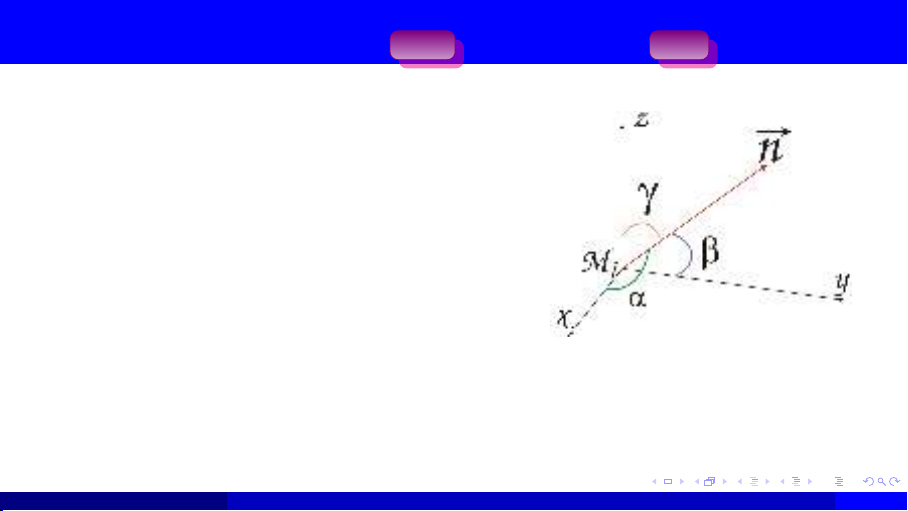
Tài liệu này giới thiệu chi tiết về tích phân mặt loại II, bắt đầu bằng việc đặt vấn đề từ một bài toán vật lý cụ thể: tính toán thông lượng chất lỏng chảy qua một bề mặt cho trước. Từ đó, định nghĩa toán học của tích phân mặt loại II được xây dựng dựa trên tổng Riemann, làm rõ vai trò của các hàm thành phần của trường vector và véc-tơ pháp tuyến đơn vị của bề mặt định hướng. Các phương pháp tính toán được trình bày một cách rõ ràng, bao gồm việc xác định các thành phần của trường vector (P, Q, R), dấu của véc-tơ pháp tuyến, vùng chiếu D của bề mặt lên mặt phẳng tọa độ, và cuối cùng là tính tích phân hai lớp. Tài liệu cung cấp nhiều ví dụ minh họa từng bước để làm rõ cách áp dụng định nghĩa và các kỹ thuật tính toán khác nhau, kể cả khi bề mặt được cho dưới dạng phương trình z = f(x, y). Một điểm nhấn quan trọng là giới thiệu Công thức Ostrogradsky-Gauss (Định lý Gauss), một định lý mạnh mẽ cho phép chuyển đổi tích phân mặt trên một mặt kín thành tích phân ba lớp trên thể tích mà mặt đó bao quanh. Điều này không chỉ đơn giản hóa đáng kể quá trình tính toán trong nhiều trường hợp mà còn cung cấp cái nhìn sâu sắc về mối liên hệ giữa các đại lượng trên biên và trong miền. Các ví dụ áp dụng Định lý Gauss cũng được trình bày để minh họa hiệu quả của nó, cung cấp các công cụ thực tiễn để giải quyết các bài toán liên quan đến tích phân mặt loại II trong các ứng dụng khoa học và kỹ thuật.