Hàm số và tính chất
Đạo hàm và các ứng dụng
Tích phân và các ứng dụng
Dãy số và chuỗi số
Các quy tắc của đạo hàm
Đạo hàm hàm chuõi
Ý nghĩa hình học
Ứng dụng của đạo hàm
Chương 2
Đạo hàm
và
các ứng dụng
Giải tích 1: Hàm số một biến 37 / 136
Hàm số và tính chất
Đạo hàm và các ứng dụng
Tích phân và các ứng dụng
Dãy số và chuỗi số
Các quy tắc của đạo hàm
Đạo hàm hàm chuõi
Ý nghĩa hình học
Ứng dụng của đạo hàm
1.1 Định nghĩa đạo hàm
Đạo hàm của hàm số y=f(x)theo biến xlà hàm f′như sau
f′(x) = lim
h→0
f(x+h)−f(x)
h=df
dx =dy
dx =y′.(13)
Ví dụ: Tìm đạo hàm của f(x) = √x+2.
f′(x) = lim
h→0
(√x+h+2)−(√x+2)
h
= lim
h→0
√x+h−√x
h
= lim
h→0
1
√x+h+√x=1
2√x.
Giải tích 1: Hàm số một biến 38 / 136
Hàm số và tính chất
Đạo hàm và các ứng dụng
Tích phân và các ứng dụng
Dãy số và chuỗi số
Các quy tắc của đạo hàm
Đạo hàm hàm chuõi
Ý nghĩa hình học
Ứng dụng của đạo hàm
1.1 Định nghĩa đạo hàm
Hàm số f(x)có đạo hàm tại xnếu và chỉ nếu nó có đạo hàm bên
trái và đạo hàm bên phải và các đạo hàm này bằng nhau:
lim
h→0−
f(x+h)−f(x)
h= lim
h→0+
f(x+h)−f(x)
h=f′(x)(14)
Hàm số f(x)được gọi là khả vi trên một miền mở nếu nó có đạo
hàm tại tất cả các điểm trong miền này.
Hàm số f(x)khả vi trên một miền đóng [a,b]nếu nó khả vi trên
miền mở (a,b)và có đạo hàm bên phải tại điểm biên trái và có đạo
hàm bên trái tại điểm biên phải.
Nếu fcó đạo hàm tại x, thì nó liên tục tại x.
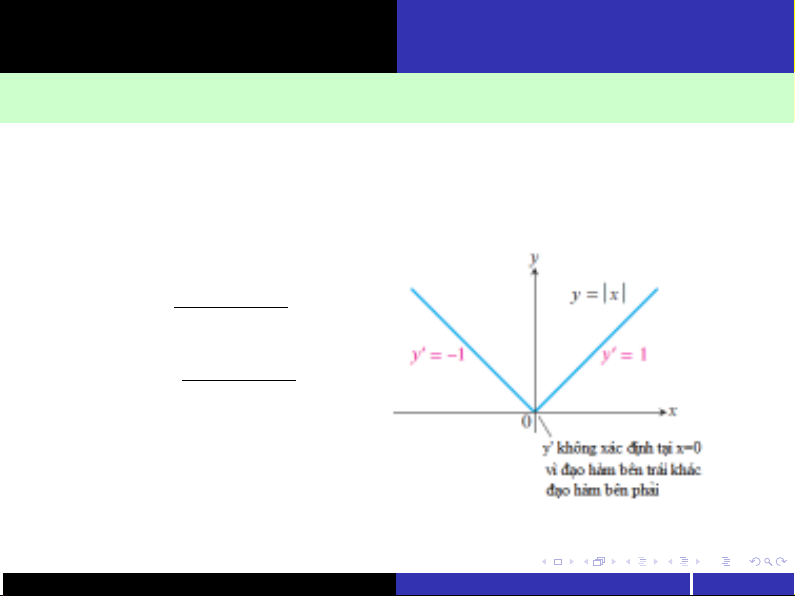
Nếu fliên tục tại x, nó có đạo hàm tại xkhông?
Giải tích 1: Hàm số một biến 39 / 136
Hàm số và tính chất
Đạo hàm và các ứng dụng
Tích phân và các ứng dụng
Dãy số và chuỗi số
Các quy tắc của đạo hàm
Đạo hàm hàm chuõi
Ý nghĩa hình học
Ứng dụng của đạo hàm
1.1 Định nghĩa đạo hàm
Ví dụ: Chứng minh rằng f(x) = |x|không có đạo hàm tại x=0.
Ta có
f′
−(0) = lim
h→0−
|0+h| − |0|
h=−1,
f′
+(0) = lim
h→0+|0+h| − |0|
h=1.
Do f′
−(0)6=f′
+(0)nên f(x)
không có đạo hàm tại x=0.
Giải tích 1: Hàm số một biến 40 / 136
Hàm số và tính chất
Đạo hàm và các ứng dụng
Tích phân và các ứng dụng
Dãy số và chuỗi số
Các quy tắc của đạo hàm
Đạo hàm hàm chuõi
Ý nghĩa hình học
Ứng dụng của đạo hàm
1.1 Định nghĩa đạo hàm
Bài tập: Dùng định nghĩa để tính các đạo hàm sau
1) f(x) = x2+1 tại x=1. 2) f(x) = 1
x−1tại x=2.
3) f(x) = √x+3 tại x=1. 4) f(x) = sin xtại x=π.
Bài tập: Các hàm số sau đây có khả vi hay không?
5) y=x,x<0,
−x,x≥0.6) y=x,x≤1,
−x2+2x,x>1.
7) y=(x,x≤0,
1
x,x>0.8) y=(x2sin 1
x,x6=0,
0,x=0.
Giải tích 1: Hàm số một biến 41 / 136