Bài gi ngả
Biên so n: TS. Ph m Văn S n ơ ạ ạ
B môn hình h a – V K Thu t ậ ẽ ỹ ộ ọ
Tr ườ ng ĐHBK Hà N i ộ
Ch
ng 1
ươ
phé p c hi uế
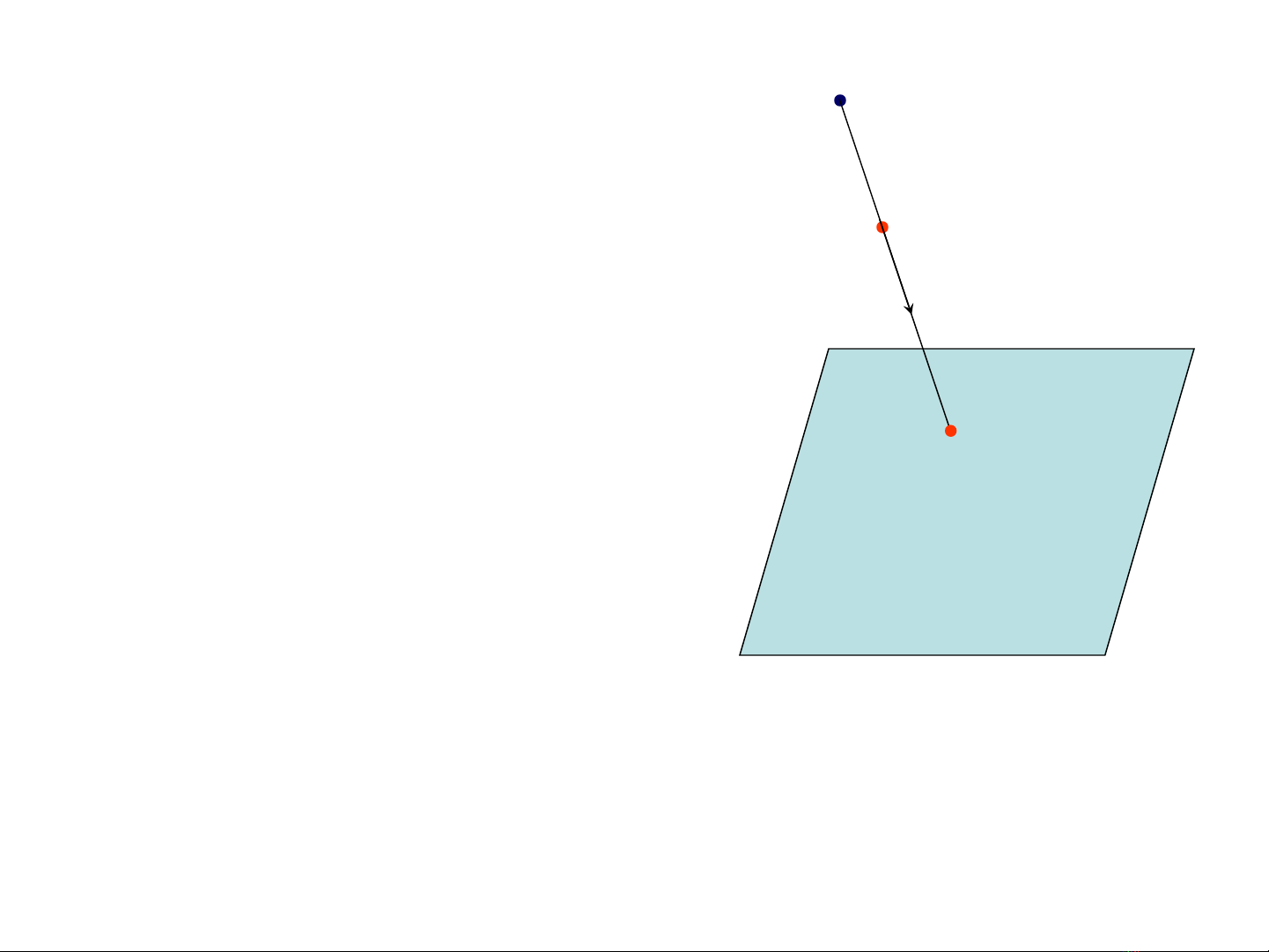
I. Phép chi u xuyên tâm ế
S
A Cho mặt phẳng Πi, gọi là mặt phẳng hình chiếu
Một điểm S không thuộc mặt phẳng Πi g i là tâm chi u ế ọ
Ai Chiếu một điểm A từ tâm S lên mặt phẳng Πi là :
1) Vẽ đường thẳng SA
Πi
2) Giao điểm của đường thẳng SA với mặt phẳng Πi là Ai
i là hình chi u xuyê n tâm c a đi m
Đi m Aể ể A ủ ế
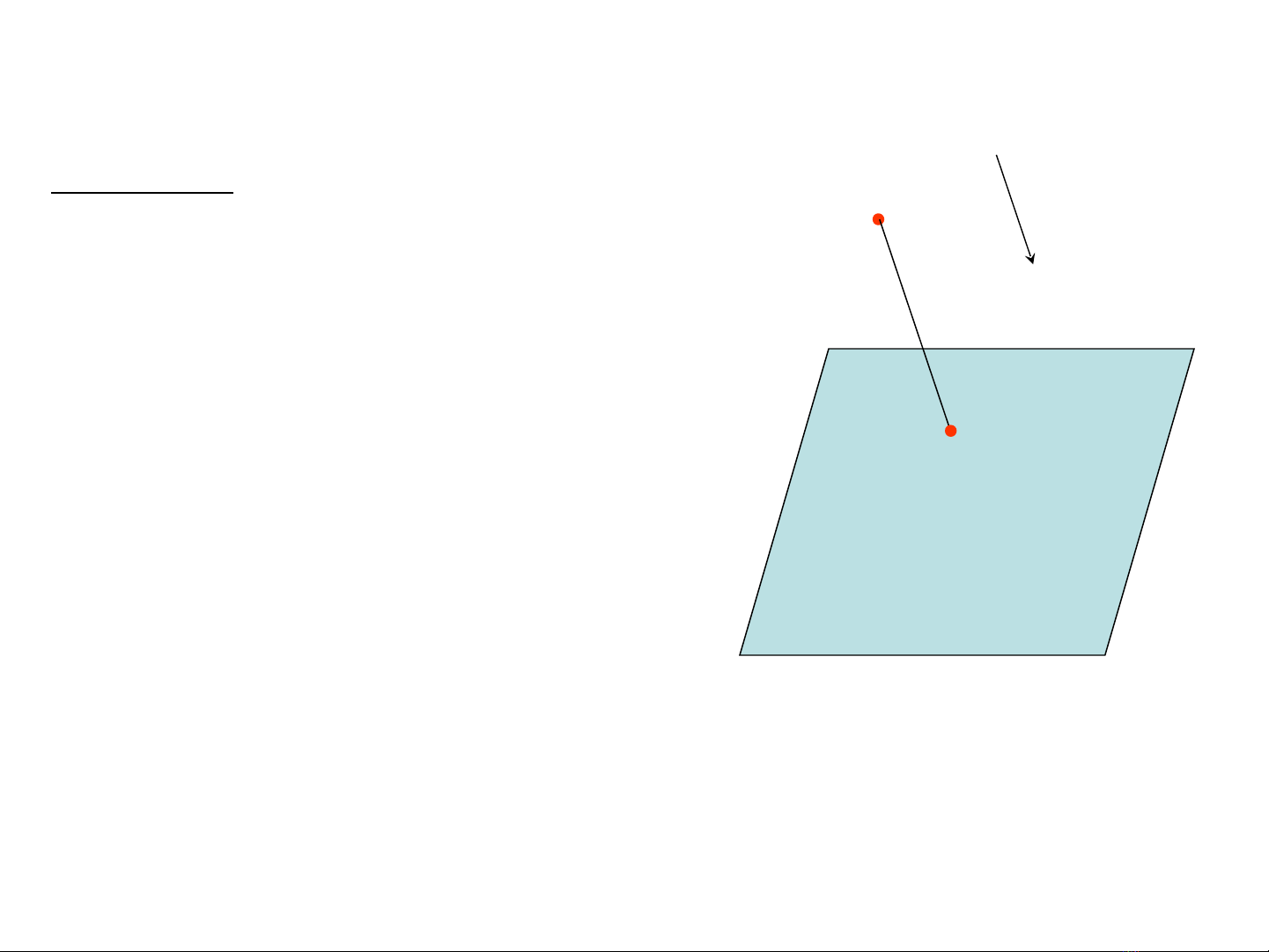
II. Phép chiếu song song
Đ nh nghĩa: ị
s A
d Cho mặt phẳng Πi, gọi là mặt phẳng hình chiếu
Ai Một đường thẳng s không song song với mặt phẳng Πi gọi là hướng chiếu
Chiếu một điểm A theo hướng s lên mặt phẳng Πi là:
Πi
1) Qua A vẽ đường thẳng d//s
2) Vẽ giao điểm của đường thẳng d với mặt phẳng Πi là Ai
i là hình chi u s ong s ong c a đi m A
Đi m Aể ủ ế ể
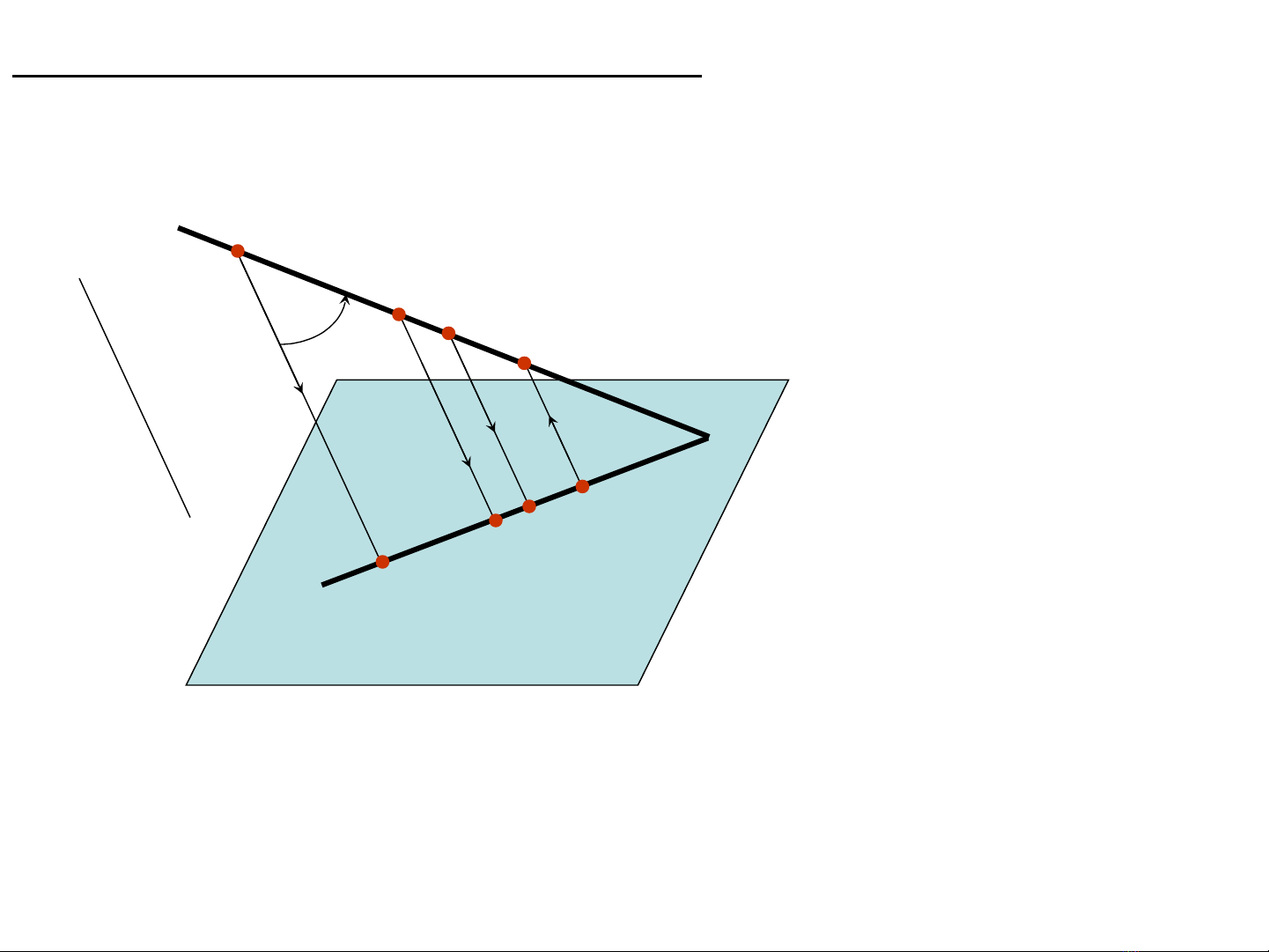
Tính ch t c a phé p chi u s ong s ong
ấ ủ
ế
1. Hình chiếu của một đường thẳng không song song với hướng chiếu là một đường thẳng A
a M a B N s
d e
N i ai Bi Mi Có thể xác định ai như sau
Ai
Πi
* Bước 1: Lấy 2 điểm A, B˛ a * b.2: tìm Ai, Bi theo định nghĩa
* b.3: Nối AiBi ta được ai
Chú ý: ai cũng là giao tuyến của mặt phẳng α với mặt phẳng Πi
ng h p đ c bi t 1 ườ ặ ợ ệ : Hình chiếu của một đường thẳng song
Tr song với hướng chiếu là một điểm
a
M
s
ai LMi
Πi
ng h p đ c bi t 2: ườ Một đường thẳng song song với mặt ệ ặ ợ
Tr phẳng hình chiếu thì song song với hình chiếu của nó
B a
A
α
s
ai
Bi
b Ai
Πi
Vµ AB=AiBi
ở ộ : một hình phẳng song song với mặt phẳng hình chiếu
M r ng thì có hình chiếu bằng hình thật
Πi
2. Hai đường thẳng song song (và không song song với hướng chiếu) thì hai hình chiếu song song.
A
a B k C
t b D s
ki
Bi
Ai ti Di
Ci
=
AB
:
CD
: DCBA i i
i
i
Πi
Vµ:
3. Phép chiếu song song bảo toàn thứ tự và tỷ số đơn của 3 điểm thẳng hàng
A
B
C
s
C i
Bi
A i
Πi
AB:BC=A iBi:BiC i
ng chi u thì hình chi u c a nó ộ ặ ớ ướ ế ủ ế
ng th ng 4. M t m t ph ng song song v i h ẳ suy bi n là m t đ ộ ườ ế ẳ
α
s M
gLαi
Mi
Πi
5. Một điểm nằm trên mặt phẳng hình chiếu thì điểm đó trùng với hình chiếu của nó.
s
A=Ai
Πi
III. Phép chiếu vuông góc
s
A
Cho mặt phẳng Πi, gọi là mặt phẳng hình chiếu
d
Chiếu vuông góc một điểm A lên mặt phẳng Πi là:
1) Qua A vẽ đường thẳng d vuông góc với mặt phẳng Πi Ai
Πi
2) Vẽ giao điểm của đường thẳng với mặt phẳng Πi là Ai
§iÓm A i lµ h×nh chiÕu vu«ng gãc cña ®iÓm A
1.5. Tính chất của phép chiếu vuông góc
ấ ủ ủ ế
* Có đ y đ các tính ch t c a phé p chi u s ong s ong, ngoài ra còn có các ầ tính ch t riê ng. ấ A
Tính ch t 1ấ
B
A i Bi
Hình chiếu của một đường thẳng không vuông góc với mặt phẳng hình chiếu là một đường thẳng Πi
t: Đ c bi ặ ệ
+ AiB iAB là hình thang vuông
+ AiB i Trê ng hîp ®Æ c biÖt 1 A B Hình chiếu
của một
đường thẳng
vuông góc với
mặt phẳng
hình chiếu là
một điểm Ai=Bi Πi Trê ng hîp ®Æ c biÖt 2 A B Một đường
thẳng song song
với mặt phẳng
hình chiếu thì
song song với
hình chiếu của
nó Ai Bi Πi ữ Chú ý: ABA iBi là hình ch nh t
ậ Hai đường thẳng song song (và không vuông góc với mặt phẳng hình
chiếu) thì hai hình chiếu song song. A Tính ch t 2ấ C B D Ai Bi Di C i Πi Phép chiếu vuông góc bảo toàn thứ tự và tỷ số đơn của 3 điểm thẳng
hàng A C Tính ch t 3ấ B A i C i Bi Πi AB:BC=A iBi:B iC i ộ ặ ủ ế ế ặ ẳ ẳ ng th ng M t m t ph ng vuông góc v i m t ph ng hình chi u thì hình chi u c a
nó s uy bi n là m t đ
ế ộ ườ ớ
ẳ Tính ch t 4ấ α M gLαi Mi Πi Một điểm nằm trên mặt phẳng hình chiếu thì điểm đó trùng với hình
chiếu của nó. Tính ch t 5ấ A=Ai Πi Tính ch t b o toàn góc vuông c a phé p chi u vuông góc: ấ ả ủ ế * Hình chiếu của một góc vuông nói chung không phải là một góc vuông; * Hình chiếu của một góc vuông là một góc vuông chỉ khi cóít nhất một
cạnh góc vuông song song với mặt phẳng hình chiếu và cạnh kia không
vuông góc với mặt phẳng hình chiếu. C A B AiBi AB^ BC ; AB//Πi;
BC^ Πi
fi ^ BiC i Bi TÝ nh chÊt 4 Ai C i Πi a b ^ (cid:252) M r ng:
ở ộ (cid:239) a // a
i b
i i ^ P (cid:253) b i (cid:239) P ^ (cid:254) b
i ^ (cid:252) a b ^ (cid:253) a
i
a // i P (cid:254) b a b
i a
i ^ (cid:252) ộ ạ (cid:253) ít nh t có m t c nh s ong
ấ
s ong v i ớ Πi ^ (cid:254) Tính ch t 4ấ Tính ph n chuy n c a hình bi u di n: ủ ễ ể ể ả i c duy nh t m t đi m A + V i m t đi m A, tìm đ
ể ộ ớ ượ ể ấ ộ ủ ể ế c A + Cho A i là hình chi u vuông góc c a đi m A, ta không
xác đ nh đ
ị ượ i là không có ậ ế ễ ằ ộ V y bi u di n đi m A b ng m t hình chi u A
ể
tính ph n chuy n. ể
ả ể A s d Ai Ai Πi Πi 2.1. Đồ thức của điểm trong hệ thống hai mặt phẳng hình chiếu ứ ế ặ ẳ ọ Π1 G i là m t ph ng hình chi u đ ng Π1 II x I III IV Π2 ế ằ ặ ọ Π2 G i là m t phăng hình chi u b ng ọ ế ằ ộ ng đ i c a A s o v i
ị ố ằ ấ ứ
ươ
phía d
ươ ộ Π1 A1 A Ax x A2 Π2 A1 G i là hình chi u đ ng,
ế
Đ cao c a A: V trí t
ị
ủ
có d u âm khi A
ở
Đ xa c a A: V trí t
ị
ủ
có d u âm khi A phía s au ng đ i c a A s o v i
ị ố ằ ấ ở A2 G i là hình chi u b ng
phía trê n
ớ Π2; có d u(+) khi A
Π2;
ở
ấ
=
=
z
AA
AA
A đ n
ướ Π2. Có tr s b ng kho ng cách t
ế Π2.
ả
ừ
2
1
A
x
ướ Π1;
c
phía tr
ớ Π1; có d u(+) khi A
ở
ấ
=
=
y
AA
AA
A đ n
ế Π1.
ừ
ả
1
2
x
A ọ
ố ủ
i
ố ủ
Π1. Có tr s b ng kho ng cách t Π1 A1 Ax x A2 Π2 Π1 A1 Ax x A2 Π2 Đồ thức của điểm trong hệ thống hai mặt phẳng hình chiếu Π1 A1 Ax x A2 Π2 Tính c h t:ấ ^ x 1) A1A2 2) Tồn tại duy nhất 1 điểm A A1 Ax x A2 Chú ý: A1Ax=Trị số độ cao của điểm A; A2Ax =Trị số độ xa của điểm
A Tính phản chuyển Π1 A1 Ax x A2 Π2 Π1 A1 Ax x A2 Π2 Π1 A1 Ax x A2 Π2 Π1 A1 A Ax x A2 Π2 2.2. Đồ thức của điểm trong hệ thống ba mặt phẳng hình chiếu Π1 Π z x 3 O Π2 y A1 là hình chiếu đứng A2 là hình chiếu bằng Π1 A3 là hình chiếu cạnh z
Az A1 Π x 3 A A3 Ax Ay A2 Π2 y Π1 Nh n xé t: ậ z
Az A1 * A1AzA3AAxOAyA2
là hình hộp chữ
nhật
fi AxA2=AzA3 Π x 3 A A3 Ax O Ay A2 Π2 y Π1 Π z
Az A1 x 3 A3 Ax O Ay A2 Π2 y Π1 Π z
Az A1 x 3 A3 Ax O A2 Ay y Π1 Π z
Az A1 x 3 A3 Ax O Ay A2 y Π1 Π z
Az A1 x 3 A3 Ax O A2 Ay y Π1=Π2 Π z
Az A1 x 3 A3 Ax O Ay A2 y Π1=Π2 Π 3 z
Az A1 A3 x Ax O A2 Ay
y Π1=Π2 Π3 z
Az A1 A3 x Ax O Ay A2 y Đồ thức của điểm trong hệ thống ba mặt phẳng hình chiếu Π1=Π2=Π3 z
Az A1 A3 x Ax O Ay A2 y Tính ch t:ấ ^ x A1A2 ^ z A1A3 z A2Ax=A3Az Az A1 A3 x Ax O A2 Biết hai hình chiếu, vẽ hình chiếu thứ ba z Az A1 A3 x Ax O A2 Biết hai hình chiếu, vẽ hình chiếu thứ ba z A3 A1 Az Ax x A2 O Biết hai hình chiếu, vẽ hình chiếu thứ ba z Az A1 A3 x Ax O A2 3.1. Biểu diễn đường thẳng trên đồ thức Có hai cách 1) Bi u di n b ng cách xác đ nh 2 đi m ể ễ ể ằ ị ế ằ 2) Bi u di n b ng cách cho 2 hình chi u( Không cùng vuông góc
ễ
ể
v i tr c x)
ớ ụ 3.1.1. Biểu diễn bằng cách xác định hai điểm B1 A1 x Ax Bx A2 B2 i tính ch t phé p chi u (Hình chi u c a m t đ ng ộ ườ ủ ế ế ấ Nh c l
ắ ạ
th ng):
ẳ A B A i Bi Πi 1B1là hình chi u đ ng c a AB; A 2B2 là hình chi u b ng ụ ứ ủ ế ế ằ áp d ng, ta có A
c a AB ủ B1 A1 x Ax Bx A2 B2 Một ví dụ khác về biểu diển đường thẳng qua hai điểm B1 x A1
Ax Bx A2 B2 Π1 B1 x A1 Ax Bx Π2 A2 B2 Π1 B1 x A1 Ax Bx Π2 A2 B2 Π1 B1 x A1 Ax Bx A2 Π2 B2 Π1 B1 x A1 Ax Bx A2 Π2 B2 Đường thẳng AB được gọi là đưong cạnh Π1 B1 A1 Π B 3 x A Bx= Ax A2 Π2 B2 3.1.2. Biểu diễn bằng cách xác định hình chiếu( không cùng vuông góc với
trục x) a1 x a2 Π1 x a1 Π2 a2 Π1 x a1 Π2 a2 Π1 x a1 Π2 a2 Π1 x a1 Π2 a2 Π1 α a1 x a Π2 β a2 Π1 Nếu cho hai hình chiếu cùng vuông góc với x, sẽ không
xác định duy nhất a: x a1 Π2 a2 Π1 x a1 Π2 a2 Π1 x a1 Π2 a2 Π1 a: bất kỳ thuộc mặt phẳng α L β α a1 Π 3 x a Π2 a2 β 3.2. Điều kiện điểm thuộc đường thẳng 3.2.1. Đ i v i đ ng ố ớ ườ ng th ng th
ẳ ườ ầ ộ I1 Đi u ki n c n và đ
ủ
ệ
đ đi m I thu c
đ a1 ng th ng a là:
ẳ
^ x.
˛ a2; I1I2 ề
ể ể
ườ
˛ a1; I2
I1 x a2 I2 ^ z Chó ý: I3 ˛ a3; I1I3 Thí d áp d ng: Cho đi m I thu c đ ng th ng a. Bi t I ụ ụ ể ộ ườ ẳ ế 1, tìm I2 I1 a1 x a2 I2 Gi¶i: 1- Tõ I1 vÏ ®êng ®ãng ^ x
2- §êng dãng trªn c¾t a2 lµ ®iÓm I2
cÇn t×m 3.2.1. Đ i v i đ ng th ng c nh ố ớ ườ ạ ẳ Thường áp dụng hai mệnh đề sau: Đi u ki n c n và đ đ đi m M thu c
ộ ủ ể ể ệ ề ầ Đ ng th ng AB là
ả ^ z ườ
˛ A1B1; M3 M1 ˛ A3B3 và M1M3 Hoặc: Đi u ki n c n và đ đ đi m M thu c
ộ ủ ể ể ệ ề ầ Đ ng th ng AB là:
ẳ ườ
˛ A1B1; M2 M1 ˛ A2B2 và tỷ số đơn (A1,B1,C1)=(A2,B2,C2) 1, ng th ng AB. Bi t M ụ ể ộ ườ ẳ ế Thí d áp d ng: Cho đi m M thu c đ
ụ
tìm M2 z B3 B1 M3 M1 A3 x A1
Ax Bx O A2 M1 B2 B1 B1 M1 M1 x x A1
Ax A1
Ax Bx Bx A' M' B' A2 A2 M' B' M2 M2 B2 B2 3.3. Độ lớn thật của một đoạn thẳng và góc của nó so
với các mặt phẳng hình chiếu ẳ ỏ ế
ẳ ạ
ủ ự ặ ớ Bài toán: Cho đo n th ng AB xác đihnh b i các hình chi u. Hãy
tìm đ dài th c c a AB và góc c a nó s o v i các m t ph ng
ủ
ộ
hình chi u. ế B1 Bx x A1
Ax A2 B2 Phân tích: Gi :ả B1 Đ ộ dà i A B B α yAB yAB D D α A E A1 Bx x Ax yAB A2 D A 1 B1 B2 Π1 yAB AA1: độ xa của A =A2Ax yAB làm BB1: độ xa cửa B =B2Bx yAB là hiệu độ xa A và D AA1B1B là hình thang
vuông
B 1- Lấy A1B1làm một cạnh của tam giác
2- Xác định D
vuông
3- Dùng 1 đường vuông góc với A1B1tại A1
hoặc B1, trên đó lấy 1 đoạn = D
cạnh thứ hai của tam giác vuông
4- Cạnh huyền của tam giác vuông này là độ
dài thật của AB. α là góc của AB so với Π1 Ph©n tÝ ch: Gi¶i: B1 B zAB zAB D D β A E Bx x A1
Ax A2 zAB D A 2 B2 β ĐDTAB B2 Π2 zAB AA2: (độ cao của A)=A1Ax zAB làm BB2: (độ cao của B)=B1Bx zAB là hiệu độ cao A và D AA2B2B là hình thang
vuông
B 1- Lấy A2B2 làm mét cạnh của tam giác
2- Xác định D
vuông
3- Dùng 1 đường vuông góc với A2B2tại A2
hoặc B2, trên đó lấy 1 đoạn = D
cạnh thứ hai cửa tam giác vuông
4- Cạnh huyền của tam giác vuông này là độ
dài thật của AB. β là góc của AB so với Π2 3.4. Các đường thẳng có vị trí đặc biệt so với các mặt
phẳng hình chiếu Các đ ng th ng s ong s ong v i các m t ph ng hình chi u: ườ ế ẳ ẳ ặ ớ 1) Đường bằng: Là đường thẳng song song với mặt phẳng hình
chiếu bằng 1 B A1 h1 Π1 Ax x Bx 1 B A1 h1 2 A A2 h B h2 B P A2 2 B h2 Π2 2) Đường mặt: Là đường thẳng song song với mặt phẳng hình
chiếu đứng f1 B 1 f1 Π1 1 A1 B f P B A1 x A 2 B A2 f2 2 B f2 A2 Π2 2) Đường cạnh: Là đường thẳng song song với mặt phẳng hình
chiếu cạnh và có hình chiếu đứng, hình chiếu bằng cùng vuông
góc với x B1 x A1
Ax Bx A2 B2 Π1 B1 x A1 Ax Bx Π2 A2 B2 Π1 B1 x A1 Ax Bx Π2 A2 B2 Π1 B1 x A1 Ax Bx A2 Π2 B2 Π1 B1 x A1 Ax Bx A2 Π2 B2 Đường thẳng AB được gọi là đường cạnh Π1 B1 A1 Π 3 x B B3 A A3 Bx= Ax A2 Π2 B2 Các đ ng th ng vuông góc v i các m t ph ng hình chi u: ườ ế ặ ẳ ẳ ớ 4) Đường thẳng chiếu đứng: là đường thẳng vuông góc với mặt
phẳng hình chiếu đứng A1=B1 Π1 x A1=B1 A A2 B A2 B2 B2 Π2 4) Đường thẳng chiếu bằng: là đường thẳng vuông góc với mặt
phẳng hình chiếu bằng A1 B1 Π1 A1 x A B1 B A2=B2 B2=A2 Π2 4) Đường thẳng hình chiếu cạnh: là đường thẳng vuông góc với
mặt phẳng hình chiếu cạnh. Π1 Π 3 B1 A1 B1 A1 x A3=B3 A B A2 B2 A2 B2 Π2 3.5. Vị trí tương đối của hai đường thẳng. Trong không gian, hai đường thẳng có thể: C t nhau ắ S ong s ong Ché o nhau n u không c t nhau và không s ong s ong
ắ ế 3.5.1 trường hợp cả hai đường không phải là đường
cạnh. ng th ng c t nhau ườ ẳ ắ a) Hai đ
nhau: M1 b1 · (cid:236) a1 (cid:239) =
Mba a
1
a 2 · (cid:219) · (cid:237) x =
Mb
1
1
=
Mb
2
2
xMM
2 1 b2 (cid:239) ^ a2 (cid:238) M2 t: Đ c bi
ặ ệ M1 M1 b1 a1=b1 a1 x x b2 a2 a2=b2 M2 M2 ng th ng s ong ườ ẳ b) Hai đ
s ong: a1 // b1 (cid:236) ba
// a
1
a // (cid:219) (cid:237) x 2 b
1
b
2 (cid:238) b2 a2 t: Đ c bi
ặ ệ a1=b1 a1 b1 x x b2 a2 a2=b2 ng th ng ché o ườ ẳ c) Hai đ
nhau: M1 b1 b1 a1 a1 x x b2 b2 a2 a2 M2 3.5.2 trường hợp một trong hai đường là đường cạnh ng th ng này không s ong s ong cho c t nhau ho c ậ ườ ẳ ắ ặ Nh n xé t: Hai đ
ché o nhau C1 B1 A1 D1 A2 D2 B2 C2(?) a) Cắt nhau C3 C1 C1 B1 B1 I1 I1 B3 A3 I3 A1 A1 D1 D1 D3 A2 A2 I' D2 D2 C
' B2 B2 I2 C2 C2 C¸ch 2 C¸ch 1 C1 B1 A1 D1 A2 D2 B2 C2 C¸ch 3 a)Chéo nhau: ng h p này, hai đ ng th ng không c t nhau thì ợ ườ ẳ ắ Trong tr
ườ
ché o nhau 3.5.2 Trường hợp cả hai đường là đường cạnh A1 A1 C1 C1 B1 B1 D1 D1 x x A2 A2 C2 C2 B2 B2 D2(?) D2(?) Lo¹i 2: Song song hoặc cắt nhau Loại 1: Song song hoặc chéo
nhau Lọai 1: S ong s ong: A1 A1 A3 C1 C1 C3 I1 B3 B1 B1 D1 D1 D3 x x A2 A2 C2 C2 I2 B2 B2 D2 D2 Trong trê ng hîp nµy 2 ®ê ng kh«ng s ong s ong th× chÐo nhau ng th ng c t nhau, ọ ế ế ắ ạ ườ ẳ ắ L ai 2: N u hình chi u c nh c t nhau thì hai đ
hình chi u c nh s ong s ong thì hai đ ng s ong s ong. ườ ế ạ C1 B1 D1 x A2 C2 B2 D2(?) 3.5. Vết của đường thẳng
Đường thẳng a cắt tại điểm M, thì điểm M được gọi là vết đứng của đường
thẳng a Π1 Đường thẳng a cắt tại điểm N, thì điểm N được gọi là vết bằng của đường
thẳng a M1 M a1 M1 a1 N1 a N1 x M2 x M2 a2 a2 N =N2 Π2 N2 (II) (I) (IV) Bµi to¸n : VÏ giao ®iÓm cña ®êng th¼ng vµ c¸c mÆt ph¼ng h×nh chiÕu. XÐt xem
®êng th¼ng ®ã ®i qua c¸c gãc phÇn t nµo z M3 M1 A3 Π1 A1 M M3 M1 Π 3 B3 A1 B1 A A3 x M2 =N1 N3 B1 x A2 M2 N1= A2 B B3 B2 B2 N3 Π2 N N2 N2 Biểu diễn trên đồ thức B1 M1 c1 N1 a1 b1 A1 x a2 b2 C1 c2 x M2 N2 C2 α(a//b) A2 α(aGc) α(ABC) B2 c1 a1 M1 M1 a1 b1 x x a2 a2 M2 b2
M2 c2 α(a,M) α(aGb) α(a//c) IIĐiều kiện điểm, đường thẳng thuộc mặt phẳng Mệnh đề 2 M nh đ 1: :Mệnh đề 3: ệ ề M M a a a b N M α α α α Cho m t ph ng
ặ ẳ Cho m t ph ng
ặ Cho m t ph ng
ặ ẳ Đi m M ˛ α và N ˛ α ể Đ ng th ng a ẳ α
˛ α Đ ng th ng a α
˛ α ườ ẳ ườ ẳ ẽ ườ ng th ng a
ẳ Đi m M ˛ a thì M˛ α ể ể Qua M và N v đ
thì a˛ α ng ˛ α
ẽ ộ ườ Đi m M
Qua M v m t đ
˛ α
th ng b//a thì b ẳ ề
ặ ể ng th ng
ẳ Đi u ki n đi m thu c
ộ
ể
ệ
m t ph ng là đi m n m
ằ
ẳ
trên m t đ
ng th ng
ộ ườ
ẳ
c a m t ph ng
ẳ
ặ
ủ ề
ộ ể Đi u ki n đ
ệ ườ
ề
thu c m t ph ng là
ẳ
ặ
ộ
ng th ng đi qua 2
đ
ườ
ẳ
đi m c a m t ph ng
ặ
ể ủ ẳ ẳ ặ Đi u ki n đ
ng th ng
ệ ườ
ẳ
ng
thu c m t ph ng là đ
ườ
ẳ
ặ
th g đi qua 1 đi m c a m t
ẳ
ủ
ặ
ph ng và song song v i m t
ẳ
ộ
ớ
đ
ng th ng c a m t
ủ
ườ
ph ngẳ Thí d áp d ng: ụ ụ ng ườ B1 B1 M1 M1 g1 g1
N1 A1 A1 C1 C1 x x C2 C2 A2 A2 g2 M2 g2 M2 N2 B2 B2 Cho m t ph ng
ẳ
ặ
˛ α. Bi
th ng g
ẳ α(ABC), đ
t gế 1, tìm g2 . α(a//b), đi m M ể α(ABC), đi m M ể a1 B1 b1 M1 g1 M1 D1 A1 x A2 b2 M2 g2 D2 M2 a2 B2 Cho m t ph ng
ặ
˛ α. Bi
t Mế ẳ
1, tìm M2 . Cho m t ph ng
ặ
˛ α. Bi
t Mế ẳ
1, tìm M2 . III.Các mặt phẳng có vị trí đặc biệt so với các mặt phẳng hình chiếu 1. M t ph ng chi u đ ng là m t ph ng vuông góc ế ứ ặ ẳ ặ ẳ v i m t ph ng hình chi u đ ng ẳ ặ ớ ế ứ Π1. Π1 M1 α1 g1= α t1 M1 t1 x M α1 g1= g t M˛ α g˛ α Π2 t˛ α ặ ế ế ặ ẳ ằ ẳ ằ ặ ẳ ớ 2. M t ph ng chi u b ng là m t ph ng vuông góc v i m t ph ng hình chi u b ng
Π2. Π1 α x t M M2 g t2 α2 g2= M˛ α M2 α2 t2
g2= g˛ α Π2 t˛ α 3. M t ph ng b ng là m t ph ng song song ẳ ằ ặ ặ ẳ v i m t ph ng hình chi u b ng ế ẳ ặ ớ ằ Π2. A1 B1 C1 Π1 α1 α1 x B2 A2 α C2 Π2 4. M t ph ng m t là m t ph ng song song ặ ẳ ặ ặ ẳ v i m t ph ng hình chi u đ ng ẳ ặ ớ ế ứ Π1. C1 α Π1 A1 B1 x α2 α2 A2 B2 C2 Π2 IV.Vết của mặt phẳng ặ ườ α c t ắ Π1 the o đ 1. V t c a m t ph ng ng th ng đó g i là ế ủ ẳ ặ ẳ ng
ọ M t ph ng
ẳ
α thì đ
th ng mẳ
v t đ ng c a
ế ứ ườ
ư α; ườ ng th ng đó g i là ẳ ng
ọ Π1 M t ph ng
ặ
ẳ
th ng n
α thì đ
ẳ
v t b ng c a
ế ằ α c t ắ Π2 the o đ
ườ
ủ α. α α m m1 n
α αx m2=n1 x Nh n xét: ậ n2 Π2 mαGnα=αx trên trục x m1 = mα ; m2=x n2 = nα ; n1 =x 2a Cách v v t c a m t ph ng ẽ ế ủ ặ ẳ m1 31 α m b1 a1 Π1 3 a αx 21 x αx 32 11 x m2 =n1 n
α a2 1 b 22 2 Π2 b2 n2 12 V đ ng b ng c a m t ph ng ẽ ườ ủ ằ ẳ ặ B1 m1 A1 C1 D1 h1 I1 x C2 A2 x I2 αx m2=n1 h2 D2 B1 n2 Trong mét mÆt ph¼ng, c¸c ®êng b»ng song song víi nhau vµ song
song víi vÕt b»ng. V đ ng m t c a m t ph ng ẽ ườ ặ ủ ặ ẳ B1 m1 A1 f1 x A2 D1
C1 x αx I1 m2=n1 C2
D2 f2 I2 B1 n2 Trong mét mÆt ph¼ng, c¸c ®êng mÆt song song víi nhau vµ song
song víi vÕt ®øng. 2b Cách v v t c a m t ph ng ẽ ế ủ ẳ ặ m1 f1 h1 11 αx m2=n1 f2 12 h2 n2 V.Giao của đường thẳng với mặt phẳng. Giao của hai mặt
phẳng
1. Tr
ườ ng h p đ c bi t
ệ ợ B1 ặ
t1 A1 M1 α1 =g1 C1 C2 A2 α1 g2 B1 t2 M2 α . ủ ể α Gi
ả ử
V y M là giao đi m c a t và
ậ s M là giao đi m c a t và
ể ủ s g là giao tuyÕn c a g=αGβ(ABC) ủ α vµ Gi
ả ử
β(ABC). ˛ ˛ ˛ ^ x. tfi V y Mậ t1; M2 t2; M1M2 ˛ αfi g1=α1. ˛ M1
Và M˛ α fi M1 α1 1=t1 G α1.
T đó Mừ
Dóng v tề 2 ta có M2. c g
ẽ ượ 2
g˛ β, bi ˛ β. Ta v đ
i bài toán
ả t ế V y gậ
M t khác g
ặ
b ng cách gi
ằ
g1 tìm g2. α1 α1 =g1 g1 β1 g2 =g2 β2 s g là giao tuy n c a ế ủ α và s g là giao tuy n c a ế ủ α và Gi
ả ử
β(ABC). Gi
ả ử
β(ABC). V y g ậ V y gậ ˛ αfi g1=α1. ˛ αfi g1
Và g˛ βfi g1 ˛ α1.
˛ β1. M t khác g ặ ˛ βfi g2 =β2. 1 là 1 đi mể
^ x (cid:222) V y gậ
g2 ẽ ng th ng
ẳ a1 ủ ườ
α V giao đi m c a đ
t và m t ph ng
ặ ể
ẳ S1 A1 b1 M1 A1 B2 C1 x B2 C2 A2 A2 =M1
t1 t1 b2 M2 =M2 t2 S1 t2 a2 Gi s M là giao đi m c a t và α ả ử ủ ể Gi s M là giao đi m c a t và α ả ử ủ ể fi M˛ α và M˛ t. fi M˛ α và M˛ t. ˛ ˛ V i đi u ki n M ề ớ V i đi u ki n M ề ớ 2 ta s ẽ tìm 1 ta s ẽ tìm ệ
˛ α, nên bi t (cid:222) M2Lt2
t Mế ệ
˛ α, nên bi 1 2 t (cid:222) M1Lt1
t Mế M t khác M
ặ
c Mượ
đ M t khác M
ặ
c Mượ
đ ng pháp m t ph ng ph tr gi i bài toán giao c a đ ụ ợ ả ẳ ặ ủ ườ ng th ng v i m t
ặ ẳ ớ Ph
ươ
ph ng:ẳ B1 2. Tr ng h p t ng quát: ườ ợ ổ t t1 g1= M1 β1=
A1 β C1 x C2 A2 M g α g2 M2 B1 t2 ng t (th ng ườ ẽ ặ ườ ẽ ng th ng g)
ẳ
ủ
ể β ch a đ
1) V m t ph ng
ứ ườ
ẳ
l y ấ β là m t ph ng chi u)
ẳ
ế
ặ
ế ủ α và β (đ
2) V giao tuy n c a
3) Giao đi m c a t và g chính là giao đi m c a
ủ
ể
t và α ế ủ ặ ẳ B1 q (t//k) Bài toán: V giao tuy n c a m t ph ng
ẽ
α(ABC) và m t ph ng
ẳ ặ t1 g1= M1 β1=
A1 1 x =g =g'1 k1
N1 A2
g2 g'2 N2 M2 B1 t2 k2 Ph ng pháp m t ph ng ph tr gi ươ ụ ợ ả ặ ẳ i bài toán giao c a hai m t ph ng:
ủ ặ ẳ A α β k t g B t' k' q Thí d áp d ng ụ ụ 1 c1 d1 b1 g a1 =g1 =k1 M1 1 q =g'1=k'1 N1 k'2 M2 b2 g2 a2 N2 c2 g'2 k2 d2 V giao tuy n c a hai m t ph ng cho b ng v t
ế ế ủ ẽ ằ ẳ ặ m A =A1 Π1 β m β α m A α m B1 αx βx A2 β n
α n n
α nβ αx βx B =B2 B Π2 AB=αGβ V.Đường thẳng song song với mặt phẳng Hai mặ phẳng song song. 1. Đ ng th ng song song v i m t ph ng ườ ặ ẳ ẳ ớ ề ẳ ườ ng th ng
ẳ Đi u ki n đ m t đ
ẳ
này ph i song song v i m t đ
ộ ườ ể ộ ườ
ớ ng th ng song song v i m t m t ph ng là đ
ớ
ng th ng c a m t ph ng.
ủ ệ
ả ộ
ặ ặ
ẳ ẳ b a α b//a; a˛ α (cid:222) a//α ng th ng t đi qua M và song song t đ
ế ườ ẳ ẽ 2 bi α(ABC). Thí d áp d ng: V t
ụ
v i m t ph ng
ẳ
ớ ụ
ặ B1 t1 M1 A1 C1 B2 // A2 t2 M2 C2 V m t ph ng α(ABC) song song v i đ ẽ ặ ẳ ớ ườ ng th ng t.
ẳ B1 I1 t1 M1 A1 C1 B2 I2 A2 t2 M2 C2 1. Hai m t ph ng song song
ẳ ặ ể ẳ ẳ ủ ẳ ẳ ẳ
Điều kiện đ hai mặt ph ng song song là mặt ph ng này chứa 2 đường th ng cắt
nhau tương ứng song song với 2 đường th ng cắt nhau c a mặt ph ng kia a b α aGb=α;
cGd=β; (cid:222) α/β a//c;
b//d. c d β ẽ ặ ể ẳ β song song v i ớ Thí d áp d ng: Qua đi m M v m t ph ng
ụ
m t ph ng ụ
α(ABC) ặ ẳ t1 B1 M1 1 Qua M, v t//AB
2 Qua M, v k//AC ẽ
ẽ k1 ẽ ầ ẳ 3 M t ph ng c n v là
ặ
β(t,k) A1 C1 B2 t2 M2 A2 k2 C2 Qua đi m M v m t ph ng ẽ ặ ể ẳ β song song v i m t ph ng
ớ ặ ẳ α(mα,nα) m1 m'1 f1 h1 M1 αx x m'2=n'1 m2=n1 M2 f2 h2 n2 n'2 ẽ 1 Qua M, v h//n
2 Qua M, v f//mẽ 3 M t ph ng c n v là β(h,f) ẽ ẳ ầ ặ 4 V các v t c a ế ủ β ẽ VI.Đường thẳng vuông góc với mặt phẳng. M t s m nh đ c n chú ý: ộ ố ệ ề ầ ể ẳ ẳ ẳ
ẳ ẳ ủ ủ ẳ Mệnh đề 2: điều kiên đ một
đường th ng vuông góc với
một mặt ph ng là nó vuông
góc với hai đường th ng cắt
nhau c a mặt ph ng đó ẳ Mệnh đề 1: Nếu một đường
th ng vuông góc với một mặt
ph ng thì nó vuông góc với
ẳ
mọi đường th ng c a mặt
ph ng đó d d a t b α α b ^ (cid:252) a
a // a
i b
i i (cid:239) ^ P (cid:253) b i (cid:239) P ^ (cid:254) b
i ^ (cid:252) a b ^ (cid:253) a
i
a // i P (cid:254) i a
a
i b
b
i ^ (cid:252) ặ (cid:253) ít nh t a ho c b song
ấ
song v i ớ P ^ (cid:254) M t s bài toán c b n: ộ ố ơ ả ng th ng d, Qua đi m M hãy v m t ph ng α vuông góc ườ ẽ ặ ể ẳ ẳ Bài toán 1: Cho đ
v i dớ 2; d^ α (cid:222) α là mặt α qua d1 (cid:222) Phân tích: d//P
ẳ
ph ng chiếu bằng. Mặt khác đt
ể
cách vẽ
đi m M M1 ng th ng
ẳ d2 * Qua M2 v đ
ẽ ườ
vuông góc v i dớ 2 α2 M2 ng th ng d, Qua đi m M hãy v m t ph ng α vuông góc ườ ẽ ặ ể ẳ ẳ Bài toán 1: Cho đ
v i dớ f1 ẳ ủ ẳ α. Chọn 2 M1 h1 d1 2 suy ra ặ ị d2 1 suy ra f2 f Mặt khác h//P ^ cách vẽ f M2 Phân tích: điều kiện d^ α là d ph i ả
vuông góc với hai đường th ng cắt
nhau c a mặt ph ng
đường đó lần lượt là đường bằng h
và đường mặt f.
d^ α (cid:222) d^ h MÆt kh¸c h//P
α xác đ nh b i h và f là m t
M t ph ng
ở
ẳ
ặ
ph ng c n v .
ẽ
ầ
ẳ
^ h2 (cid:222)
c¸ch vÏ h
d2
d^ α (cid:222) d^
f1 (cid:222)
d2 h2 ể ẳ Bài toán 2: Cho mặt ph ng ẳ α, Qua đi m M hãy vẽ đường th ng d vuông góc với mặt
ph ng ẳ α. f1 m1 d1 M1 d1 h1 αx x m2=n1 f2 d2 M2 2 suy ra h2 n2 d2 1 suy ra f Mặt khác h//P ^ d^ α (cid:222) d^ h Mặt khác h//P
^ h2 (cid:222)
cách vẽ d2
d2
d^ α (cid:222) d^
f1 (cid:222)
d2 cách vẽ d1 ể ẳ Bài toán 2: Cho mặt ph ng ẳ α, Qua đi m M hãy vẽ đường th ng d vuông góc với mặt
ph ng ẳ α. B1 M1 ư ề ộ d1 f1 h1 ả ở ụ A1 1 đ a v m t trong 2
d ng trên
ạ
2 áp d ng k t qu
trên, ta v đ c d ế
ẽ ượ C1 A2 C2 f2 M2 h2 d2 B2 ể ẳ ả Thí dụ áp dụng: Tìm kho ng cách từ 1 đi m M đến một mặt ph ng a (m,n). H YAB § dt M 1 Qua M v dẽ ^ α(m,n) D m1 ể H c a d ủ M1 2 V giao đi m
ẽ
và α. d1 3 Tìm đ dài th t MH ậ ộ H1 αx x m2=n1 H2 YAB D d2 M2 n2 ệ c t o thành b i các đa giác
ở ượ ạ đa di n là m ăt kín đ
ph ng (l i) g n li n v i nhau b i các c nh c a chúng.
ớ ủ ề ẳ ạ ắ ồ ở D A S B C D A D’ A’ B B’ C C’ Trên đồ thức, đa diện được biểu diễn thông qua biểu diễn
các cạnh của chúng với qui định: các mặt của đa diện là
không trong suốt. S1 a1 b1 d1 c1 a1 S1 P1 a1 b1 c1 d1 + + - - - + M1=N1 + A1 A1 C1 A1 C1 B1 Q1 M1=N1 c2 M2= B1 A2 A2 N2 C2 + a2 B2 P2=Q2 S2 d2 - C2 S2 N2 B2 M2 +
A2 b2 Giao của một mặt phẳng với một đa diện là một đa giác
phẳng mà mọi đỉnh của nó là giao điểm của 1 cạnh đa diện
với mặt phẳng, mỗi cạnh của nó là giao của mặt phẳng với
một mặt của đa diện S F M D E N A C B M1 N1 Mặt phẳng chiếu
cắt đa diện P1 =Q1 P2 M2 Q2 N2 Q1
c1 a1 b1 Mặt phẳng cắt đa
diện là trụ chiếu m1 K1 P1 m2=n1 c2 =Q2 a2 K2= n2 b2 =P2 =d a1 1=t1 1=k1 =g
b1 F1 =b 1=g1 c1 D1 m1 E1 m2=n1 g2 k2 t2 n2 D2 c2 F2 a2 E2 b2 a1 b1 d1 M1=N1= A1 c1 B1 C1 C2 d2 c2 A2 M2 a2 N2 B2 b2 S1 d1 M1=N1= A1 B1 C1 C2 d2 A2 M2 N2 S2 B2 Trường hợp tổng quát S F R M D E V t N A C B S1 M1 N1 A1 P1 V1 R1 d1 1 B1 C1 C2 d2 A2 P2 M2 R2 S2 V2 N2 B2 =b a1 1
E1 M1 b1 V1 A1 N1 c1 B1 R1 P1 M’ C1 F’ P’ R’ V’ C2 E’ F1
F2
P2 A2 N’ R2 c2 M2 a2 V2 N2 B2 E2 b2 b S c a V F F R V E R t E t N b A Q C P N M B P Q M a1 E1 d1 1 b1 V1 M1 A1 P1 R1 B1 Q1 C1 F1 e1 N1
N2 e2 C2 F2 A2 R2 Q2 c2 P2 a2 V2 B2 M2 d2 E2 b2 b S1 e1 11 31 S2 e2 21 41 d1 f1 + 51=61 f2 2 B1 A1 C1 4 - 5 d2 6 + 22 1 C2 3 e2 12 A2 + A2 52
62 + + A2 C2 B2 S2
32 d2 e2 f2 42
B2 e1 S1 11=21 31=41 f2 g2 e2 e2 51 A2 + - 71 + A1=B1 61 f1
91=101 81 3 + g1 1 B2 C1 2 4 S2 + 10 5 D1 C2 6 7 - D2 8 1 9 82 D2 92 A2 72 + 3 32 12 A2 S2 B2 22 42 52 102 62 e2 g2 f2 C2 a1 e1 b2 g1 c2=d2 f1 g2 f2 e2 d2 a2 b2 c2 S1 11 31 A1 - + + + - 41 71 21 91 B1
5(eh) - e1 f1 111
g1 S1 h1 2 1 51 81 61 6(hg)
C1 C1 A1 121 B1 D1 101 11 3 + 7 h2 4 9 S2=B2 D1 + 12 =52 e1 h1 f1 g1 h1 62= 22 e2 32
=72=82 C2 A1 A2 g2 =112=122 92=102= 42
f2 D2 S1 e1 11 21 A2 51 A1 C1 d1 31 41 f1 6 61=71 + 2 3 S2 B2 4(df) +
+ B1 7 52 C2 1 C2 A2 5(de) 42 + - 12 72
62 S2 e2 +
d2 e2 f2 d2 A2 22 32 d2 f2 e2 B2Ch
ng 2
ươ
§Đi mể
Ch
ng 3
ươ
Đ ng th ng
ườ
ẳ
Ch
ng 4
ươ
M t ph ng
ẳ
ặ
Ch
ng 5
ươ
ổ
c ác phé p bi n đ i hình
ế
c hi uế
Ch
ng 6
ươ
đa di nệ
đa diện
Chãp(th¸p)
L¨ng trô
§a diÖn bÊt kú
Bi u di n đa di n
ễ
ể
ệ
Giao m t ph ng v i đa di n
ẳ
ớ
ệ
ặ
P
S1
ng h p đ c
ợ
ặ
a1
Tr
bi
ườ
tệ
A1
C1
B1
C2
A2
S2
B2
Tr
ng h p
ườ
ợ
Đ c bi
ặ
t
ệ
ng h p
ợ
ườ
Tr
t ng quát
ổ
Giao c a đ
ng th ng và đa di n
ủ
ườ
ệ
ẳ
h p
ợ
ng
ườ
ệ
Tr
ng
bi
t: đ
ườ
c hi u c t đa di n
ắ
ế
đ c
ặ
th ng
ẳ
ệ
Giao c a đ
ng th ng và đa di n
ủ
ườ
ệ
ẳ
P
Giao c a hai đa di n
ủ
ệ
ệ
ủ
ườ
ề
ặ
ọ ỉ
ộ
ớ
ệ
ệ
ặ
ủ
ộ
ộ
ớ
ễ
ặ
ặ
ộ
ạ
ệ
ng g p
Giao c a hai đa di n là m t ho c nhi u đ
ấ
ộ
khúc khô ng g ian khé p kín mà m i đ nh là g iao đi m c a
ủ
ể
m t c ahnh đa di n này v i m t m t đa di n kia; m i
ỗ
c nh là g iao c a m t m t đa di n này v i m t m t đa
di n kia.
Các h v g iao tuy n:
ẽ
ế
ầ ượ
ủ ừ
ớ
c l
ượ ạ
ượ
ủ
+ L n l
t tìm g iao c a t ng c nh đa diê n này v i c ác
ạ
c c ác đ nh c a
i, ta đ
m t đa di n kia và ng
ỉ
ệ
ặ
g iao tuy n.ế
ỉ
ế
ượ
ộ
ộ
ắ
ặ ủ
ạ
ủ
ố ớ
ừ
ệ
ộ
ả
ấ
+ N i c ác đ nh c a g iao tuy n the o ng uyê n t c : Hai
ố
đi m đ
c n i v i nhau n u v a thu c m t m t c a
ừ
ế
ể
đa di n này, v a thu c m t m t c a đa di n kia. C nh
ặ ủ
ộ
ệ
đó c h th y khi nó thu c c hai m t th y.
ặ
ộ
ỉ ấ
