
(IT4853) Tìm kiếm và trình diễn thông tin
Mô hình nhị phân độc lập

Giảng viên
TS. Nguyễn Bá Ngọc
Địa chỉ:
Viện CNTT & TT/BM HTTT/B1-603
Email:
ngocnb@soict.hust.edu.vn
Website: http://is.hust.edu.vn/~ngocnb
2

Nội dung chính
Tìm kiếm dựa trên xác suất
Mô hình nhị phân độc lập
Mô hình (Okapi) BM25
3
Xác suất trong tìm kiếm thông tin
Kết luận phù hợp là
không chắc chắn
Không bảo toàn
ngữ nghĩa
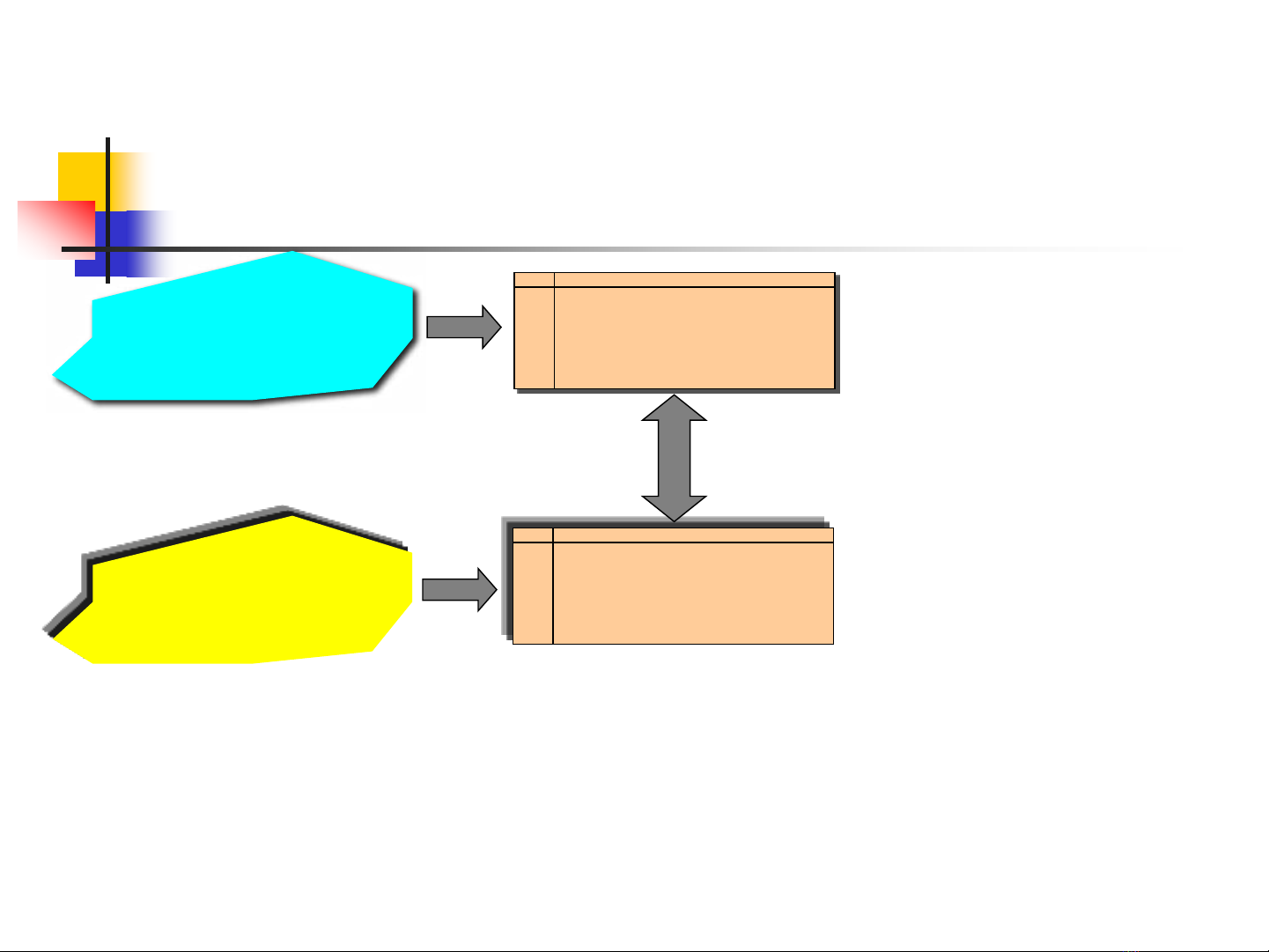
Nhu cầu thông tin
người dùng
Văn bản
Biểu diễn logic
truy vấn
Biểu diễn logic
văn bản
So sánh
So sánh văn bản và truy vấn dựa trên ký tự.
Kết quả so sánh thể hiện khả năng phù hợp về ngữ nghĩa.
Hoàn toàn có thể sử dụng xác suất để định lượng sự không
chắc chắn trong tìm kiếm.
4

Tìm kiếm dựa trên xác suất
Nguyên tắc xếp hạng xác suất
Mô hình nhị phân độc lập BIM
Okapi BM25
Mô hình ngôn ngữ.
5


























