BM Khoa học Máy tính • TOÁN RỜI RẠC • Fall 2005 • NGUYỄN ĐỨC NGHĨA
Các ứng dụng của
Bài toán luồng cực đại
Toán rời rạc – Fall 2005 NGUYỄN ĐỨC NGHĨA
Bộ môn KHMT
2
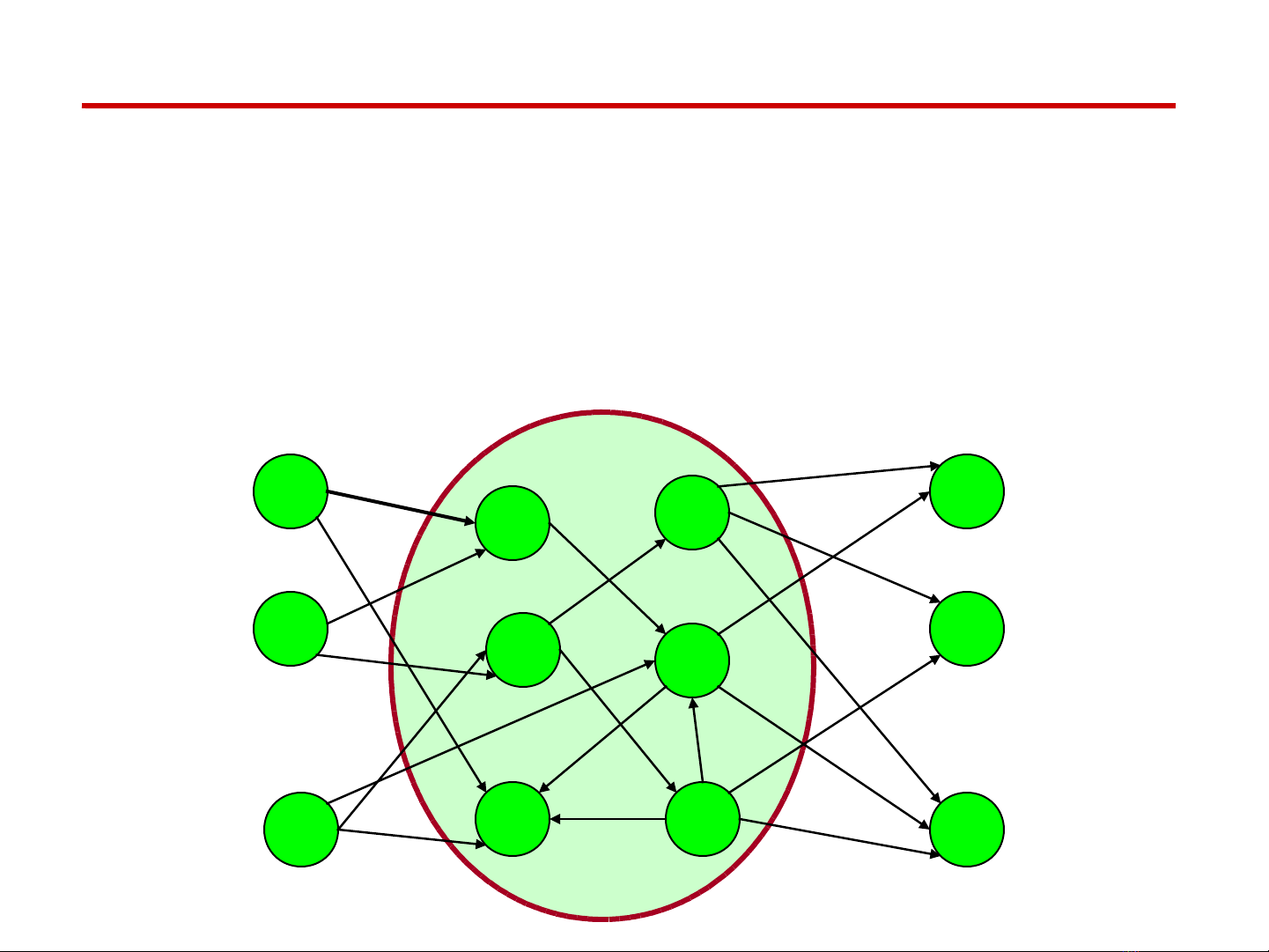
Max Flow Applications
s
t
Toán rời rạc – Fall 2005 NGUYỄN ĐỨC NGHĨA
Bộ môn KHMT
3
NỘI DUNG
Một số bài toán luồng tổng quát
–Bài toán với nhiều điểm phát và điểm thu
–Bài toán với hạn chế thông qua ở nút
Một số ứng dụng trong tổ hợp
–Bài toán cặp ghép cực đại trong đồ thị hai phía
–Độ tin cậy của mạng
Toán rời rạc – Fall 2005 NGUYỄN ĐỨC NGHĨA
Bộ môn KHMT
4
Một số bài toán luồng tổng quát
Toán rời rạc – Fall 2005 NGUYỄN ĐỨC NGHĨA
Bộ môn KHMT
5
M¹ng víi nhiÒu ®iÓm ph¸t vµ ®iÓm thu
XÐt m¹ng G víi p ®iÓm ph¸t s1, s 2,..., s p v i l ng ph¸t là ớ ượ a1,
a2, ..., ap vµ q ®iÓm thu t1, t2,..., tq v i l ng thu là bớ ượ 1, b2, ..., bq
Gi s ö r»ng luång c ã thÓ ®i tõ mét ®iÓm ph¸t bÊt kú ®Õn tÊt c
c¸c ®iÓm thu.
T×m luång cùc ®¹i tõ c¸c ®iÓm ph¸t ®Õn c¸c ®iÓm thu
s1
s2
sp
t1
t2
tq