
1
1
© TS. Lng Hu Tun
!
!!
! "
#
##
# $ %
2
© TS. Lng Hu Tun
#
##
#
$
$$
$ %
%%
%
&
&&
&
&
&&
&$
$$
$ '
''
'
"()'
"()'"()'
"()'
!&
!&!&
!&
$
$$
$ %
%%
% *
**
* +
++
+
#&
#&#&
#&,+
,+,+
,+
-
--
-
./
././
./
0&
0&0&
0&,.
,.,.
,. 1*
1*1*
1* +
++
+
+%
+%+%
+% '1
'1'1
'1
2&
2&2&
2&,.
,.,.
,. 1*
1*1*
1* +
++
+ 3
33
3 "4
"4"4
"4 +$
+$+$
+$
5&
5&5&
5&6
66
6 78
7878
78
9
99
9 78
7878
78
..
....
..
2
3
© TS. Lng Hu Tun
#
##
#
$
$$
$ %
%%
%
&
&&
&
&& $ %
&&: $
4
© TS. Lng Hu Tun
&&
&&&&
&&
$
$$
$ %
%%
%
: 1 +; + 9+%
1 2
,
D
t t S
t
rotH J H H J
∂
∂
= + − =
1 2
, 0
B
t t
t
rotE E E
∂
∂
= − − =
1 2
,n n
divD D D
ρ σ
= − =
1 2
0, 0
n n
divB B B
= − =
1 2
,n n
t t
divJ J J
ρ
σ
∂
∂
∂ ∂
= − − = −
D E
ε
=
B H
µ
=
J E
γ
=
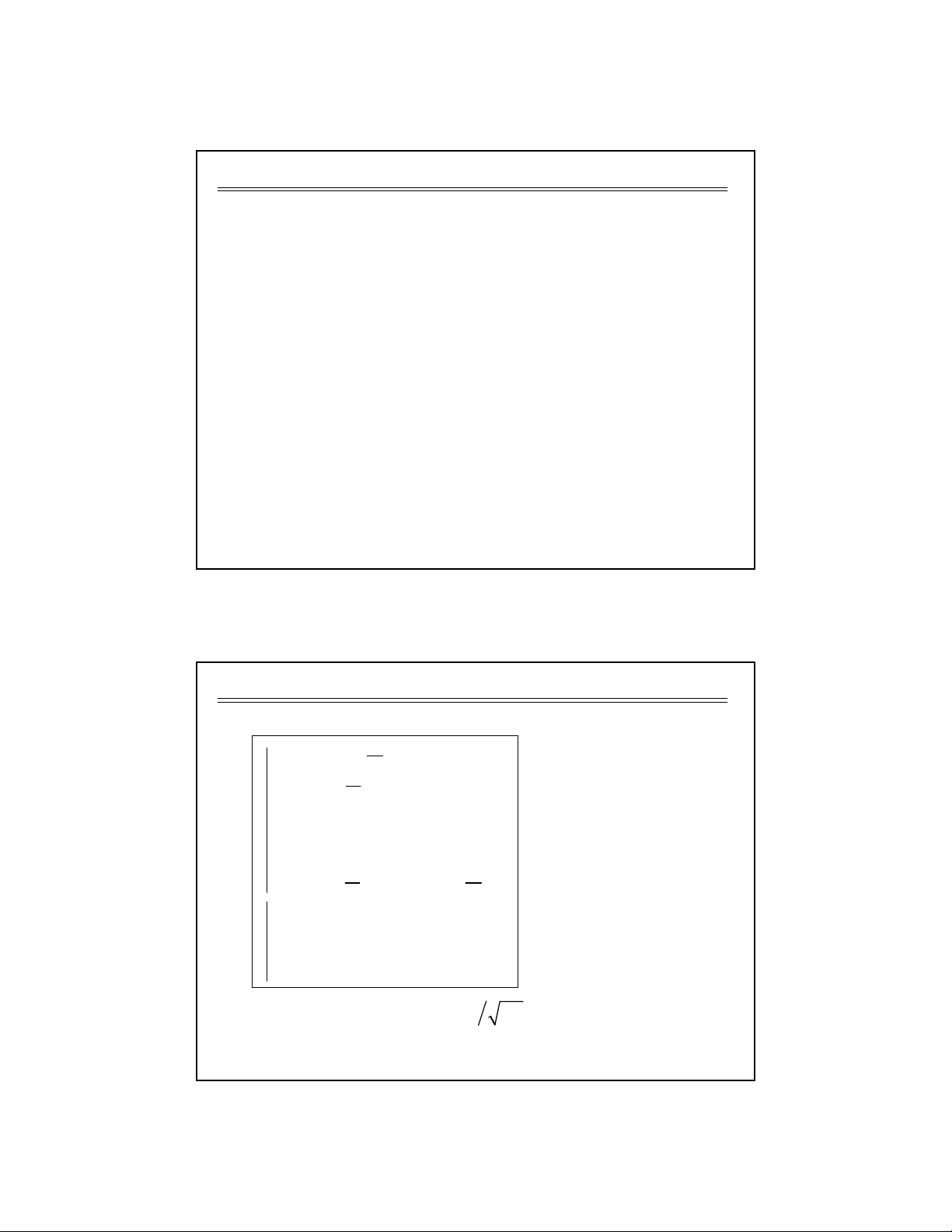
< $ .+ 1v
µε
=
"+ +% .$
P E H
= ×

3
5
© TS. Lng Hu Tun
&&
&&&&
&&:
::
:
$
$$
$
$ 3
0 ( )
divB IV
=
( ) 0 ( )
div rotA gtvt
=
B rotA
=
$ 3+% 3
( & )
B A
t t t
rotE rotA rot II hvtt
∂ ∂ ∂
∂ ∂ ∂
= − = − = −
( ) 0
A
t
rot E ∂
∂
+ =
A
t
E grad
ϕ
∂
∂
+ = −
+ '8
B rotA
=
A
t
E grad
ϕ
∂
∂
= − −
+ = * 9 8
( ) 0 ( )
rot grad gtvt
ϕ
=
6
© TS. Lng Hu Tun
#
##
#
$
$$
$ %
%%
%
&
&&
&
&
&&
&$
$$
$ '
''
'
"()'
"()'"()'
"()'
ε>+.µ>+.
&&6 "()'
"()' +$ 3
"()' +$ 3 ϕ
+ '8
&&$
&!&6 .+
A

4
7
© TS. Lng Hu Tun
6
66
6
"()'
"()'"()'
"()' 3
33
3 $
$$
$ 3
33
3
* 9 ?+@
( )
D
t
rotH J I
∂
∂
= +
( ) ( )
A
t t
rot rotA J grad
µ µε ϕ
∂ ∂
∂ ∂
= + − −
2
2
( ) ( ) ( , )
A
tt
grad divA A J grad gtvt hvtt
ϕ
µ µε µε
∂∂
∂∂
− ∆ = − −
0
t
divA
ϕ
µε
∂
∂
+ =
2
2
A
t
A J
µε µ
∂
∂
∆ − = −
6 "()' +$ 3
A
E
t
rotB J
µ µε
∂
∂
= +
A $B
2
2
( ) A
tt
A grad divA J
ϕ
µε µε µ
∂∂
∂∂
∆ − + − = −
8
© TS. Lng Hu Tun
6
66
6
"()'
"()'"()'
"()' 3
33
3 $
$$
$ 3+%
3+%3+%
3+%
( )
divD III
ρ
=
( , )
t
divA gtvt hvtt
ρ ε ϕ ε
∂
∂
= − ∆ −
0 ( )
t
divA Lorentz
ϕ
µε
∂
∂
+ =
2
2
t
ϕ
ϕ µε ρ ε
∂
∂
∆ − = −
6 "()' +$ 3 ϕ
( )
A
t
divE div grad
ρ ε ε ϕ
∂
∂
= = − −
A $B
2
2
2
t
ϕ
ρ ε ϕ µε
∂
∂
= − ∆ +
5
9
© TS. Lng Hu Tun
+
++
+ '8
'8'8
'8
2
2 2
1
v t
ϕ
ϕ ρ ε
∂
∂
∆ − = −
2
2 2
1A
v t
A J
µ
∂
∂
∆ − = −
1 :
v
µε
=3 +$ 1* .+
10
© TS. Lng Hu Tun
&&
&&&&
&&$
$$
$
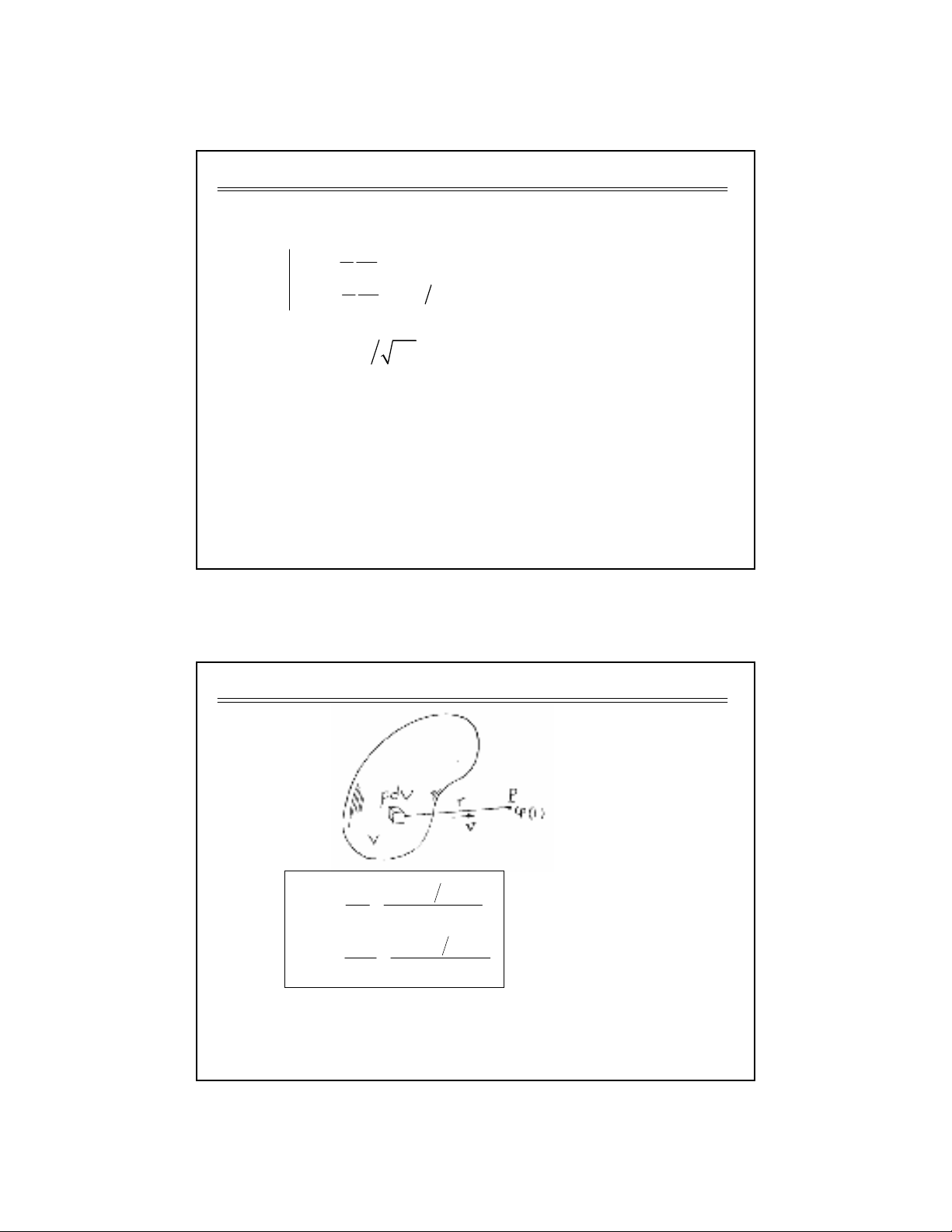
( )
( ) 4V
J t r v dV
A t r
µ
π
−
=
1 +; C+*D9+% 1 '
$ ; 9+ .
1 ( )
( ) 4V
t r v dV
tr
ρ
ϕπε
−
=











![Thí nghiệm Vật lí (BKEM-012): Tài liệu [Mô tả/Hướng dẫn/Bài tập,...]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251219/thanhlong020907@gmail.com/135x160/54561766129946.jpg)














