zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Khoa Học Tự Nhiên

Bài tập Nguyên lý thống kê kinh tế (Nhóm: B04)

Chia sẻ: Mưa Sao Băng | Ngày: | Loại File: DOC | Số trang:35

Báo xấu

530
lượt xem 58
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Mời các bạn cùng tham khảo nội dung bài tập "Nguyên lý thống kê kinh tế" dưới đây để nắm bắt được những nội dung về phân tích phương sai ANOVA, kiểm định phi tham số. Đây là tài liệu tham khảo hữu ích cho các bạn chuyên ngành Toán học.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài tập Nguyên lý thống kê kinh tế (Nhóm: B04)

Bài tập thống kê Họ và tên: BÀI TẬP NGUYÊN LÝ THỐNG KÊ MSSV: KINH TẾ Lớp: KT1390A2 Giáo viên: Huỳnh Thị Kim Uyên Nhóm: B04 Phần I/ Phân tích phương sai (ANOVA) I/ Phân tích phương sai một chiều. Phân tích phương sai một chiều là phân tích dựa trên ảnh hưởng của một nhân tố. Anova một chiều là kiểm định về sự bằng nhau của nhiều trung bình tổng thể có phân phối chuẩn, phương sai bằng nhau. Bài tập 1: Người ta tiến hành đo hàm lượng Alkaloid trung bình trong mướp đắng (Alkaloid trong mướp đắng có công hiệu lợi niệu hoạt huyết, tiêu viêm thoái nhiệt) ở 3 vùng khác nhau có số liệu như sau: Vùng 1: 7,5 6,8 7,1 7,5 6,8 6,6 7,8 Vùng 2: 5,8 5,6 6,1 6,0 5,7 Vùng 3: 6,1 6,3 6,5 6,4 6,5 6,3 Hỏi hàm lượng Alkaloid ở những vùng khác nhau có khác nhau hay không? Với =5%. Giải: Bài tập này yêu cầu kiểm định về sự bằng và khác nhau giữa các trung bình tổng thể dựa trên ảnh hưởng của hàm lượng Alkaloid nên giải theo phân tích phương sai một chiều. Cách 1: Cách thông thường (Tính tay) Giả thuyết: H 0 : Hàm lượng Alkaloid ở 3 vùng như nhau. H 1 : Hàm lượng Alkaloid ở 3 vùng khác nhau. Vùng 1 Vùng 2 Vùng 3 7,5 5,8 6,1 6,8 5,6 6,3 7,1 6,1 6,5 7,5 6,0 6,4 6,8 5,7 6,5 6,6 6,3 1
Bài tập thống kê 7,8 Nj 7 5 6 N=18 Tj 50,1 29,2 38,1 T=117,4 x ij2 359,79 170,7 242,05 xij2 = 772,54 i (Với i là biến chạy của dòng, j là biến chạy của cột) (117,4) 2 SST= 772,54 = 6,8311 18 (50,1) 2 (29,2) 2 (38,1) 2 (117,4) 2 SSA= + + = 5,326968 7 5 6 18 SSE= SST – SSA = 1,50414 Bảng ANOVA: Nguồn SS Df MS F Fk 1, n k , Yếu tố 5,326968 2 2,6635 26,5615 3,68 Sai số 1,50414 15 0,1003 Tổng cộng 6,8311 17 Quyết định: Ta có F = 26,5615 > F k 1, n k , nên bác bỏ H 0 chấp nhận H 1 . Kết luận: Với =5% hàm lượng Alkaloid có sai khác theo vùng. 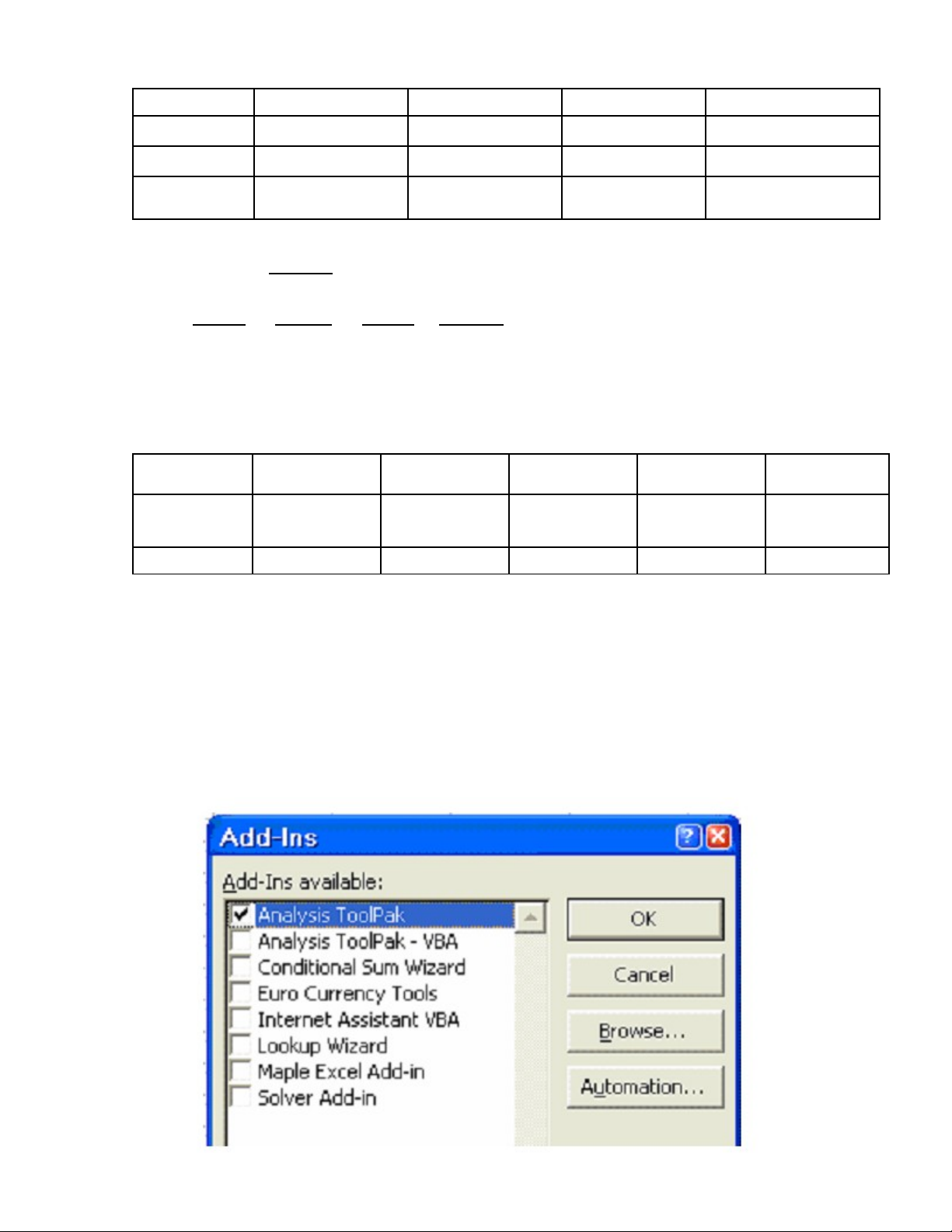Cách 2: Dùng Excel: (Vì em dùng Excel 2003 nên sử dụng Excel 2003) Nếu trong menu Tools chưa có mục Data Analysis… thì tiến hành cài Analysis ToolPak như sau: Tools \ AddIns \ chọn Analysis ToolPak\ OK. 2
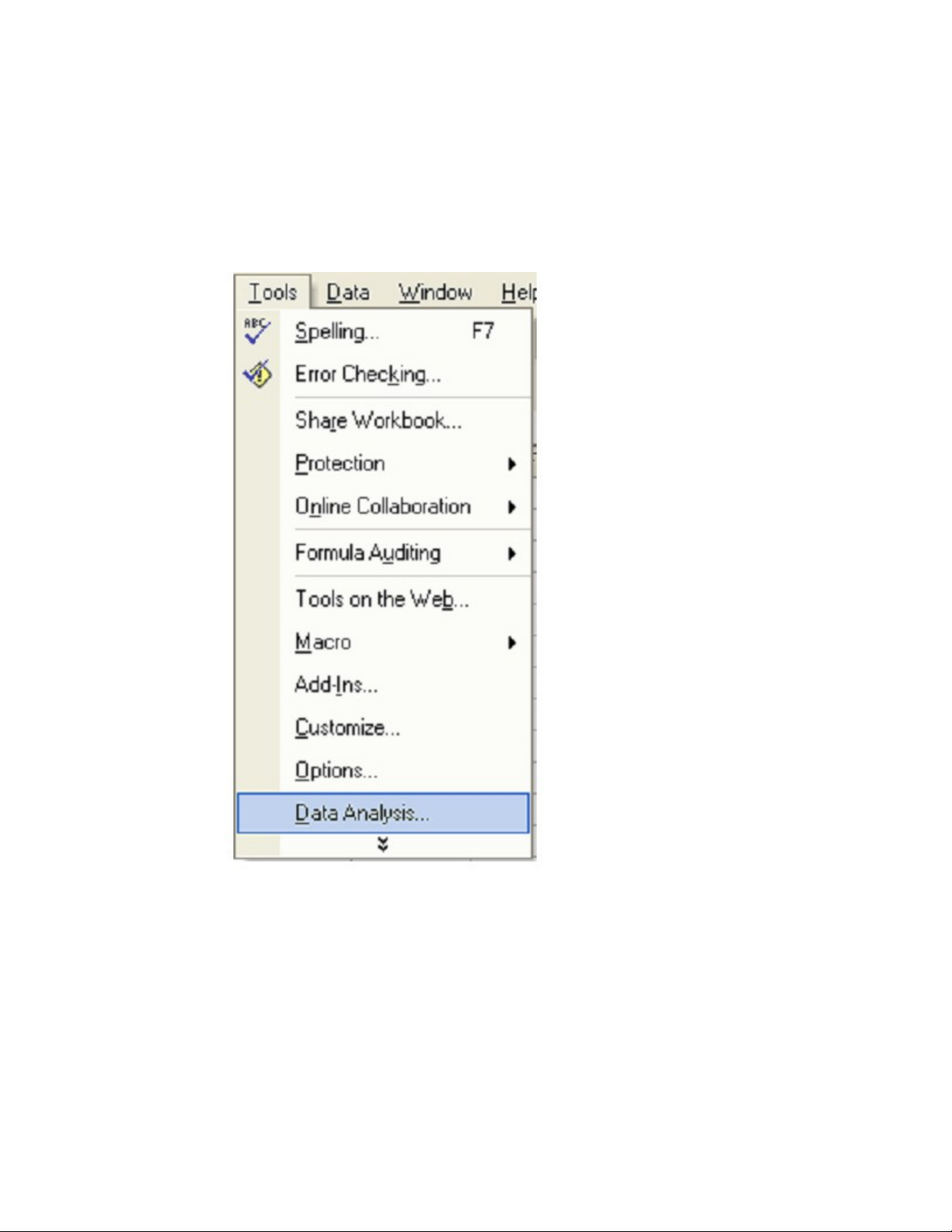
Bài tập thống kê Chọn Tools\ Data Analysis.. Nhập dữ liệu: 3
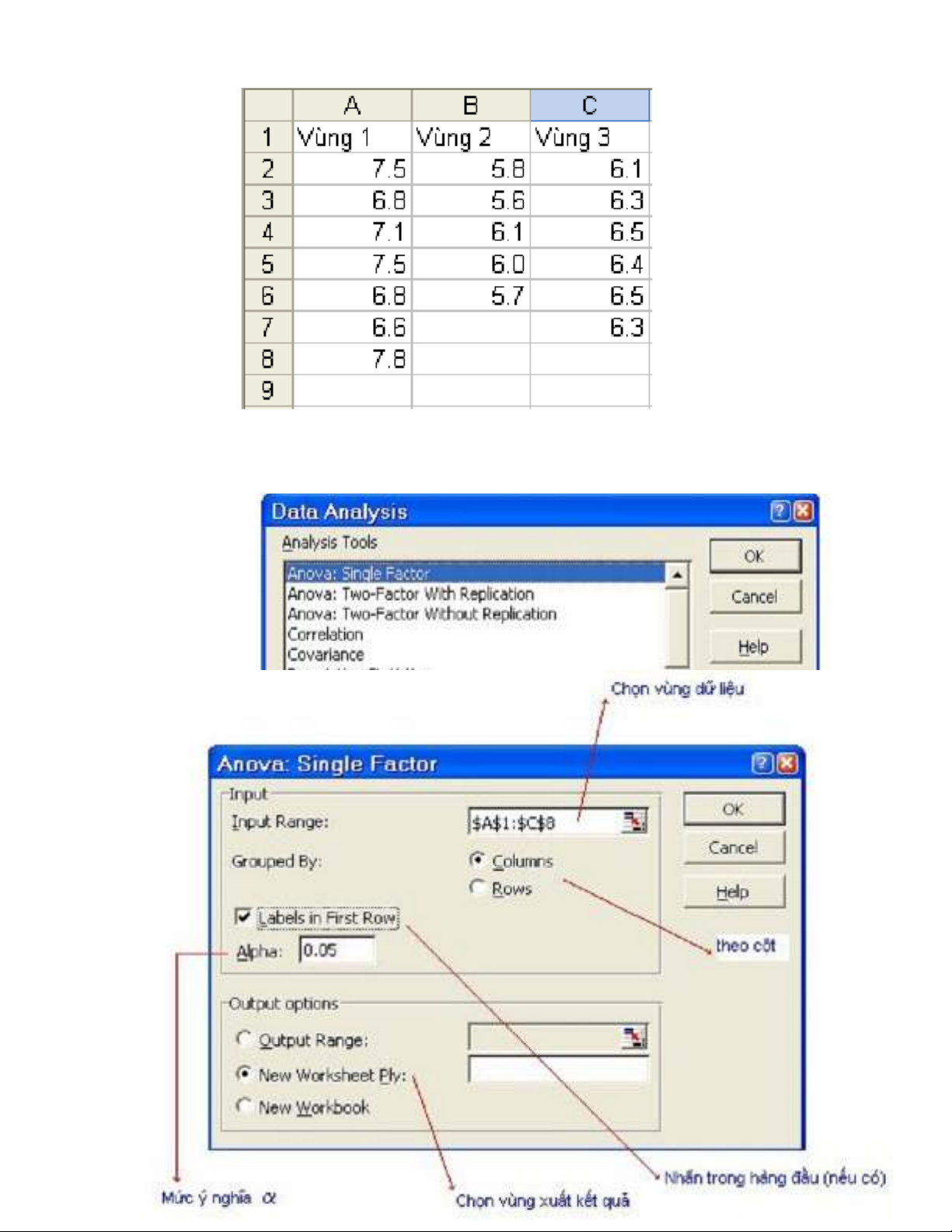
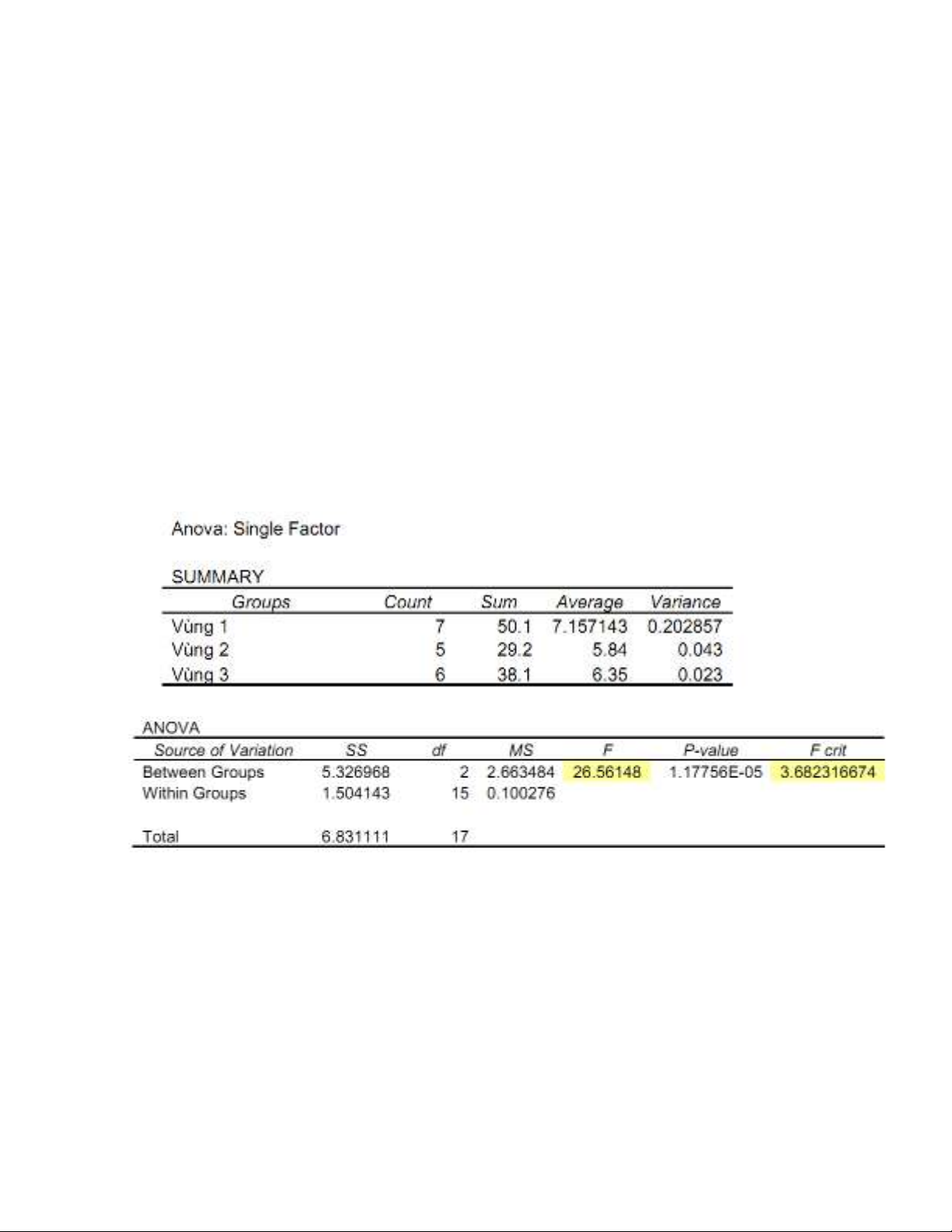
Bài tập thống kê Chọn: Anova: Single Facter: Chọn các mục như hình: 4
Bài tập thống kê Khi đó sẽ hiện ra bảng kết quả là: Quyết định: Cách 1: Ta so sánh cột F và F crit. Vì F = 26,56148> F crit = 3,682316674 => Bác bỏ H 0 chấp nhận H 1 . Cách 2: Đánh giá dựa vào Pvalue. Ta có: p = 1,17756E05 quá nhỏ => Bác bỏ H 0 chấp nhận H 1 . Kết luận: Với =5% hàm lượng Alkaloid có sai khác theo vùng. Bài tập 2: So sánh kết quả tăng trọng trung bình (kg) của trẻ 3 nhóm tuổi khác nhau sau khi sử dụng sản phẩm dinh dưỡng như nhau trong thời gian 1 năm 5
Bài tập thống kê Nhóm 1: Trẻ từ 1 tháng tuổi đến 12 tháng tuổi. 1,0 1,2 1,4 1,1 0,8 0,6 Nhóm 2: Trẻ từ 12 tháng tuổi đến 24 tháng tuổi. 2,0 1,8 1,9 1,2 1,4 1,0 1,5 1,8 Nhóm 3: Trẻ từ 24 tháng tuổi đến 36 tháng tuổi. 0,4 0,6 0,7 0,2 0,3 0,1 0,2 Hãy so sánh kết quả tăng trọng của 3 nhóm tuổi trên có như nhau không với =1%. Giải: Bài tập này yêu cầu kiểm định về sự bằng và khác nhau giữa các trung bình tổng thể dựa trên sự tăng trọng của từng nhóm tuổi khi sử dụng cùng một sản phẩm dinh dưỡng nên giải theo phân tích phương sai một chiều. Giả thuyết: H 0 : Kết quả tăng trọng của 3 nhóm tuổi là như nhau. H 1 : Kết quả tăng trọng của 3 nhóm tuổi là khác nhau. Nhóm 1 Nhóm 2 Nhóm 3 1,0 2,0 0,4 1,2 1,8 0,6 1,4 1,9 0,7 1,1 1,2 0,2 0,8 1,4 0,3 0,6 1,0 0,1 1,5 0,2 1,8 Nj 5 8 7 N=21 Tj 6,1 12,6 2,5 T=21,2 x ij2 6,61 20,74 1,19 xij2 =28,54 i (Với i là biến chạy của dòng, j là biến chạy của cột) (21,2) 2 SST = 28,54 = 7,1381 21 (6,1) 2 (12,6) 2 (2,5) 2 (21,2) 2 SSA = + + = 6,77795 5 8 7 21 SSE = SST – SSA = 0,36014 Bảng ANOVA: 6
Bài tập thống kê Nguồn SS Df MS F Fk 1, n k , Yếu tố 6,77795 2 3,38898 169,3816 6,01 Sai số 0,36014 18 0,0200079 Tổng 7,1381 20 cộng Quyết định: Ta có F = 169,3816 > F k 1, n k , = 6,01 nên bác bỏ H 0 chấp nhận H 1 . Kết luận: Với =1% kết quả tăng trọng của 3 nhóm tuổi là khác nhau. II/ Phân tích phương sai hai nhân tố không lặp (phân tích phương sai hai chiều có một quan sát trong cùng một ô) Phân tích phương sai hai nhân tố không lặp nhằm đánh giá sợ ảnh hưởng của 2 nhân tố trên các giá trị quan sát, đây là trường hợp mở rộng của phân tích phương sai một yếu tố. Bài tập 1: Chiết suất từ hoa hồng bằng 3 phương pháp khác nhau và 5 loại dung môi, ta có những kết quả sau: Phương pháp chiết suất B1 B2 B3 Dung môi A1 120 60 60 A2 120 70 50 A3 130 60 50 A4 150 70 60 A5 110 75 54 Hãy xét ảnh hưởng của phương pháp chiết xuất và dung môi đến kết quả chiết suất hoa hồng với =1%. Giải: Đề bài yêu cầu phân tích sự ảnh hưởng của 2 yếu tố phương pháp và dung môi đến kết quả chiết suất. Ta áp dụng phân tích phương sai 2 nhân tố không lặp. Cách 1: Tính thông thường. Giả thiết: 7
Bài tập thống kê H 0 : Dung môi không ảnh hưởng đến kết quả chiết suất. Phương pháp không ảnh hưởng đến kết quả chiết suất. H 1 : Dung môi ảnh hưởng đến kết quả chiết suất. Phương pháp ảnh hưởng đến kết quả chiết suất. B B1 B2 B3 Ti xij2 A j A1 120 60 60 240 21600 A2 120 70 50 240 21800 A3 130 60 50 240 23000 A4 150 70 60 280 31000 A5 110 75 54 239 20641 Tj 630 335 274 T=1239 xij2 80300 22625 15116 xij2 =118041 i i, j (Với i là biến chạy của dòng, j là biến chạy của cột) Ti 2 = 308321 i T j2 =584201 j (1239) 2 SST = 118041 = 155699,6 5 x3 308321 (1239) 2 SSA = = 432,2667 3 5 x3 584201 (1239) 2 SSB = = 14498,8 5 5 x3 SSE = SST – SSA – SSB = 768,5333 Nguồn SS Df MS F Yếu tố A SSA=432,2667 4 MSA=108,0667 F A = 1,1249 Yếu tố B SSB=14498,8 2 MSB=7249,4 F B = 75,4622 Sai số SSE=768,5333 8 MSE=96,0667 Tổng SST= 155699,6 14 Quyết định + kết luận: F A = 1,1249 Chấp nhận H 0 8
Bài tập thống kê  Với =1%, dung môi không ảnh hưởng đến kết quả chiết suất. F B = 75,4622 > F 2;8;1% = 8,649 => Bác bỏ H 0  Với =1%. Phương pháp ảnh hưởng đến kết quả chiết suất. Cách 2: Excel Nhập dữ liệu Chọn Tools\Data Analysis…\Anova: TwoFactor without replication. Làm theo các bước như hình: Kết quả : Anova: TwoFactor Without Replication 9
Bài tập thống kê Kiểm định theo cột: Giả thiết: H 0 : Phương pháp không ảnh hưởng đến kết quả chiết suất. Quyết định: p=6,42093E04% quá nhỏ => Bác bỏ H 0 Kết luận: Phương pháp ảnh hưởng đến kết quả chiết suất. Kiểm định theo hàng: Giả thiết: H 0 : Dung môi không ảnh hưởng đến kết quả chiết suất. Quyết định: p=40,9% quá lớn => Chấp nhận H 0 hoàn toàn. Kết luận: Dung môi ảnh hưởng đến kết quả chiết suất. Bài tập 2: 4 chuyên gia tài chính được yêu cầu dự đoán về tốc độ tăng trưởng (%) trong năm tới của 5 công ty sản xuất bánh kẹo. Dự đoán được ghi nhận như sau: 10
Bài tập thống kê Có thể nói rằng dự đoán tốc độ tăng trưởng trung bình là như nhau cho cả 5 công ty sản xuất bánh kẹo được không? =1%. Giải: Giả thiết: H 0 : Các chuyên gia dự đoán tốc độ tăng trưởng là như nhau. Các công ty sản xuất bánh kẹo đều có tốc độ tăng trưởng là như nhau. H 1 : Các chuyên gia dự đoán tốc độ tăng trưởng khác nhau. Các công ty sản xuất bánh kẹo đều có tốc độ tăng trưởng khác nhau. Chuyên gia xij2 Công ty A B C D Ti j 1 8 12 8,5 13 41,5 449,25 2 14 10 9 11 44 498 3 11 9 12 10 42 446 4 9 13 10 13 45 519 5 12 10 10 10 42 444 Tj 54 54 49,5 57 T=214, 5 xij2 606 594 497,2 659 xij2 =2356,25 i 5 i, j (Với i là biến chạy của dòng, j là biến chạy của cột) (214,5) 2 SST = 2356,25 = 55,7375 20 9211,25 (214,5) 2 SSA = = 2,3 4 20 11531,25 (214,5) 2 SSB = = 5,7375 5 20 SSE = SST – SSA – SSB = 47,7 Nguồn SS Df MS F 11
Bài tập thống kê Yếu tố A SSA=2,3 4 MSA=0,575 F A = 0,1447 Yếu tố B SSB=5,7375 3 MSB=1,9125 F B = 0,4811 Sai số SSE=47,7 12 MSE=3,975 Tổng SST= 55,7375 19 Quyết định + Kết luận: F A = 0,1447 Chấp nhận H 0 => Với =1%. Các chuyên gia dự đoán tốc độ tăng trưởng là như nhau. F B = 0,4811 Chấp nhận H 0 => Với =1%. Các công ty sản xuất bánh kẹo có tốc độ tăng trưởng như nhau. III/ Phân tích phương sai 2 nhân tố có lặp (có hơn một tham số trong một ô) Trong phân tích phương sai 2 nhân tố có lặp, mỗi yếu tố cột và hàng có thể có nhiều quan sát. Vậy nên ngoài việc kiểm định trung bình theo cột, hàng bằng nhau thì chúng ta còn có thể xem xét sự tương tác giữa yếu tố hàng và cột có ảnh hưởng đến hiện tượng nghiên cứu hay không. Bài tập 1: Hàm lượng cafein (mg) trong cà phê thu hái trong 2 mùa (mùa khô và mùa mưa) mỗi mùa lấy mẫu 3 lần đầu – giữa – cuối mùa và từ 3 tỉnh ở Tây Nguyên (Kon Tum, Gia Lai, Lâm Đồng) thu được kết quả sau: Tỉnh Mùa Thời điểm Kon Tum Gia Lai Lâm Đồng Đầu mùa 2,4 2,1 3,2 Khô Giữa mùa 2,4 2,2 3,2 Cuối mùa 2,5 2,2 3,4 Đầu mùa 2,5 2,2 3,4 Mưa Giữa mùa 2,5 2,3 3,5 Cuối mùa 2,6 2,3 3,5 (Với i là biến chạy của dòng, j là biến chạy của cột) 12
Bài tập thống kê Hãy cho biết hàm lượng cafein có khác nhau theo từng mùa hay không? Nếu có thì yếu tố mùa và miền (tỉnh khác nhau) có sự tương tác với nhau hay không? Với =0,05. Giải: Với đề bài cho hàng và cột có hơn 1 quan sát, yêu cầu xem xét sự tương tác giữa các yếu tố (hàng và cột) có ảnh hưởng đến đối tượng nghiên cứu không, ta dùng phân tích phương sai 2 yếu tố có lặp. Cách 1: Giải thông thường Giả thiết: H 0 : Hàm lượng cafein trong cà phê của các tỉnh là như nhau. Hàm lượng cafein trong cà phê ở 2 mùa mưa và mùa khô là như nhau. Không có sự tương tác giữa tỉnh và mùa màng đến hàm lượng cafein trong cà phê. H1 : Hàm lượng cafein trong cà phê của các tỉnh khác nhau. Hàm lượng cafein trong cà phê ở 2 mùa mưa và mùa khô khác nhau. Có sự tương tác giữa tỉnh và mùa màng đến hàm lượng cafein trong cà phê. Tỉnh Kon Tum Gia Lai Lâm Đồng T i** Mùa 2,4 2,1 3,2 Khô 2,4 7,3 2,2 6,5 3,3 9,8 23,6 2,5 2,2 3,3 2,5 3,2 3,4 Mưa 2,5 7,6 3,2 6,8 3,5 10,4 24,8 2,6 3,4 3,5 T * j* 14,9 13,3 20,2 T=48,4 (Với i là biến chạy của dòng, j là biến chạy của cột) 2 x ijk = 134,64 i , j ,k Ti*2* = 23,6 2 + 24,8 2 = 1172 i T*2j* = 14,9 2 + 13,3 2 + 20,2 2 = 806,94 j 13
Bài tập thống kê Tij2* = 7,3 2 + 7,6 2 + 6,5 2 + 6,8 2 + 9,8 2 + 10,4 2 = 403,74 i, j T 2 = 2342,56 2342,56 SST = 134,64 = 4,4978 18 1172 2342,56 SSA = = 0,08 9 18 806,94 2342,56 SSB = = 4,3478 6 18 403,74 SSE= 134,64 0,06 3 SSAB = SST – SSA – SSB – SSE = 0,01 Bảng ANOVA Nguồn SS Df MS F Yếu tố A 0,08 1 0,08 F A =16 (mùa) Yếu tố B (tỉnh) 4,3478 2 2,1739 F B =434,78 Tương tác AB 0,01 2 0,005 F AB =1 Sai số 0,06 12 0,005 Tổng 4,4978 17 Quyết định + kết luận: Ta có: F A =16 > F 1;12;5% = 4,7472  Bác bỏ H 0  Với =5%. Hàm lượng cafein khác nhau theo mùa. F B =434,78 > F 2;12;5% =3,8853  Bác bỏ H 0  Với =5%. Hàm lượng cafein khác nhau theo từng tỉnh thành. F AB =1 Với =5%. Không có sự tương tác giữa mùa và miền (tỉnh thành) đến hàm lượng cafein trong cà phê. Cách 2: Excel * Nhập dữ liệu 14
Bài tập thống kê * Chọn Tools\Data Analysis…\Anova: Two Factor With Replication Chọn như hình: Sau khi chạy chương trình máy tính sẽ hiện bảng ANOVA. 15
Bài tập thống kê Kiểm định theo cột: + Giả thiết: H 0 : Hàm lượng cafein trong cà phê ở 2 mùa mưa và mùa khô là như nhau. H 1 : Hàm lượng cafein trong cà phê ở 2 mùa mưa và mùa khô khác nhau. + Quyết định: Với =5% > p = 6,36194E12 => Bác bỏ H 0 + Kết luận: Với =5%, hàm lượng cafein trong cà phê ở 2 mùa mưa và mùa khô khác nhau. Kiểm định theo hàng: + Giả thiết: H 0 : Hàm lượng cafein trong cà phê ở các tỉnh thành là như nhau. H 1 : Hàm lượng cafein trong cà phê ở các tỉnh thành khác nhau. + Quyết định: p = 0,001761696 quá nhỏ => Bác bỏ H 0 . 16
Bài tập thống kê + Kết luận: Với =5%, hàm lượng cafein trong cà phê ở các tỉnh thành khác nhau. Kiểm định về sự tương tác: + Giả thiết: H 0 : Không có sự tương tác giữa tỉnh và mùa màng đến hàm lượng cafein trong cà phê. H 1 : Có sự tương tác giữa tỉnh và mùa màng đến hàm lượng cafein trong cà phê. + Quyết định: F = 0,396569457 Chấp nhận H 0 . + Kết luận: Với =5%, không có sự tương tác giữa tỉnh và mùa màng đến hàm lượng cafein trong cà phê. Bài tập 2: Điều tra mức tăng trưởng chiều cao (cm) của cây lúa theo loại đất trồng và loại phân bón khác nhau trong 1 tháng có kết quả: Loại đất 1 2 3 4 Loại phân 5,5 4,5 3,5 6,0 A 5,5 4,5 4,0 5,0 6,0 4,0 3,0 4,0 5,6 5,0 4,0 5,5 B 7,0 5,5 5,0 4,5 7,0 5,0 4,5 6,0 Hỏi sự khác nhau của mức tăng trưởng về chiều cao của cây lúa theo từng loại đất và phân bón. Với =5%. Giải: Giả thiết: H 0 : Mức tăng trưởng theo chiều cao của cây lúa theo loại đất trồng là như nhau. Mức tăng trưởng theo chiều cao của cây lúa theo loại phân bón là như nhau. Không có sự tương tác giữa phân bón và loại đất đến sự tăng trưởng theo chiều cao của cây lúa. 17
Bài tập thống kê H1 : Mức tăng trưởng theo chiều cao của cây lúa theo loại đất trồng khác nhau. Mức tăng trưởng theo chiều cao của cây lúa theo loại phân bón là khác nhau. Có sự tương tác giữa phân bón và loại đất đến sự tăng trưởng theo chiều cao của cây lúa. Đất 1 2 3 4 T i** Phân 5,5 4,5 3,5 6,0 A 5,5 17 4,5 13 4,0 10,5 5,0 15 55,5 6,0 4,0 3,0 4,0 5,6 5,0 4,0 5,5 B 7,0 19,6 5,5 15,5 5,0 13,5 4,5 16 64,6 7,0 5,0 4,5 6,0 T * j* 36,6 28,5 24 31 T=120,1 (Với i là biến chạy của dòng, j là biến chạy của cột) 2 x ijk = 624,61 i , j ,k Ti*2* = 7253,41 i T*2j* = 3688,81 j Tij2* = 1855,91 i, j T 2 = 14424,01 14424,01 SST = 624,61 = 23,60958 24 7253,41 14424,01 SSA = = 3,45042 12 24 3688,81 14424,01 SSB = = 13,80125 6 24 1855,91 SSE= 624,61 = 5,9733 3 SSAB = SST – SSA – SSB – SSE = 0,38458 Bảng ANOVA 18
Bài tập thống kê Nguồn SS Df MS F Yếu tố A 3,45042 1 3,45042 F A =9,2423 (mùa) Yếu tố B (tỉnh) 13,80125 3 4,60042 F B =12,3227 Tương tác AB 0,38458 3 0,1282 F AB =0,3434 Sai số 5,9733 16 0,37333 Tổng 23,60958 23 Quyết định + Kết luận: F A =9,2423 F 3;16;5% = 8,69  Bác bỏ H 0  Với =5%, mức tăng trưởng theo chiều cao của cây lúa theo loại đất trồng khác nhau F AB =0,3434
Bài tập thống kê Với mức ý nghĩa 5%, hãy kiểm định lượng người mua giày dép trước và sau Tết có thực sự khác nhau không? Giải: Giả thiết: H 0 : x y = 0 H 1 : x y 0 Giá trị kiểm định: Cửa hàng 1 2 3 4 5 6 7 8 9 10 T Trước Tết 50 60 65 100 80 90 77 85 40 67 Sau Tết 45 55 68 90 80 85 80 75 48 60 Chênh lệch 5 5 3 10 0 5 3 10 8 7 Hạng + 4 4 8,5 4 1,5 8,5 6 36,5 Hạng 1,5 7 8,5 T = min(T ,T ) = min(36,5;8,5)= 8,5 n =9 Quyết định: T = 8,5 Bác bỏ giả thuyết H 0 . Kết luận: Với =5%, lượng người mua giày dép trước và sau tết thực sự khác nhau. 2/ Mẫu lớn (n>20) Bài tập: Công ty sản xuất dầu gội đầu Sunsilk thực hiện một chiến dịch quảng cáo lớn nhằm tăng lượng mua hàng trong cả nước. Để kiểm tra chiến dịch quảng cáo có hiệu quả hay không, nhà sản xuất đã cử người điều tra trước và sau chiến dịch quảng cáo, mẫu là 200 người ở mỗi địa bàn trong 50 địa bàn dân cư (xã, phường) của thành phố Cần Thơ, những người được chọn sẽ được yêu cầu kể tên 5 loại dầu gội đầu. Ở từng địa bàn, trước và sau khi thực hiện chiến dịch quảng cáo, số lần goohi đầu dầu gội Sunsilk được ghi nhận lại. Chênh lệch trước và sau quảng cáo của số lần gội cũng được tính toán, xếp hạng theo giá trị tuyệt đối của chúng (không có chênh lệch 0). Tổng cộng hạng của các chênh lệch dương có giá trị nhỏ hơn và bằng 625. Hãy xem xét xem sau chiến dịch quảng cáo dầu gội đầu Sunsilk có được khách hàng biết đến nhiều hơn trước hay không với mức ý nghĩa 5%? 20

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.