Lêi nãi ®Çu
T«p« lµ m«n häc c¬ së cña Gi¶i tÝch hiÖn ®¹i, tµi liÖu viÕt vÒ nã rÊt nhiÒu
song rÊt Ýt tµi liÖu cã c¸c bµi tËp kÌm theo lêi gi¶i chi tiÕt minh ho¹ cho m«n
häc hÊp dÉn nh−ng t−¬ng ®èi trõu t−îng nµy. Nh»m gióp cho mét sè b¹n häc
viªn Cao häc To¸n c¸c kho¸ sau (KÓ tõ khãa 10) häc tËp ®ì vÊt v¶ vµ c¶m thÊy
thó vÞ h¬n m«n T«p«. Dùa vµo ch−¬ng tr×nh häc T«p« ®¹i c−¬ng cña Cao häc
10 To¸n, t¸c gi¶ thèng kª vµ gi¶i c¸c bµi tËp T«p« ®· gÆp trong ch−¬ng tr×nh
häc. §a sè c¸c lêi gi¶i tr×nh bµy chi tiÕt, cã nh÷ng bµi tËp hay t¸c gi¶ tr×nh bµy
nhiÒuc¸chgii®Ób¹n®äcthamkho.
V× n¨ng lùc cßn h¹n chÕ vµ ®©y chØ lµ c¸c lêi gi¶i mang tÝnh chñ quan cña
t¸c gi¶, ®iÒu kiÖn vËt chÊt kh«ng cho phÐp, nªn chØ cã thÓ tr×nh bµy ®−îc c¸c
bµi to¸n s¸t víi Bµi gi¶ng cña PGS TS TrÇn V¨n ¢n cho Häc viªn cao häc To¸n
kho¸ 9-10 §H Vinh.
Ch¾c ch¾n sÏ kh«ng tr¸nh khái thiÕu sãt, song còng mong nhËn ®−îc sù ñng
hé, ý kiÕn ®ãng gãp cña b¹n ®äc quan t©m ®Õn T«p«.
Cuèn s¸ch gåm bèn phÇn chÝnh:
I. Kh«ng gian T«p«
II. Kh«ng gian Mªtric
III. Kh«ng gian Compact
IV. Kh«nggianLiªnth«ng
Nh©n ®©y còng xin ®−îc c¶m ¬n anh NguyÔn Hång C−êng HV CH10 To¸n
®· ®Ò nghÞ t¸c gi¶ hoµn thµnh tµi liÖu nµy.
Vinh, ngµy 30 th¸ng 04 n¨m 2003
Ng« Quèc Chung12
Tr−êng PTDL Hermann Gmeiner Vinh, NghÖ An
1Email: nqchungv@yahoo.com
2Mobile: 0906236777
1
2
Kh«ng gian t«p«
Bµi 1 : Cho kh«ng gian t«p« X, E lµ tËp con cña Xta lu«n cã:
a)E®ãng ⇔E⊂E
b)E=E∪E
c)intE lµ tËp më lín nhÊt chøa trong E
d)Elµ tËp ®ãng nhá nhÊt chøa E
e)Elµ tËp më ⇔Elµ l©n cËn cña ∀x∈E
Chøng minh
a)Gi¶ sö E ®ãng mµ E⊂ E⇒∃®iÓm x∈Emµ x∈ E⇒x∈X\E
l¹i do E®ãng ⇒X\Emë ⇒∃l©n cËn Ucña xsao cho x∈U⊂X\E⇒
U∩E=∅⇒U∩E\{x}=∅tr¸i víi gi¶ thiÕt x∈E⇒E⊂E
Gi¶ sö E⊂E⇒∀x∈X\Eth× x∈ E⇒∃l©n cËn Ucña xsao cho
U∩E\{x}=∅⇒U∩E=∅(v× x∈ E)⇒U⊂X\E⇒X\Emë ⇒E®ãng
b)Gi¶ sö x∈E∪E⇒x∈EhoÆc x∈E.
NÕu x∈Erâ rµng x∈E.
NÕu x∈E⇒∀l©n cËn Ucña xth× ta cã
U∩E\{x}=∅vµ E\{x}⊂E\{x}
⇒U∩E\{x}=∅
⇒x∈E⊂E
⇒E∪E⊂E
Gi¶ sö x/∈X\E∪E⇒x/∈E⇒tånt¹il©ncËnUcña xsao cho
U∩E\{x}=∅mµ x/∈E⇒U∩E=∅⇒X\{E∪E}lµ tËp më mµ
E⊂E∪E⇒E⊂E∪E
c)Ta sÏ chøng minh r»ng mäi tËp më n»m trong E®Òu n»m trong intE.
ThËt vËy:
Gi¶ sö Ulµ tËp më bÊt k× sao cho U⊂E⇒∀x∈Uth× x∈U⊂E⇒E
lµ l©n cËn cña x⇒xlµ ®iÓm trong cña E⇒x∈intE
⇒U⊂intE
3
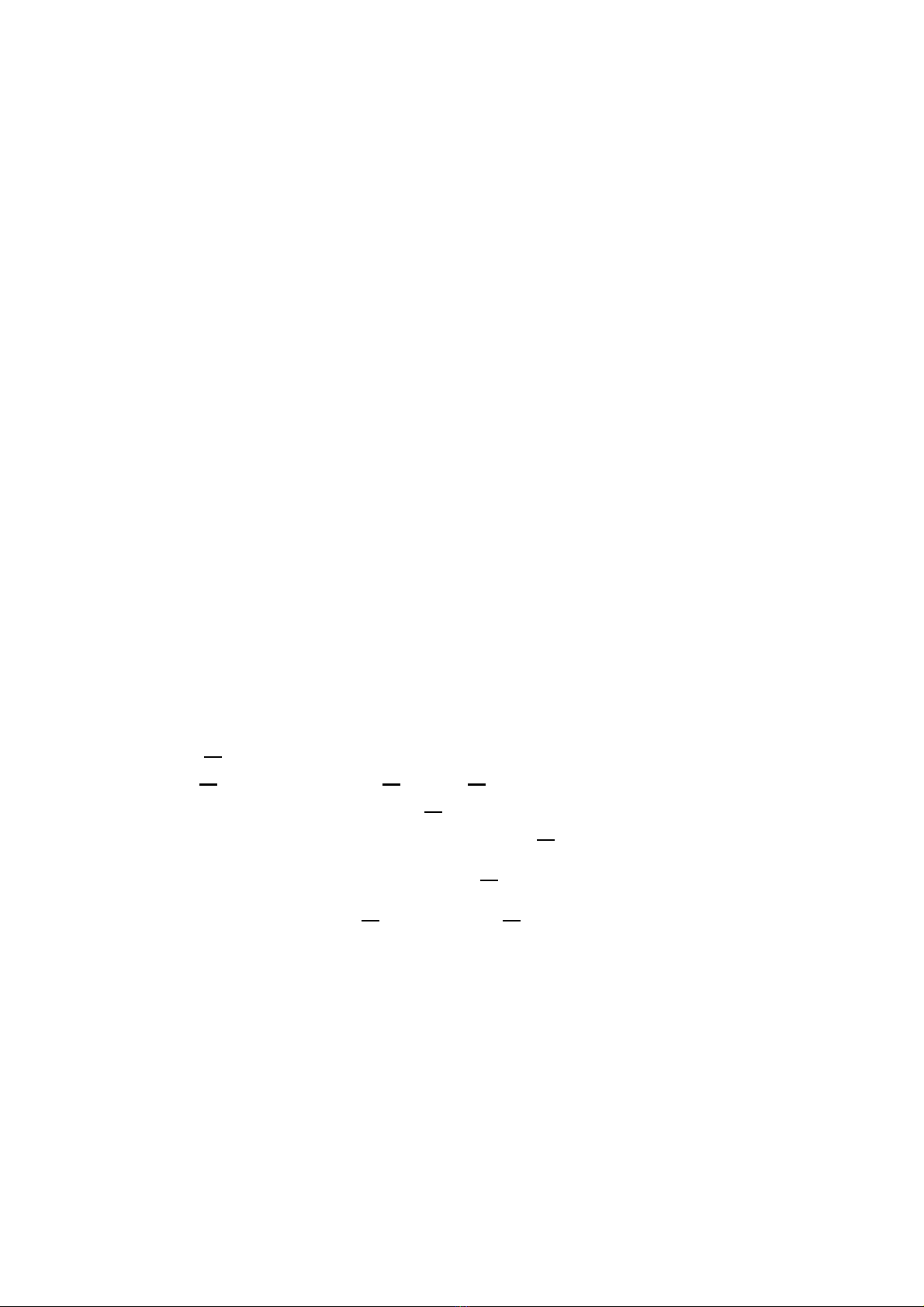
nqchungv@yahoo.com 4
B©ygiêtachøngminhintE lµ tËp më ®Ó hoµn thµnh chøng minh.
Víi mäi x∈intE ⇒Elµ l©n cËn cña x⇒∃Umë ®Ó
x∈U⊂E⇒U⊂intE ⇒intE lµ tËp më
d)Theo ®Þnh nghÜa
e)Râ rµngEmë ⇒Elµ l©n cËn cña ∀x∈E
Gi¶ sö Elµ l©n cËn cña mäi ®iÓm thuéc nã⇒∀x∈E,∃Uxlµ tËp më sao cho
x∈Ux⊂E⇒E=
x∈E
{x}⊂
x∈E
Ux⊂E⇒E=
x∈E
UxE
⇒Elµ tËp më
Bµi 2 : Mçi kh«ng gian tho¶ m·n tiªn ®Ò ®Õm ®−îc thø hai lµ kh¶ ly.
Chøng minh
C¸ch 1:
V× X lµ kh«ng gian tho¶ m·n tiªn ®Ò ®Õm ®−îcthø2,nªntrongXcãc¬së
Ω={Un}n∈N®Õm ®−îc
Víi mçi n∈Nta lÊy t−¬ng øng mét xn∈Un,vµ®ÆttËp
F={xn}n∈N
Râ rµng Flµ tËp ®Õm ®−îc, b©y giê ta sÏ chøng minh ¯
F=X. ThËt vËy:
Ta cã
(X\F)∩F=∅(1)
Gi¶ sö (X\F)=∅⇒∃x∈X\F,v×X\Fmë
⇒∃Un0∈Ωsao cho x∈Un0⊂X\F
Lóc ®ã tån t¹i xn0∈Fsao cho xn0∈Un0⊂X\F
⇒n0∈X\F∩F
§iÒu nµy tr¸i víi (1) vËy X\F=∅⇒X=F
C¸ch 2:
Gäi Ω={Un}n∈Nlµ c¬ së ®Õm ®−îccñaX.Ta®ÆttËp
F={xn}n∈N
trong®ãmçixn®−îc lÊy ra t−¬ng øng trong mét tËp Un.
Gi¶ sö Vlµ mét tËp më bÊt kú trong X⇒V=∪{Uα:Uα∈Ω}
⇒∃Uα0⊂V⇒∃xα0∈Fsao cho xα0∈Uα0⊂V
⇒F∩V=∅⇒ ¯
F=X
nqchungv@yahoo.com 5
Bµi 3 :
(a)Giaocñaméthät«p«tuúýtrªnXlµ mét t«p« trªn X
(b) Hîp cña hai t«p« trªn Xcã thÓ kh«ng lµ t«p« trªn X
(c) §èi víi mét hä tuú ý c¸c t«p« trªn X, tån t¹i mét t«p« duy nhÊt, mÞn
nhÊt trong c¸c t«p« th« h¬n mäi t«p« cña hä ®ã, vµ tån t¹i t«p« duy nhÊt, th«
nhÊt trong c¸c t«p« cña hä.
Chøng minh
(a)§iÒu nµy dÔ dµng chøng minh nhê vµo ®Þnh nghÜa, xin dµnh cho b¹n
®äc
(b)Ta sÏ chØ ra mét tËp Xcãhait«p«trªnnãmµhîpcñahait«p«nµy
kh«ng ph¶i lµ mét t«p« trªn X
Chän tËp X={a, b, c}. Víi hai t«p« lµ
Ω1={∅,{a, c},{a, b, c}}
Ω2={∅,{b, c},{a, b, c}}
DÔ dµng thö thÊy Ω1vµ Ω2lµ c¸c t«p« trªn X.
Lóc ®ã Ω=Ω1∪Ω2={∅,{a, c},{b, c},{a, b, c}} kh«ng ph¶i lµ mét t«p« trªn
X. ThËt vËy:
{a, c};{b, c}∈Ωnh−ng {a, c}∩{b, c}={c}∈ Ω
(c)Gäi U={Uα}α∈Ilµ mét hä c¸c t«p« trªn X
§Æt
T=<
α∈I
Uα
ta sÏ chøng minh Tlµ t«p« mÞn nhÊt trong c¸c t«p« th« h¬n mäi t«p« cña hä U.
ThËt vËy, gi¶ sö Ulµ mét t«p« bÊt k× th« h¬n c¸c t«p« cña hä U
⇒U⊂Uα,∀α⇒U⊂<
α∈I
Uα=T⇒TmÞn h¬n U⇒(®pcm )
Gäi hä t«p«
β={T:TmÞn h¬n mäi t«p« cña hä U}
§Æt
T=<
T∈β
T
Ta sÏ chøng minh Tlµ t«p« th« nhÊt trong c¸c t«p« mÞn h¬n mäi t«p« cña hä
U.ThËtvËy
Gi¶ sö Ulµ t«p« bÊt kú mÞn h¬n mäi t«p« cña hä U⇒U=Tβ0nµo ®ã