
A Numerical Analysis of The Wave Forces on
Vertical Cylinders by Boundary Element Method
Msc. Cao Tan Ngoc Than*
** Graduate School, Cheju National University, Cheju, Korea, 690756 -Speaker
April 18,2009
Contents
Giới thiệu
Phương Pháp Phần TửBiên
Kết quảphân tích và kiểm tra
Kết luận
I.Introduction
Gaàn ñaây coùraát nhieàu loïai coâng trình bieån khaùc nhau ñöôïc xaây döïng treân moät
nhoùm coïc nhö laøcoät troøn. Vì theásöïtöông taùc giöõa soùng vaømoät nhoùm coät troøn
caàn ñöôïc nghieân cöùu moät caùch chính xaùc ñeåñaùnh giaùsöïoån ñònh cuûa coâng trình
Coùraát nhieàu nhaønghieân cöùu vaøcoâng trình nghieân cöùu veàsöïtöông taùc giöõa soùng
vaømoät nhoùm coät nhö laø:
Chakrabarti (1978) vaøOhkusu (1974) – phaân tích veàlöïc cuûa soùng leân moät nhoùm
coät
Kim vaøPark (2007)- phaân tích veàlöïc cuûa soùng leân moät coät troøn rieâng leõbaèng
phöông phaùp phaàn töûbieân
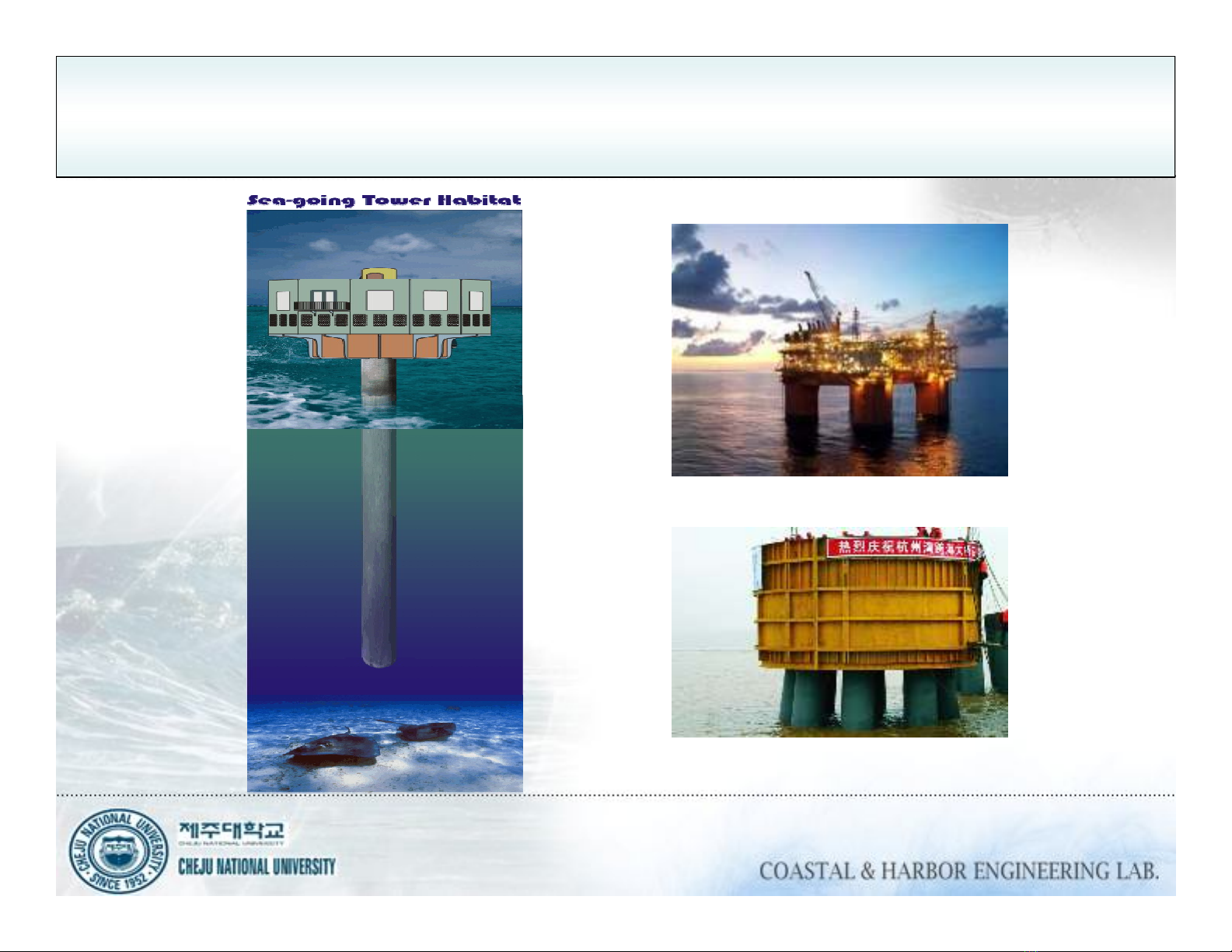
Research Object
Phöông phaùp tính löïc cuûa soùng taùc duïng leân moät nhoùm coät söûduïng phöông phaùp
phaàn töûbieân ñöôïc phaùt trieån ñeågiaûi quyeát hieän töôïng nhieãu xaïcuûa soùng bôûi moät
nhoùm coät.
Moâhình cuûa moät coät, hai coät vaøba coät ñöôïc söûsuïng trong nghieân cöùu naøy.
Ñeåkieåm chöùng keát quaû, keát quaûtính toaùn löïc cuûa soùng taùc duïng leân moät coät, hai coät,
ba coät trong nghieân cöùu naøy ñöôïc so saùnh vôùi keát quaûtính toaùn cuûa MaâcCamy and
Fuchs (1954), Chakrabaûti (1978) va cuûa Ohkusu (1974)
Soùng daâng leân (run-up) vaøsöïphaân boáchieàu cao cuûa soùng xung quanh coät (wave
height distribution) cuõng ñöôïc tính toaùn trong nghieân cöùu naøy.
















