Bé §Ò Tæng Hîp - M«n TrÝ TuÖ Nh©n T¹o – K2CN4
Đ 1ề
Câu 1.(3đ)
Trình bày s khác nhau gi a thu t toán và thu t gi i Heuristics. Hãy nêu 1 ví dự ữ ậ ậ ả ụ
v thu t gi i Heuristicsề ậ ả
Câu 2.(7đ)
a. Trình bày thu t gi i Robinson. ậ ả
b. Áp d ng thu t gi i Robinson, ch ng minh bài toán sau: ụ ậ ả ứ
¬p ∨ q , (s ∨ ¬ q) ∧ (r ∨ ¬s) , p ∧ u ⇒ r, u
c. Hãy xây d ng cây đ nh danh và tìm lu t theo ph ng pháp vector đ c tr ng c aự ị ậ ươ ặ ư ủ
Quinlan đ xác đ nh m t lo i qu đ c hay không đ c theo b ng s li u sau.ể ị ộ ạ ả ộ ộ ả ố ệ
Tên VịMàu VỏĐ cộ
A Ng tọĐỏNh nẵkhông
B Cay ĐỏNh nẵkhông
C Chua Vàng Có gai Không
D Cay Vàng có gai Đ cộ
E Ng tọTím Có gai Không
F Chua Vàng Nh nẵKhông
G Ng tọTím Nh nẵKhông
H Cay Tím có gai Đ cộ
Đ 2 (có gi i) trang 13)ề ả
Câu 1(3 đ)
Trình bày khái ni m hàm heuristics.ệ: Xây d ng hàm đánh giá h cho bài toán ự ở
b ng 1ả để gi i bài toán ảTACI sau:
3 2 6 1 2 3
1 5 4 8 4
7 8 7 6 5
TiTG
B ngả 1
Câu 2(7 đ)
a. Trình bày thu t gi i Aậ ả *.
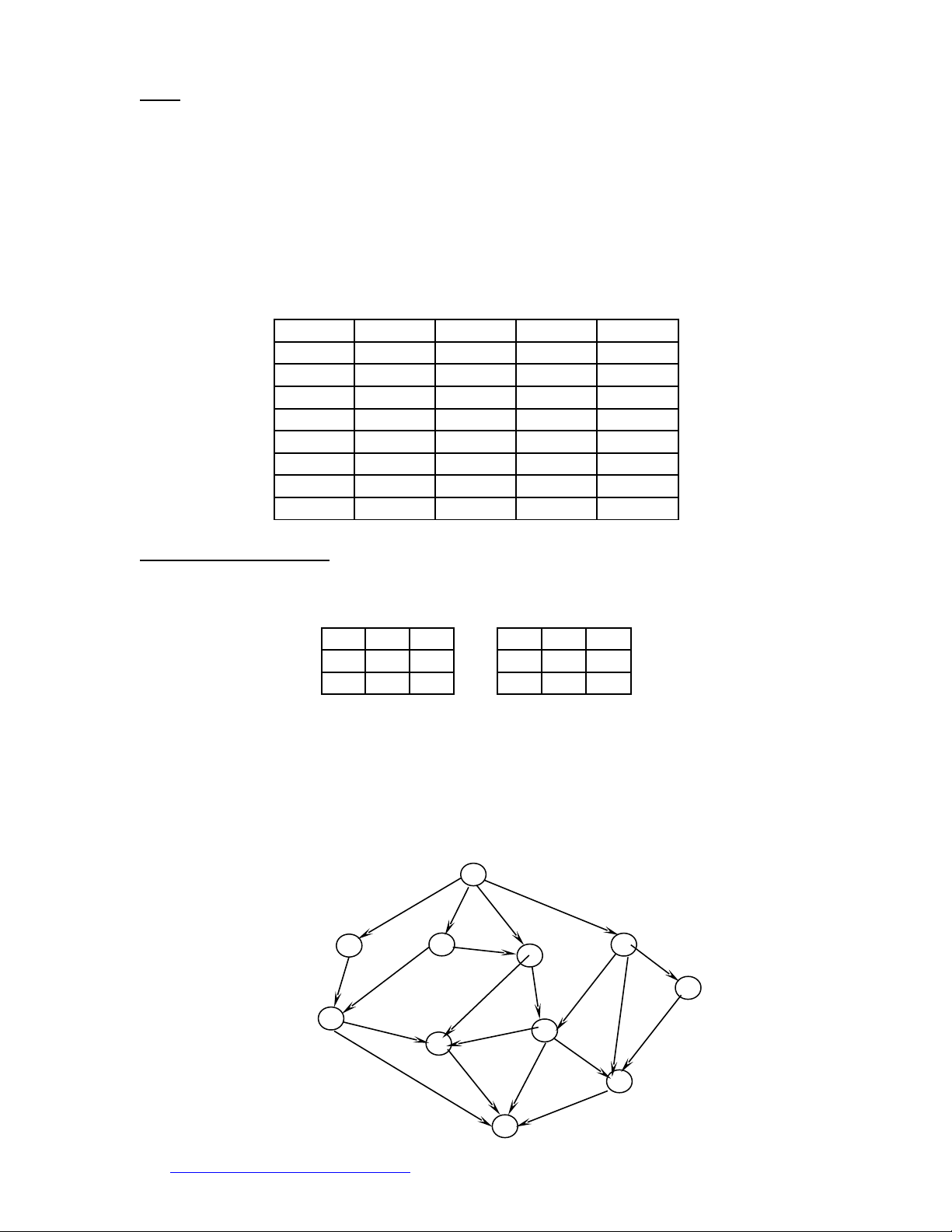
b. Gi i bài toán tìm đ ng đi ng n nh t t A đ n B trong đ th không gian tr ngả ườ ắ ấ ừ ế ồ ị ạ
thái ởHình 1 theo thu t gi i A*. (Giá tr c nh các đ nh là hàm đánh giá h(T), c nh cácậ ả ị ạ ỉ ạ
cung là đ dài cung).ộ
amittkduong@gmail.com - k2cn4.n-stars.org – 4rum K2CN4 1
0
E
K
C
H
D
I
E
K
G
H
B
A
I
F
G
N
22
16
2
4
25
30
2
0
12
14
13
17
9
20
11
9
17
10
16
5
7
6
18
12 15
10
813
12 12
8
10
Hình 1
Bé §Ò Tæng Hîp - M«n TrÝ TuÖ Nh©n T¹o – K2CN4
Đ 3ề
Câu 1 (3đ)
a. Trình bày thu t gi i V ng H o.ậ ả ươ ạ
b. Áp d ng thu t toán V ng h o, ch ng minh bài toán sau:ụ ậ ươ ạ ứ
p ∨ ¬q , (¬s ∨ ¬q) ∧ (r ∨s) , ¬p ∧ u ⇒ r ∨ u
Câu 2 : (7đ)
a. Trình bày thu t gi i A ậ ả KT .
b. Dùng thu t toán A ậKT đ gi i bài toán TACI sau:ể ả
Tr ng thái ban đ u ạ ầ Tr ng thái k t thúcạ ế
Đ 4ề
Câu 1: (4đ)
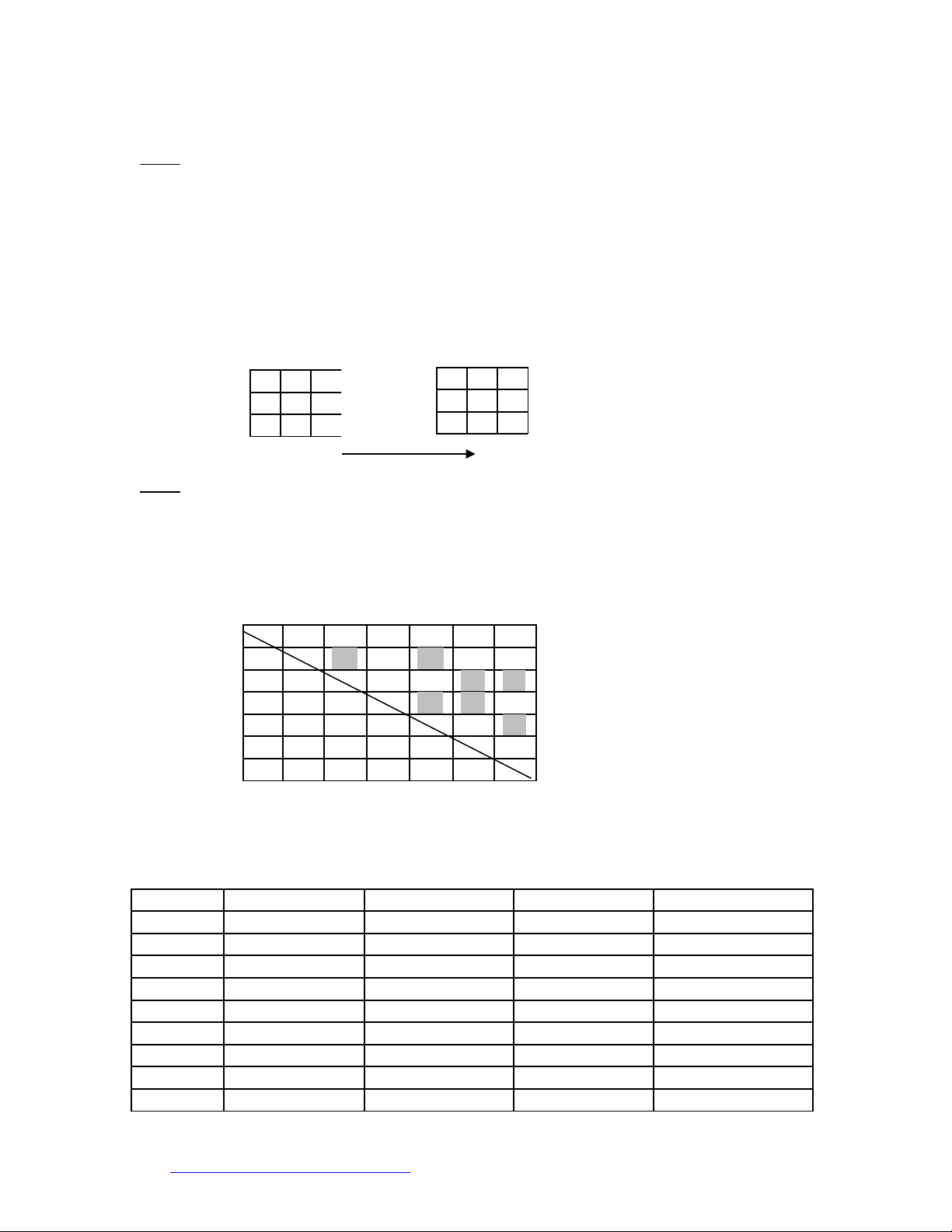
Có 6 đ i bóng thi đ u vòng tròn (l t đi). Bi t r ng :ộ ấ ượ ế ằ
-Đ i A đã đ u v i d i B và đ i D.ộ ấ ớ ộ ộ
-Đ i C đã đ u v i d i D và đ i Fộ ấ ớ ộ ộ
-Đ i D đã đ u v i d i A và đ i F.ộ ấ ớ ộ ộ
-Đ i B đã đ u v i d i E và đ i F.ộ ấ ớ ộ ộ
A B C D E F
A AB AC AD AE AF
B BC BD BE BF
C CD CE CF
D DE DF
E EF
F
M i đ i ch có đ c thi đ u 1 tr n trong 1 tu n.ỗ ộ ỉ ượ ấ ậ ầ
Ch có 2 đ i thamgia 1 tr n đ u.ỉ ộ ậ ấ
Hãy x p l ch thi đ u sao cho s tu n di n ra các tr n đ u còn l i là ít nh t ? (Dùngế ị ấ ố ầ ễ ậ ấ ạ ấ
thu t toán tô màu)ậ
Câu 2: (6đ) Cho b ng quan sát :ả
STT Quang c nhảNhi t đệ ộ Gió Picnic
1 N ngắCao NhẹKhông
2 M aưTh pấM nhạKhông
3 Râm mát TB NhẹĐ cượ
4 N ngắTB M nhạKhông
5 M aưCao M nhạKhông
6 Râm mát Th pấM nhạĐ cượ
7 M aưTB NhẹKhông
8 N ngắTB NhẹĐ cượ
9 M aưTh pấNhẹKhông
amittkduong@gmail.com - k2cn4.n-stars.org – 4rum K2CN4
L E Y
O U
Q D N
L E
Q U Y
D O N
2
Bé §Ò Tæng Hîp - M«n TrÝ TuÖ Nh©n T¹o – K2CN4
Xác đ nh đi u ki n nh th nào đ t ch c ị ề ệ ư ế ể ổ ứ Đ cượ hay Không bu i picnic ?(Dùngổ
thu t toán Quinlan)ậ
Đ 5:ề
BAØI 1:(3 ÑIEÅM)
Giaû söû coù 9 cuoäc minting a,b,c,d,e,f,g,h,i ñöôïc toå chöùc.
Moãi cuoäc mitting ñöôïc toå chöùc trong moät buoåi. Caùc cuoäc
mitting sau khoâng ñöôïc dieãn ra ñoàng thôøi:
ae,bc,cd,ed,abd,ahi,bhi,dfi,dhi,fgh. Haõy söû duïng thuaät toaùn
toâ maøu toái öu ñeå boá trí caùc cuoäc mitting vaøo caùc buoåi
sao cho soá buoåi dieãn ra laø ít nhaát.
BAØI 2: (3 ÑIEÅM)
Cho ñoà thò coù ma traän chi phí nhö sau
Haõy söû duïng
thuaät giaûi
GTS2 ñeå tìm
haønh trình toát
nhaát vôùi p = 4
(v1=1, v2=2, v3=4, v4=6.
BAØI 3:(4 ÑIEÅM)
Söû duïng thuaät toaùn QuinLan ñeå giaûi quyeát baøi
toaùn sau:
Ñeå xaùc ñònh ngöôøi chaâu AÙ hay ngöôøi chaâu AÂu khi
xem xeùt moät nhoùm ngöôøi caên cöù treân hình daùng,
chieàu cao vaø giôùi tính theo baûng sau:
amittkduong@gmail.com - k2cn4.n-stars.org – 4rum K2CN4
1 2 3 4 5 6
1
2
3
4
5
∞
2
04
23
06 25
1
2
∞
1
67 33 19
2
35
∞
2
814 9
1
29 2
4
∞
31 15
1
47 2
11
5
∞
45
6 3
61
51
65 20
5
∞
3
Bé §Ò Tæng Hîp - M«n TrÝ TuÖ Nh©n T¹o – K2CN4
Ñaëc ñieåm
Ngöôøi Daùng Chieàu cao Giôùi tính Thuoäc chaâu
1 To Trung bình Nam Chaâu AÙ
2 Nhoû Thaáp Nam Chaâu AÙ
3 Nhoû Trung bình Nam Chaâu AÙ
4 To Cao Nam Chaâu AÂu
5 Nhoû Trung bình Nöõ Chaâu AÂu
6 Nhoû Cao Nam Chaâu AÂu
7 Nhoû Cao Nöõ Chaâu AÂu
8 To Trung bình Nöõ Chaâu AÂu
amittkduong@gmail.com - k2cn4.n-stars.org – 4rum K2CN4 4
Bé §Ò Tæng Hîp - M«n TrÝ TuÖ Nh©n T¹o – K2CN4
Đ 6ề
BAØI 1.:(3 ÑIEÅM)
Söû duïng Thuaät giaûi AKT – Tìm kieám vôùi tri thöùc boå sung (Algorthm for
Knowled geable Tree Search) ñeå giaûi baøi toaùn Taci theo caùc traïng
thaùi: 2 8 3
1 6 4
7 5
Traïng thaùi ñaàu Traïng thaùi ñích
BAØI 2.:(3 ÑIEÅM)
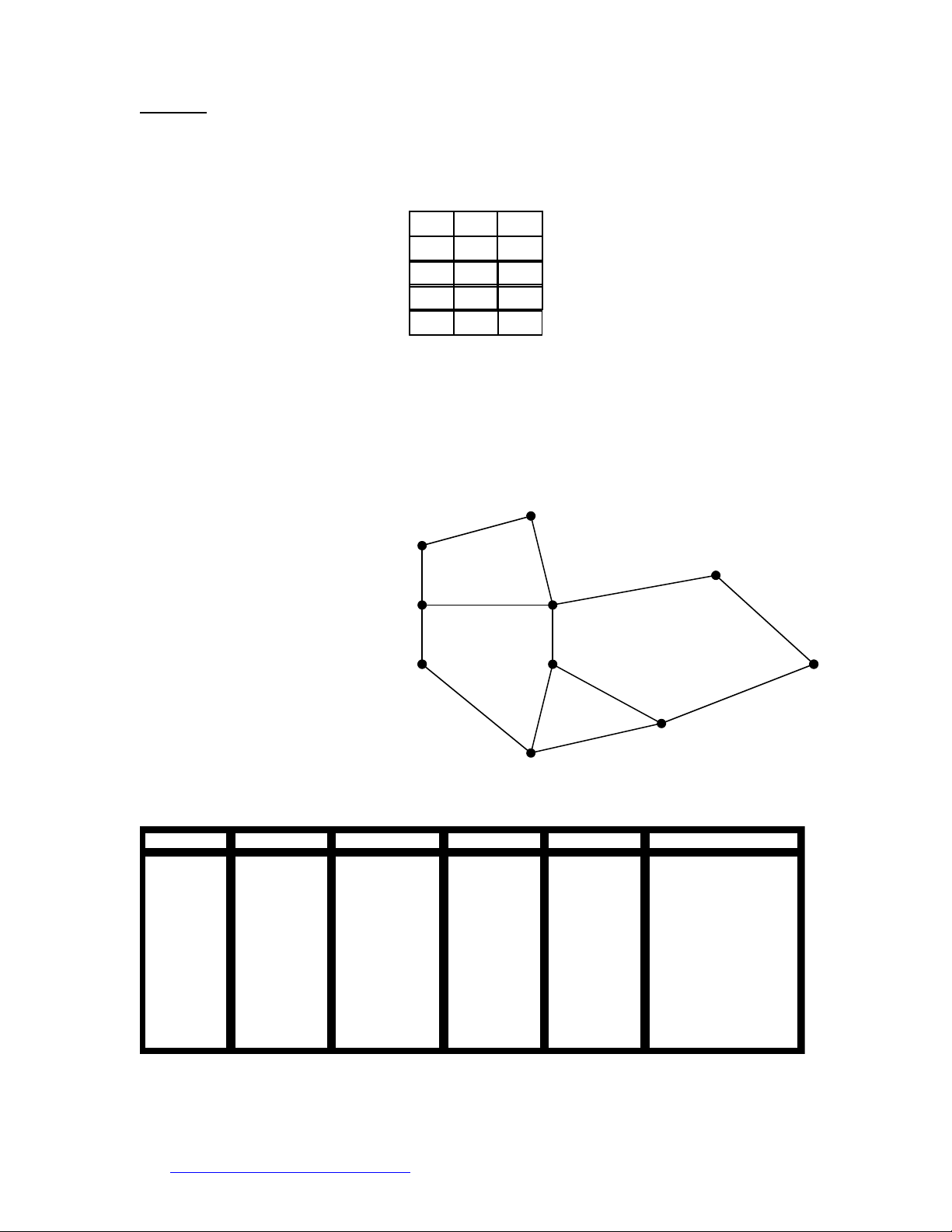
Haõy söû duïng thuaät giaûi A* ñeå tìm ñöôøng ñi ngaén nhaát
töø thaønh phoá A ñeán thaønh phoá B bieát khoaûng caùch
öôùc löôïng töø caùc thaønh phoá ñeán thaønh phoá B ñöôïc cho
nhö sau:
Ñænh khoaûng caùch öôùc löôïng
Z 374
A 366
T 329
C 160
R 193
P 98
B 0
F 178
S 253
O 380
BAØI 3.:(4 ÑIEÅM)
Söû duïng phöông phaùp ñoä ño hoãn loaïn ñeå giaûi baøi toaùn
sau:
Theo baûng döõ lieäu xaùc ñònh hieäu quaû cuûa vieäc söû
duïng kem chaùy naéng
Teân Maøu toùc Chieàu cao Caân naëng Duøng kem Keát quaû
1. Sarah Vaøng Trung bình Nheï Khoâng Chaùy naéng
2. Dana Vaøng Cao Trung bình Coù Khoâng chaùy naéng
3. Alex Naâu Luøn Trung bình Coù Khoâng chaùy naéng
4. Annie Vaøng Luøn Trung bình Khoâng Chaùy naéng
5. Emily Ñoû Trung bình Naëng Khoâng Chaùy naéng
6. Pete Naâu Cao Naëng Khoâng Khoâng chaùy naéng
7. John Naâu Trung bình Naëng Khoâng Khoâng chaùy naéng
8. Katie Vaøng Luøn Nheï Coù Khoâng chaùy naéng
amittkduong@gmail.com - k2cn4.n-stars.org – 4rum K2CN4
1 2 4
8 5
7 6 3
5
O
Z
A
T
CP
B
F
R
S
75
118
70
151
99 120
100
146
80
140
110
60
97