Chương 6.: HÀM SỐ HAI BIẾN SỐ

Chia sẻ: Tran Manh Hung | Ngày: | Loại File: DOC | Số trang:14

Thêm vào BST

Báo xấu

205
lượt xem 49
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

6.1.1. Miền biến thiên của hai biến số. Ký hiệu: R là tập hợp các số thực...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Chương 6.: HÀM SỐ HAI BIẾN SỐ

Ch¬ng 6. Hµm sè hai biÕn sè 6.1. §Þnh nghÜa hµm hai biÕn sè 6.1.1. MiÒn biÕn thiªn cña hai biÕn sè. Ký hiÖu: R lµ tËp hîp c¸c sè thùc ⇒ R = (−∞;+∞ ). R2 = {(x,y): x, y ∈ R}. §Þnh nghÜa 6.1. (i) Cho M0 =(x0,y0) ∈ R2, M =(x,y) ∈ R2. Th× kho¶ng c¸ch tõ M0 ®Õn M ®îc ký hiÖu vµ x¸c ®Þnh nh sau: ( x − x 0 ) 2 + ( y − y0 ) 2 . d(M0; M) = (6.1) (ii) Ta nãi ®iÓm M tiÕn dÇn tíi ®iÓm M0 trong R2 (ký hiÖu: M→M0) nÕu lim d ( M , M 0 ) = 0 . (6.2) M →M0  x → x0 , NhËn xÐt 6.1. Tõ (6.1) vµ (6.2) suy ra: M→ M0 ⇔   y → y0 . §Þnh nghÜa 6.2. Cho X, Y lµ hai tËp hîp c¸c sè thùc. TËp hîp trong R 2 (cßn ®îc gäi lµ miÒn biÕn thiªn cña hai biÕn sè x vµ y) ®îc ký hiÖu vµ x¸c ®Þnh nh sau: D = {(x,y) ∈ R2: x ∈ X, y ∈ Y}. §Þnh nghÜa 6.3. Cho tËp hîp D ⊂ R2 vµ ®iÓm (x0,y0) ∈ D. Víi mçi sè thùc δ > 0 th× l©n cËn δ cña ®iÓm (x0,y0) ®îc ký hiÖu vµ x¸c ®Þnh nh sau: Vδ (x0,y0) = {(x,y) ∈ R2: (x− x0)2 + ( y− y0)2 < δ2}, ⇔ {(x,y) ∈ R2: d[(x0, y0);(x,y) ] < δ}. Hay l©n cËn δ cña ®iÓm (x0,y0) lµ h×nh trßn më cã t©m t¹i ®iÓm (x0,y0) vµ b¸n kÝnh δ. (vÏ h×nh, gi¶i thÝch). §Þnh nghÜa 6.4. Cho tËp hîp D⊂ R2 vµ ®iÓm M0(x0,y0) ∈ D. (i) §iÓm M0 ®îc gäi lµ ®iÓm trong cña D nÕu tån t¹i sè δ > 0 sao cho: 1
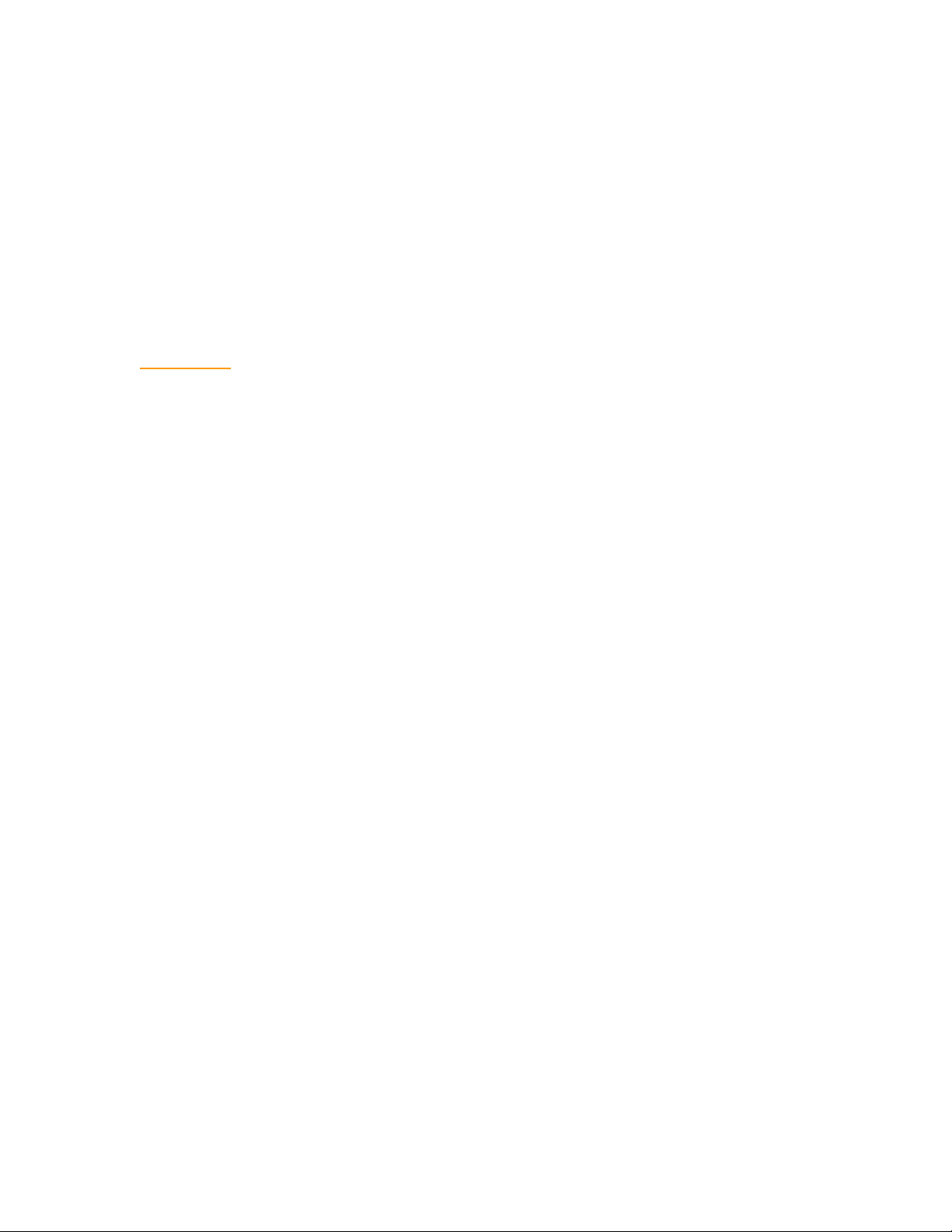
Vδ (x0,y0) ⊂ D. TËp D ®îc gäi lµ tËp më nÕu mäi ®iÓm cña nã ®Òu lµ ®iÓm trong. (ii) §iÓm M0 ®îc gäi lµ ®iÓm biªn cña D nÕu mäi l©n cËn Vδ (x0,y0) ®Òu võa chøa c¸c ®iÓm thuéc D, võa chøa c¸c ®iÓm kh«ng thuéc D. TËp hîp tÊt c¶ c¸c ®iÓm biªn cña tËp D ®îc gäi lµ biªn cña tËp D vµ ký hiÖu lµ:∂ D.(vÏ h×nh). (iii) TËp D ®îc gäi lµ tËp ®ãng nÕu D chøa mäi ®iÓm biªn cña nã. VÝ dô 6.1. VÏ miÒn biÕn thiªn vµ x¸c ®Þnh biªn cña nã cho c¸c trêng hîp sau: a) D = {(x,y) ∈ R2: x ∈ [0; 3], y ∈ (2; 4]}. b) D = {(x,y) ∈ R2: x ∈ [0; 3], y ∈ [2; 4]∪{6}}. c) D = {(x,y) ∈ R2: x − y = 0}. d) D = {(x,y) ∈ R2: x2 + y2 < 4}. 6.1.2. §Þnh nghÜa hµm hai biÕn sè. §Þnh nghÜa 6.5. Cho miÒn biÕn thiªn D. NÕu øng víi mçi ®iÓm (x,y) ∈ D, theo mét quy luËt nµo ®ã cho ta mét gi¸ trÞ x¸c ®Þnh (vµ duy nhÊt) z ∈ R th× z ®îc gäi lµ hµm cña hai biÕn sè x vµ y. Ng êi ta ký hiÖu z lµ hµm cña hai biÕn sè x vµ y lµ bëi: z = f(x,y), z = h(x,y),... Cho hµm hai biÕn sè z = f(x,y). ∗ TËp hîp tÊt c¶ c¸c ®iÓm (x,y) sao cho f(x,y) cã nghÜa ®îc gäi lµ miÒn x¸c ®Þnh cña hµm hai biÕn z = f(x,y). ∗ NÕu (x0,y0) lµ ®iÓm thuéc miÒn x¸c ®Þnh cña hµm z =f(x,y) th× f(x0,y0) ®îc gäi lµ gi¸ trÞ riªng cña hµm z = f(x,y) t¹i ®iÓm (x0,y0). ∗ TËp hîp tÊt c¶ c¸c gi¸ trÞ f(x,y), trong ®ã (x,y) lµ ®iÓm thuéc miÒn x¸c ®Þnh cña hµm z = f(x,y) ®îc gäi lµ miÒn gi¸ trÞ cña hµm z = f(x,y). ∗ TËp hîp tÊt c¶ c¸c ®iÓm (x,y, f(x,y)) trong ®ã (x,y) lµ ®iÓm thuéc miÒn x¸c ®Þnh cña hµm z = f(x,y) ®îc gäi lµ ®å thÞ cña hµm z = f(x,y). 2
4 − x 2 − y 2 . Khi ®ã, VÝ dô 6.2. Cho hµm hai biÕn sè z = ∗ MiÒn x¸c ®Þnh cña hµm sè lµ: D = {(x,y) ∈ R2: x2 + y2 ≤ 4}. Hay miÒn x¸c ®Þnh cña hµm sè lµ h×nh trßn cã t©m t¹i ®iÓm (0,0), b¸n kÝnh b»ng 2, kÓ c¶ biªn (∂ D lµ ®êng trßn cã t©m t¹i ®iÓm (0,0), b¸n kÝnh b»ng 2). ∗ MiÒn gi¸ trÞ cña hµm sè lµ: [0,2]. ∗ §å thÞ cña hµm sè lµ nöa mÆt cÇu (n»m phÝa trªn mÆt ph¼ng z = 0) cã t©m t¹i ®iÓm (0,0), b¸n kÝnh b»ng 2. 6.2. Giíi h¹n vµ sù liªn tôc cña hµm hai biÕn sè 6.2.1. Giíi h¹n cña hµm hai biÕn sè. §Þnh nghÜa 6.7. Cho ®iÓm M0(x0,y0) ∈ R2 vµ hµm z =f(x,y) = f(M) x¸c ®Þnh trong mét l©n cËn V0 nµo ®ã cña M0 (cã thÓ trõ ®iÓm M0). H»ng sè b ®îc gäi lµ giíi h¹n cña hµm z =f(x,y) = f(M) khi M → M0 nÕu víi mäi ε > 0, tån t¹i δ > 0 sao cho víi mäi M(x,y) ∈ Vδ (x0,y0) = Vδ (M0) th× | f(x,y) −b| < ε . Khi ®ã, ta viÕt: f ( x , y) = b . lim f ( M ) = b hay lim ( x , y ) →( x 0 , y0 ) M →M0 ⇔ (∀ε > 0),(∃ Vδ (x0,y0):∀(x,y) ∈Vδ (x0,y0)) ⇒ | f(x,y)−b| < ε . 3
xy = 0. VÝ dô 6.3. Chøng minh r»ng : ( x , ylim 0 ,0) ) →( 2 2 x +y 1 Gi¶i. Víi mçi ε > 0 cho tríc, chän δ = ε. Víi (x, y) ≠ (0, 0) ta cã: 2 xy xy 1 xy ( x − 0) + ( y − 0) = d ( x , y ) ; ( 0 , 0 )  < ε 2 2 x 2 + y2 ≤ −0 = 2  x2 + y2 2 xy x 2 + y2 1 VËy (∀ε > 0),(∃ δ = ε> 0:∀(x,y) ∈Vδ (x0,y0)) ⇒ | f(x,y)−b| < ε.(®pcm) 2 Chó ý 6.1. (i) Kh¸i niÖm giíi h¹n v« h¹n cña hµm hai biÕn sè còng ® îc ®Þnh nghÜa t¬ng tù nh ®èi víi hµm mét biÕn. (ii) C¸c kÕt qu¶ vÒ giíi h¹n cña tæng, hiÖu, tÝch, th ¬ng ®èi víi hµm mét biÕn còng ®óng cho hµm hai biÕn. NhËn xÐt 6.2. (i) §Þnh nghÜa 6.7 cßn ®îc ph¸t biÓu díi d¹ng: “H»ng sè b ®îc gäi lµ giíi h¹n cña hµm f(x,y) khi (x,y) → (x0,y0) nÕu víi mäi d·y ®iÓm V0\{(x0,y0)} ∋ (xn,yn) → (x0,y0) ®Òu cã: nlim f ( x n , y n ) = b”, trong ®ã f(x,y); (x0,y0) ; V0 t¬ng tù nh trong ®Þnh nghÜa →+∞ 6.7. (ii) Qua phÇn (i) cña nhËn xÐt nµy ta thÊy (t¬ng tù nh ®èi víi hµm mét biÕn): §Ó chøng minh giíi h¹n cña hµm hai biÕn f(M) khi M → M0 kh«ng tån t¹i, ta chØ cÇn chØ ra hai d·y Mn, Nn cïng → M0 (Mn, Nn ≠ M0) khi n → + ∞ mµ f(Mn) → b, f(Nn) → k vµ b ≠ k. xy lim VÝ dô 6.4. Chøng minh r»ng kh«ng tån t¹i. ( x , y ) → ( 0 , 0) x 2 + y 2  1 1 1 1  Gi¶i. Chän Mn =  , ÷, Nn =  , 2 ÷. n n  n n  4
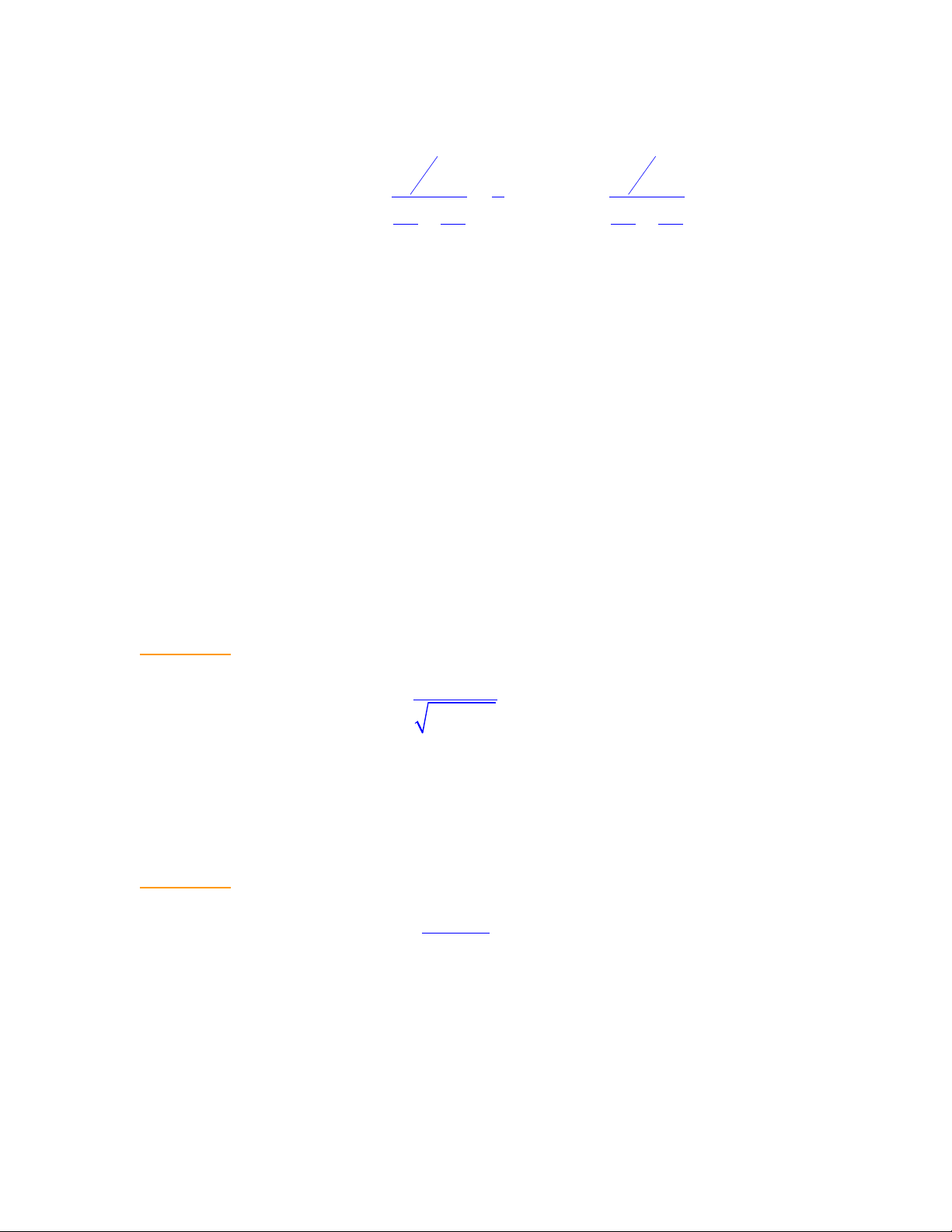
Th× Mn, Nn cïng → M0 =(0,0) khi n → + ∞ . Mµ: 1 13 1 2 lim f ( M n ) = lim f ( N n ) . n n = lim = ≠ 0 = lim n →+∞ 1 1 n →+∞ 1 1 n →+∞ 2 n →+∞ + + n2 n2 n2 n4 ¸p dông kÕt qu¶ cña nhËn xÐt 6.2 phÇn (ii) ta cã ®iÒu ph¶i chøng minh. 6.2.2. Sù liªn tôc cña hµm hai biÕn sè. §Þnh nghÜa 6.8. Cho hµm z = f(x,y) x¸c ®Þnh trªn miÒn D, ®iÓm M0∈D. hµm z = f(x,y) ®îc gäi lµ liªn tôc t¹i M0 nÕu: f ( x , y ) = f ( x 0 , y0 ) . lim ( , y ) →( x 0 , y0 ) NÕu D lµ tËp ®ãng vµ M0∈ ∂ D th× trong giíi h¹n trªn ta ph¶i hiÓu theo nghÜa: M(x,y) → M0 víi M∈ D. Hµm z = f(x,y) ®îc gäi lµ liªn tôc trªn miÒn D nÕu nã liªn tôc t¹i mäi ®iÓm thuéc D. VÝ dô 6.5. XÐt sù liªn tôc t¹i ®iÓm (0,0) cña hµm:  xy k h i ( x , y ) ≠ ( 0 , 0) , 2 x + y2 f(x,y) =   0 k h i ( x , y ) = ( 0 , 0) .  Gi¶i. Tõ kÕt qu¶ cña vÝ dô 6.3 vµ tõ ®Þnh nghÜa 6.8 suy ra hµm sè ®· cho liªn tôc t¹i ®iÓm (0,0). VÝ dô 6.6. XÐt sù liªn tôc t¹i ®iÓm (0,0) cña hµm:  xy k h i ( x , y ) ≠ ( 0, 0) , 2 x + y2 f(x,y) =   0 k h i ( x , y ) = ( 0, 0) .  Gi¶i. Tõ kÕt qu¶ cña vÝ dô 6.4 vµ tõ ®Þnh nghÜa 6.8 suy ra hµm sè ®· cho kh«ng liªn tôc t¹i ®iÓm (0,0). 5
NhËn xÐt 6.3. (i) Hµm hai biÕn sè liªn tôc còng cã c¸c tÝnh chÊt nh hµm mét biÕn liªn tôc. (ii) Cho hµm z = f(x,y) vµ M0 nh trong ®Þnh nghÜa 6.8. Víi mçi ®iÓm M(x0+∆ x,y0+∆ y) ∈ D, ®Æt ∆ f x0,y0) = f(x0+∆ x,y0+∆ y) − f(x0,y0). Khi ®ã, ®Þnh ( nghÜa 6.8 cã thÓ ph¸t biÓu nh sau: Hµm z = f(x,y) liªn tôc t¹i ®iÓm M0 nÕu nã x¸c ®Þnh t¹i ®iÓm ®ã ®ång thêi ∆ f x0,y0) → 0 khi ∆ x → 0, ∆ y → 0. ( 6.3. §¹o hµm riªng, vi ph©n riªng 6.3.1. §¹o hµm riªng, vi ph©n riªng. Cho hµm z = f(x,y) x¸c ®Þnh trªnmiÒn D, ®iÓm M0(x0,y0) ∈ D. Cè ®Þnh y = y0 th× z = f(x,y) = f(x,y0) lµ hµm sè mét biÕn. Víi mçi ®iÓm M(x0+∆ x,y0) ∈ D. §Æt ∆ xf x0,y0) = f(x0+∆ x,y0) − f(x0,y0) vµ gäi lµ sè gia riªng cña hµm z = f(x,y) t¹i ®iÓm ( (x0,y0) theo biÕn x. §Þnh nghÜa 6.9. NÕu hµm f(x,y0) cã ®¹o hµm t¹i ®iÓm x0 th× ®¹o hµm ®ã ®îc gäi lµ ®¹o hµm riªng cÊp 1 cña hµm z = f(x,y) t¹i ®iÓm (x0,y0) theo biÕn x vµ ký hiÖu lµ: ∂f ∂z f′ x(x0,y0) hay (x0,y0) hay (x0,y0). ∂x ∂x f ( x 0 + ∆ x , y 0 ) − f ( x 0 , y0 ) ∂f (x0,y0) = lim VËy . ∆x ∂x ∆ x →0 T¬ng tù, ®¹o hµm riªng cÊp 1 cña hµm z = f(x,y) t¹i ®iÓm (x0,y0) theo biÕn y ®îc ký hiÖu vµ x¸c ®Þnh nh sau: ∂f ∂z f′ y(x0,y0) hay (x0,y0) hay (x ,y ). ∂y 0 0 ∂y f ( x0 , y0 + ∆ y ) − f ( x 0 , y0 ) ∂f (x0,y0) = lim VËy . ∂y ∆y ∆ y →0 6
NhËn xÐt 6.4. Khi tÝnh ®¹o hµm riªng theo mét biÕn nµo ®ã cña hµm z = f(x,y) t¹i ®iÓm (x0,y0), ta coi hµm f(x,y) chØ phô thuéc vµo mét biÕn ®ã biÕn cßn l¹i kh«ng ®æi, råi ¸p dông c¸c quy t¾c tÝnh ®¹o hµm cña hµm mét biÕn ®Ó tÝnh. §Þnh nghÜa 6.10. NÕu hµm z = f(x,y) cã ®¹o hµm riªng cÊp 1 theo x t¹i ®iÓm (x0,y0) th× vi ph©n riªng cÊp 1 cña hµm z = f(x,y) theo x t¹i ®iÓm (x0,y0) ®îc ký hiÖu vµ x¸c ®Þnh nh sau: dfx(x0,y0) = f′ x(x0,y0)∆ x hay dzx(x0,y0) = z′ x(x0,y0)∆ x. T¬ng tù, nÕu hµm z = f(x,y) cã ®¹o hµm riªng cÊp 1 theo y t¹i ®iÓm (x0,y0) th× vi ph©n riªng cÊp 1 cña hµm z = f(x,y) theo y t¹i ®iÓm (x0,y0) ®îc ký hiÖu vµ x¸c ®Þnh nh sau: dfy(x0,y0) = f′ y(x0,y0)∆ y hay dzy(x0,y0) = z′ y(x0,y0)∆ y. VÝ dô 6.7. TÝnh c¸c ®¹o hµm riªng vµ vi ph©n riªng cña c¸c hµm sè sau: 1 a) z =yax (0 < a ≠ 1), (y ≠ 0). b) z =x3arctg y Gi¶i. a) z = yax (0 < a ≠ 1) ⇒ z′ x(x,y) = yaxlna, dzx(x,y) = z′ x(x,y)∆ x = yaxlna∆ x. z′ y(x,y) = ax, dzy(x,y) = z′ y(x,y)∆ y = ax∆ y. 1 1 1 (y ≠ 0). ⇒ z′ x(x,y) =3 x2arctg , dzx(x,y) = 3 x2arctg ∆ x. b) z =x3arctg y y y −x3 −x3 z′ y(x,y) = ∆ y. , dzy(x,y) = 1 + y2 1 + y2 6.3.2. Vi ph©n toµn phÇn. Cho hµm z = f(x,y) x¸c ®Þnh trªn miÒn D, ®iÓm M0(x0,y0) ∈ D. Víi mçi ®iÓm M(x0+∆ x,y0+∆ y) ∈ D. §Æt ∆ xf x0,y0) = f(x0+∆ x,y0) − f(x0,y0) vµ gäi lµ sè gia toµn ( phÇn cña hµm z = f(x,y) t¹i ®iÓm (x0,y0). 7
§Þnh nghÜa 6.11. NÕu sè gia toµn phÇn cña hµm z = f(x,y) t¹i ®iÓm (x0,y0) biÓu diÔn ®îc díi d¹ng: ∆ xf x0,y0) = A∆ x + B∆ y + α∆ x + β∆ y , ( trong ®ã A, B lµ c¸c h»ng sè chØ phô thuéc vµo x 0, y0 , cßn α vµ β dÇn tíi 0 khi M → M0 (hay khi ∆ x →0, ∆ y →0). Th× ta nãi r»ng hµm z = f(x,y) kh¶ vi t¹i ®iÓm (x0, y0) vµ biÓu thøc A∆ x + B∆ y ®îc gäi lµ vi ph©n toµn phÇn cña hµm z = f(x,y) t¹i ®iÓm (x0,y0), ký hiÖu lµ dz x0,y0) hoÆc df x0,y0). ( ( Hµm z = f(x,y) ®îc gäi lµ kh¶ vi trªn miÒn D nÕu nã kh¶ vi t¹i mäi ®iÓm thuéc D. §Þnh lý 6.1. NÕu hµm z = f(x,y) cã c¸c ®¹o hµm riªng trong mét l©n cËn nµo ®ã cña ®iÓm (x0,y0) vµ c¸c ®¹o hµm riªng cña nã liªn tôc t¹i (x0,y0) th× hµm z = f(x,y) kh¶ vi t¹i (x0,y0) vµ: df x0,y0) = f′ x(x0,y0)∆ x + f′ y(x0,y0)∆ y. ( Chó ý 6.2. Còng nh ®èi víi hµm mét biÕn ta cã: dx =∆ x , dy =∆ y. Do ®ã, nÕu hµm z = f(x,y) tho¶ m·n ®iÒu kiÖn cña ®Þnh lý 6.1 th× df x0,y0) = f′ x(x0,y0)dx + f′ y(x0,y0)dy. ( VÝ dô 6.8. TÝnh vi ph©n toµn phÇn (nÕu cã) cña hµm z = yax (víi 0
NÕu hµm z = f(x,y) tho¶ m·n ®iÒu kiÖn cña ®Þnh lý 6.1 vµ ∆ x , ∆ y ®ñ nhá th×: ∆ xf x0,y0) ≅ f′ x(x0,y0)∆ x + f′ y(x0,y0)∆ y. ( C«ng thøc nµy ®îc sö dông ®Ó tÝnh gÇn ®óng gi¸ trÞ cña hµm sè hai biÕn t¹i ®iÓm (x0,y0). VÝ dô 6.9. TÝnh gÇn ®óng sè: 8,25 sin 50o. π π Gi¶i. §Æt f(x,y) = x3sin y; (x0,y0) = (2, ); ∆ x = 0,25, ∆ y = − . 6 36 π Th× f(x,y) cã c¸c ®¹o hµm riªng trªn R2 do ®ã cã ®¹o hµm riªng t¹i (2, ) ; 6 π f′ x(x,y) = 3 x2 sin y, f′ y(x,y) = x3 cos y lµ nh÷ng hµm liªn tôc t¹i (2, ). Theo nhËn xÐt 6 6.5 ta cã: π π π (2, ) ≅ f′ x(2, )∆ x + f′ y(2, )∆ y. ∆ x f 6 6 6 ≅ 6 ∆ x + 4 3 ∆ y. NhËn xÐt 6.6. §èi víi hµm mét biÕn y =f (x) mµ t¹i ®iÓm x0 hµm sè cã ®¹o hµm vµ f′ (x0) h÷u h¹n th×:∆ f x0) = df x0) + o(∆ x), trong ®ã o(∆ x) lµ VCB bËc cao h¬n ∆ x ( ( khi ∆ x tiÕn dÇn tíi 0. Tuy nhiªn, ®èi víi hµm hai biÕn th× kÕt qu¶ nµy kh«ng ®óng. Ch¼ng h¹n ®èi víi hµm  xy k h i ( x , y ) ≠ ( 0 , 0) 2 x + y2 f(x,y) =  t¹i ®iÓm (0,0).  0 k h i ( x , y ) = ( 0, 0)  6.3.3. §¹o hµm riªng cÊp hai. 9
§Þnh nghÜa 6.12. Cho D ⊂ R2; ®iÓm M0(x0,y0) ∈ D; hµm z = f(x,y) x¸c ®Þnh trªn miÒn D vµ cã c¸c ®¹o hµm riªng f ′ x(.,.), f′ y(.,.) trong mét l©n cËnV0 nµo ®ã cña (x0,y0), V0 ⊂ D. Th× f′ x(x,y), f′ y(x,y) lµ c¸c hµm hai biÕn sè x¸c ®Þnh trªn V0. NÕu hµm f′ x(x,y) cã ®¹o hµm riªng theo x t¹i ®iÓm (x0,y0) th× ta nãi r»ng hµm z = f(x,y) cã ®¹o hµm riªng cÊp 2, hai lÇn theo x t¹i ®iÓm (x0,y0). §¹o hµm riªng hai lÇn theo x ∂2 f cña hµm z = f(x,y) t¹i ®iÓm (x0,y0) ®îc ký hiÖu lµ f′ ′ xx(x0,y0) hoÆc 2 ( x0 , y0 ) . VËy: ∂x ∂  ∂f ( .,.)  ∂2 f f′ ′ xx(x0,y0) = 2 ( x0 , y0 ) =   . ∂x  ∂x  ( x0 , y0 ) ∂x B»ng c¸ch t¬ng tù, ®¹o hµm riªng cÊp 2, hai lÇn theo y (theo x, theo y vµ theo y, theo x) cña hµm z = f(x,y) t¹i ®iÓm (x0,y0) t¬ng øng ®îc ký hiÖu vµ x¸c ®Þnh nh sau: ∂  ∂f ( .,.)  ∂2 f f′ ′ yy(x0,y0) = 2 ( x0 , y0 ) =   . ∂y  ∂y  ( x0 , y0 ) ∂y ∂  ∂f ( .,.)  ∂2 f = f′ ′ yx(x0,y0) =   . ∂x ∂y ( x0 , y0 ) ∂y  ∂x  ( x 0 , y0 ) ∂  ∂f ( .,.)  ∂2 f x 0 ,y 0 ) = f′ ′ xy(x0,y0) =   . ∂y ∂x ( ∂x  ∂y  ( x 0 , y0 ) Chó ý 6.3. §Ó cho gän, chóng ta thêng viÕt f′ ′ thay cho f′ ′ xy(x,y), f′ y thay cho xy f′ y(x,y), c¸c ký hiÖu kh¸c ta còng lµm t¬ng tù. VÝ dô 6.10. TÝnh c¸c ®¹o hµm riªng ®Õn cÊp hai (nÕu cã) cña hµm sè : z = x2y − sin xy. z′ x = 2xy− y cos xy, z′ y = x2 −x cos xy, Gi¶i. z′ ′ = 2y + y2sin xy, z′ ′ = x2 cos xy, z′ ′ = z′ ′ = 2x+ xysin xy− y cos xy. xx yy xy yx 10
NhËn xÐt 6.8. Theo kÕt qu¶ cña vÝ dô 6.10 ta cã z′ ′ = z′ ′ yx. VÊn ®Ò ®Æt ra lµ xy ®iÒu ®ã cßn ®óng n÷a kh«ng ®èi víi hµm hai biÕn kh¸c? Chóng ta thõa nhËn ®Þnh lý sau. §Þnh lý 6.2 (Schwarz). NÕu trong l©n cËn V0 cña ®iÓm (x0,y0) hµm z = f(x,y) cã c¸c ®¹o hµm riªng z′ ′ , z′ ′ lµ nh÷ng hµm liªn tôc t¹i (x0,y0) th×: xy yx f′ ′ xy(x0,y0) = f′ ′ yx(x0,y0). 6.4. Cùc trÞ cña hµm hai biÕn sè §Þnh nghÜa 6.13. Cho D ⊂ R2; ®iÓm M0(x0,y0) ∈ D; hµm z = f(x,y) x¸c ®Þnh trªn miÒn D. (i) NÕu tån t¹i δ > 0 sao cho: f(x,y) − f(x0,y0) ≤ 0 (∀(x,y) ∈ D∩Vδ(x0,y0)\{(x0,y0)}), th× ta nãi r»ng hµm z = f(x,y) ®¹t cùc ®¹i ®Þa ph¬ng t¹i (x0,y0). (ii) NÕu tån t¹i δ > 0 sao cho: f(x,y) − f(x0,y0) ≥ 0 (∀(x,y) ∈ D∩Vδ(x0,y0)\{(x0,y0)}), th× ta nãi r»ng hµm z = f(x,y) ®¹t cùc tiÓu ®Þa ph¬ng t¹i (x0,y0). VÝ dô 6.11. Hµm z = f(x,y) = | x|+| y| ®¹t cùc tiÓu ®Þa ph¬ng t¹i (0,0) v×: f(x,y) = | x|+| y| x¸c ®Þnh trªn R2; f(x,y) − f(0,0) = | x|+| y| − 0 > 0 (∀(x,y) ∈ R2∩ V2(0,0)\{(0,0)}). VÝ dô 6.12. Hµm z = f(x,y) = cos (x+ y) ®¹t cùc ®¹i ®Þa ph¬ng t¹i (0,0) v×: f(x,y) = cos (x+ y) x¸c ®Þnh trªn R2; V1 f(x,y) − f(0,0) = cos (x+ y) − 0 < 0 (∀(x,y) ∈ R2∩ (0,0)\{(0,0)}). 2 NhËn xÐt 6.9. Ta dÔ dµng chøng minh ®îc hµm f(x,y) = | x|+| y| kh«ng cã c¸c ®¹o hµm riªng t¹i ®iÓm (0,0) vµ hµm h(x,y) = cos(x+ y) cã c¸c ®¹o hµm riªng t¹i ®iÓm (0,0), h′ x(0,0) = h′ y(0,0) = 0 . KÕt hîp víi kÕt qu¶ cña c¸c vÝ dô 6.11 vµ 6.12, liÖu ta 11
cã thÓ ®i ®Õn kÕt luËn ®èi víi hµm hai biÕn t ¬ng tù nh ®èi víi hµm mét biÕn lµ: “Mét hµm sè chØ ®¹t cùc trÞ t¹i nh÷ng ®iÓm mµ t¹i ®ã hµm sè kh«ng cã ®¹o hµm hoÆc t¹i ®ã cã ®¹o hµm th× ®¹o hµm cña hµm sè t¹i ®iÓm ®ã b»ng 0 ”hay kh«ng? §Þnh lý 6.3 sau ®©y kh¼ng ®Þnh ®iÒu ®ã. §Þnh lý 6.3. NÕu hµm z = f(x,y) ®¹t cùc trÞ t¹i ®iÓm (x0,y0) vµ t¹i ®ã hµm sè cã c¸c ®¹o hµm riªng cÊp 1 theo x, theo y. Th× c¸c ®¹o hµm riªng cÊp 1 cña hµm f (x,y) theo x, theo y t¹i (x0,y0) ®Òu b»ng 0. Tøc lµ: f′ x(x0,y0) = f′ y(x0,y0) = 0. §Þnh nghÜa 6.14. Cho D ⊂ R2; ®iÓm M0(x0,y0) ∈ D; hµm z = f(x,y) x¸c ®Þnh trªn miÒn D. NÕu t¹i (x0,y0) hµm sè cã c¸c ®¹o hµm riªng cÊp 1 theo x, theo y vµ c¸c ®¹o hµm riªng cÊp 1 cña hµm f(x,y) theo x, theo y t¹i (x0,y0) ®Òu b»ng 0. Th× ®iÓm (x0,y0) ®îc gäi lµ ®iÓm dõng cña hµm z = f(x,y). TËp hîp c¸c ®iÓm dõng cña hµm z = f (x,y) vµ c¸c ®iÓm mµ hµm f (x,y) kh«ng cã c¸c ®¹o hµm riªng cÊp 1 theo x, theo y ® îc gäi lµ tËp hîp c¸c ®iÓm tíi h¹n cña hµm z = f(x,y). NhËn xÐt 6.10. Tõ ®Þnh lý 6.3 ta ®i ®Õn kÕt luËn lµ chØ ph¶i t×m cùc trÞ cña hµm hai biÕn t¹i nh÷ng ®iÓm tíi h¹n cña hµm sè ®ã. §Þnh lý 6.4. Cho D ⊂ R2; ®iÓm M0(x0,y0) ∈ D; hµm z = f(x,y) x¸c ®Þnh trªn miÒn D. Gi¶ sö hµm f(x,y) cã c¸c ®¹o hµm riªng ®Õn cÊp 2 (theo c¸c biÕn) vµ lµ c¸c hµm liªn tôc trong mét l©n cËn nµo ®ã cña ®iÓm (x0,y0). §ång thêi (x0,y0) lµ ®iÓm dõng cña hµm f(x,y). Khi ®ã: (i) NÕu B2− AC < 0 th× f(x,y) ®¹t cùc trÞ t¹i (x0,y0) (cùc tiÓu nÕu A > 0, cùc ®¹i nÕu A < 0). (ii) NÕu B2− AC = 0 th× cha kÕt luËn ®îc t¹i (x0,y0) hµm sè cã ®¹t cùc trÞ hay kh«ng. Trong ®ã, A =f′ ′ xx(x0,y0), B =f′ ′ xy(x0,y0), C =f′ ′ yy(x0,y0). VÝ dô 6.13. T×m cùc trÞ ®Þa ph¬ng cña c¸c hµm sè sau: 12
a) z = x3 + 2y3 − 3x − 6y; b) z = x2 + y2 + xy − 3x − 6y. Gi¶i. a) z = x3 + 2y3 − 3x − 6y. Hµm sè x¸c ®Þnh vµ cã c¸c ®¹o hµm riªng ®Õn cÊp 2 trªn R2. z′ x = 3x2 − 3, z′ y = 6y2 − 6 ⇒ TËp c¸c ®iÓm dõng cña hµm sè lµ: M1(−1,−1), M2(−1,1), M3(1,−1), M4(1,1). z′ ′ = 6x, z′ ′ = 12y, z′ ′ = z′ ′ = 0. xx yy xy yx T¹i ®iÓm M1(−1,−1). cã: A = −6 < 0, B = 0, C = −12 ⇒ B2 − AC = − 72. VËy hµm sè ®¹t cùc ®¹i ®Þa ph¬ng t¹i M1 vµ zmax = z(−1, −1) = −6. T¹i ®iÓm M2(−1,1). cã: A = −6 < 0, B = 0, C = 12 ⇒ B2 − AC = 72. VËy hµm sè kh«ng ®¹t cùc trÞ t¹i M2. T¹i ®iÓm M3(1,−1). cã: A = 6 > 0, B = 0, C = −12 ⇒ B2 − AC = 72. VËy hµm sè kh«ng ®¹t cùc trÞ t¹i M3. T¹i ®iÓm M4(1,1). cã: A = 6 > 0, B = 0, C = −12 ⇒ B2 − AC = − 72. VËy hµm sè ®Æt cùc tiÓu ®Þa ph¬ng t¹i M4 vµ zmin = z(1,1) = −6. b) z = x2 + y2 + xy − 3x − 6y. Hµm sè x¸c ®Þnh vµ cã c¸c ®¹o hµm riªng ®Õn cÊp 2 trªn R2. z′ x = 2x + y − 3, z′ y = 2y + x − 6 ⇒ TËp c¸c ®iÓm dõng cña hµm sè lµ: M0(0,3). VËy hµm sè chØ cã thÓ ®¹t cùc trÞ ®Þa ph¬ng t¹i M0. z′ ′ = 2, z′ ′ = 2, z′ ′ = z′ ′ = 1. xx yy xy yx T¹i ®iÓm M0(0,3). cã: A = 2 > 0, B = 1, C = 2 ⇒ B2 − AC = − 3. VËy hµm sè ®Æt cùc tiÓu ®Þa ph¬ng t¹i M4 vµ zmin = z(0,3) = −9. C©u hái «n tËp ch¬ng 4. C©u 1: §Þnh nghÜa miÒn biÕn thiªn cña hai biÕn sè. §Þnh nghÜa hµm sè hai biÕn sè. C©u 2: §Þnh nghÜa ®¹o hµm riªng, vi ph©n riªng, vi ph©n toµn phÇn cña hµm hai biÕn sè. 13
C©u 3: §Þnh nghÜa cùc trÞ cña hµm hai biÕn sè. C¸ch t×m cùc trÞ cña hµm hai biÕn sè. 14