Trang 23
CHUYÊN ĐỀ VẬ T LÝ 12 LUYỆ N THI TN THPT –CAO ĐẲ NG –ĐẠ I HỌ C
0937 944 688 Email: tringuyenlqd@gmail.com Website: violet.vn/tringuyenlqd
CHƯ Ơ NG II
DAO ĐỘ NG CƠ HỌ C
CHỦ ĐỀ 5
ĐẠ I CƯ Ơ NG VỀ DAO ĐỘ NG ĐIỀ U HÒA
A. TÓM TẮ T KIẾ N THỨ C CƠ BẢ N
I. DAO ĐỘ NG TUẦ N HOÀN
1. Đị nh nghĩa: là dao độ ng mà trạ ng thái chuyể n độ ng củ a vậ t đượ c lặ p lạ i như cũ sau nhữ ng khoả ng thờ i gian
bằ ng nhau xác đị nh.
2. Chu kì, tầ n số củ a dao độ ng:
+ Chu kì T củ a dao độ ng điề u hòa là khoả ng thờ i gian để thự c hiệ n mộ t dao độ ng toàn phầ n; đơ n vị giây (s.
2t
TN
= =
Vớ i N là số dao độ ng toàn phầ n vậ t thự c hiệ n đượ c trong thờ i gian t.
+ Tầ n số f củ a dao độ ng điề u hòa là số dao độ ng toàn phầ n thự c hiệ n đư ợ c trong mộ t giây; đơ n vị héc Hz.
1
2
N
fT t
= = =
II. DAO ĐỘ NG ĐIỀ U HÒA
1. Đị nh nghĩa: là dao độ ng mà trạ ng thái dao độ ng đượ c mô tả bở i đị nh luậ t dạ ng cosin (hay sin đố i vớ i thờ i gian.
2. Phư ơ ng trình dao độ ng: x = Acos ωt + ϕ.
Các đạ i lượ ng đặ c trư ng củ a dao độ ng điề u hòa
+Li độ x: là độ lệ ch củ a vậ t khỏ i vị trí cân bằ ng
+Biên độ A : là giá trị cự c đạ i củ a li độ , luôn dư ơ ng
+ Pha ban đầ u :xác đị nh li độ x tạ i thờ i điể m ban đầ u t = 0
+Pha củ a dao độ ng ωt + ϕ: xác đ ị nh li độ x củ a dao độ ng tạ i thờ i điể m t.
+ Tầ n số góc :là tố c độ biế n đổ i góc pha. ω=
T
2
= 2πf. Đơ n vị : rad/s
+Biên độ và pha ban đầ u có nhữ ng giá trị khác nhau, tùy thuộ c vào cách
kích thích dao độ ng.
+Tầ n số góc có giá trị xác đị nh (không đổ i đố i vớ i hệ vậ t đ ã cho.
3. Phư ơ ng trình vậ n tố c: v = x’ = -ωAsin ωt + ϕ = ωAcos ωt + ϕ+
2
.
+ Véctơ
v
luôn cùng chiề u vớ i chiề u chuyể n độ ng vậ t chuyể n độ ng theo chiề u d ư ơ ng thì v > 0, theo chiề u âm
thì v < 0.
+ Vậ n tố c củ a vậ t dao độ ng điề u hòa biế n thiên điề u hòa cùng tầ n số như ng sớ m pha hơ n
2
so vớ i vớ i li độ .
+ Vị trí biên x = ±A, v = 0. V ị trí cân bằ ng (x = 0, |v| = v
max
=ωA.
4. Phư ơ ng trình gia tố c: a = - ω
2
Acos ωt + ϕ = ω
2
Acos ωt + ϕ+π = - ω
2
x.
+Véctơ
a
luôn hư ớ ng về vị trí cân bằ ng.
+ Gia tố c củ a vậ t dao độ ng điề u hòa biế n thiên điề u hòa cùng tầ n số như ng ngư ợ c pha vớ i li độ sớ m pha
2
so
vớ i vậ n tố c.
+ Véctơ gia tố c củ a vậ t dao độ ng điề u hòa luôn hư ớ ng về vị trí cân bằ ng, có độ lớ n tỉ lệ vớ i độ lớ n củ a li độ .
5. Vậ t ở VTCB: x = 0; |v|
Max
=ωA; |a|
Min
= 0
Vậ t ở biên: x = ± A; |v|
Min
= 0; |a|
Max
=ω
2
A
6. Sự đổ i chiề u và đổ i dấ u củ a các đạ i lư ợ ng:
+x, a và F đổ i chiề u khi qua VTCB, v đổ i chiề u ở biên.
+ x, a, v, F biế n đổ i cùng T, f và
.
Trang 24
CHUYÊN ĐỀ VẬ T LÝ 12 LUYỆ N THI TN THPT –CAO ĐẲ NG –ĐẠ I HỌ C
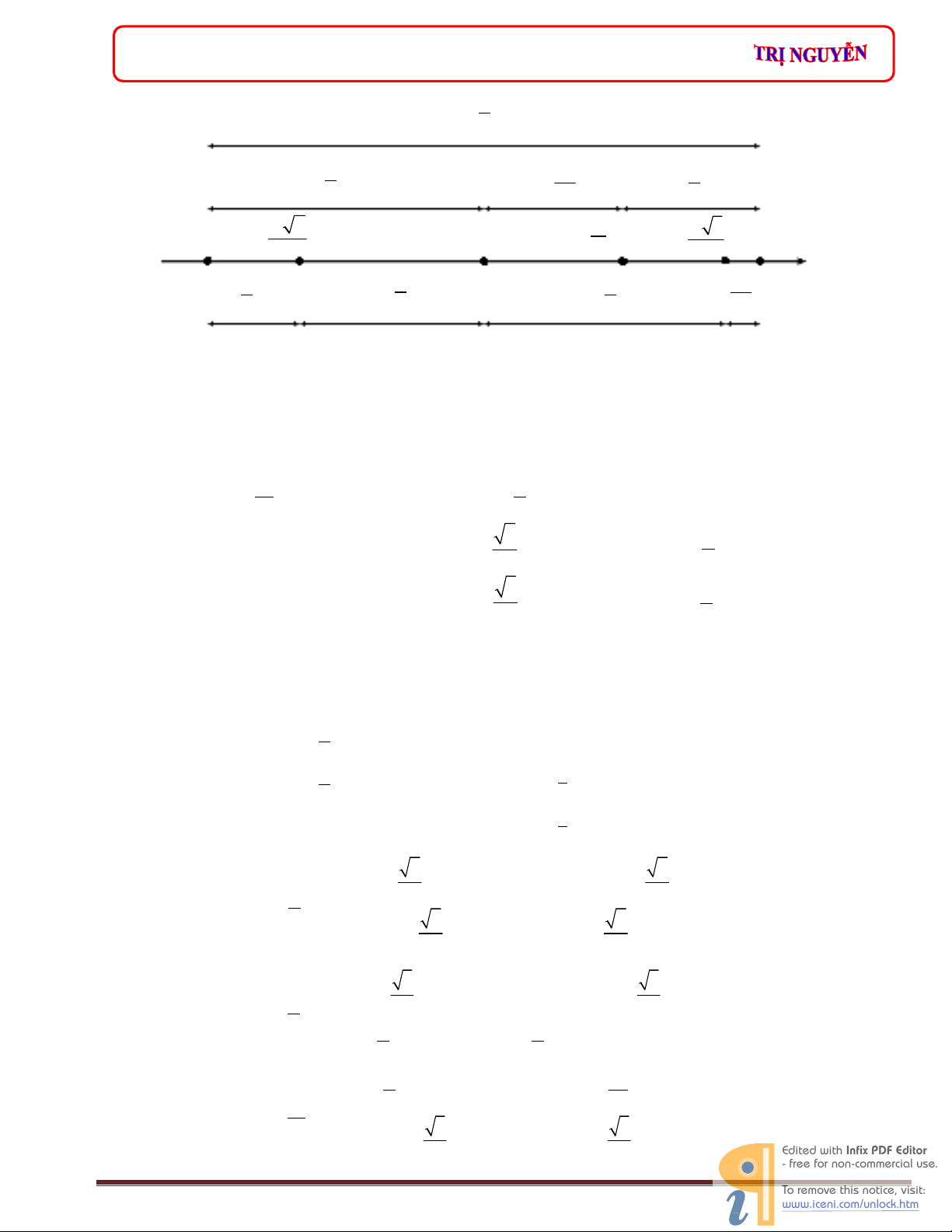
9. Bố n vùng đặ c biệ t cầ n nhớ
a. Vùng 1: x > 0; v < 0; a < 0
⇒Chuyể n độ ng nhanh dầ n theo chiề u (- vì a.v > 0 và th ế
năng giả m, độ ng năng tăng.
b. Vùng 2: x < 0; v < 0; a > 0
⇒Chuyể n độ ng nhanh dầ n theo chiề u (- vì a.v < 0 và th ế
năng tăng, độ ng năng giả m.
c. Vùng 3: x < 0; v > 0; a > 0
⇒Chuyể n độ ng nhanh dầ n theo chiề u (+ v ì a.v > 0 và thế
năng giả m, độ ng năng tăng.
d. Vùng 4: x > 0; v > 0; a < 0
⇒Chuyể n độ ng nhanh dầ n theo chiề u (+ v ì a.v < 0 và thế
năng tăng, độ ng năng giả m.
10. Mố i liên hệ về pha củ a li độ x, vậ n tố c v v à gia tố c a. Theo hình 1.2 ta nhậ n thấ y m ố i liên hệ về pha củ a li
độ (x, vậ n tố c v v à gia tố c (a :
2
v x
= +
và
2
a v x
= + = +
7. Hệ thứ c độ c lậ p:
2
2 2
v
A x
= +
2 2
2
4 2
a v
A
= +
a = -ω
2
x
1
A
a
A
v
2
2
2
=
ω
+
ω
Hay
1
v
a
v
v
max
22
2
2
max
2
=
ω
+
hay
2 2 2 2
max
a v v=ω −
hay
1
a
a
v
v
2
max
2
2
max
2
=+
8. Cơ năng:
2 2 2
đ
1 1
W = W + W 2 2
t
m A k A
= =
Vớ i
2 2 2 2 2
đ
1 1
Wsin W s i n
2 2
m v m A t t
= = + = +
2 2 2 2 2 2
1 1
W W s
2 2
t
m x m A c o s tc o t
= = + = +
Chú ý: + Tìm x hoặ c v khi
đ
W = n W
t
ta làm như sau:
•Tọ a độ x :
2 2
1 1
1
2 2 1
A
kA nkx xn
= + ⇒ =± +
•Vậ n tố c v :
2 2
2 2
2
1 1 1
. .
2 2 1
nmv nkv n
kA kA v A
n n n
+ +
= ⇔ = ⇒ =± +
+ Tìm x hoặ c v khi
đ
W = n W
t
ta làm như sau:
•Tọ a độ x :
2 2
1 1 1
2 2 1
n n
kA kx x A
n n
+
= ⇒ =± +
•Vậ n tố c v :
2 2
2 2
2
11 . 1 .
2 2 1
mv kv A
kA nkA n v n
= + ⇔ = + ⇒ =± +
9. Dao độ ng điề u hoà có tầ n số góc làω, tầ n số f, chu kỳ T. Thìđộ ng năng và thế năng biế n thiên vớ i tầ n số góc 2ω,
tầ n số 2f, chu kỳ T/2. Độ ng năng và thế năng biế n thiên cùng biên độ , cùng tầ n số như ng ngư ơ c pha nhau.
10. Độ ng năng và thế năng trung bình trong thờ i gian nT/2 n ∈N
*
, T là chu kỳ dao độ ng l à:
22
W1
2 4 m A
=
11. Chiề u dài quỹ đạ o: 2A
12. Quãng đư ờ ng đi trong 1 chu kỳ luôn là 4A; trong 1/2 chu kỳ luôn là 2A
Quãng đư ờ ng đi trong l/4 chu kỳ là A khi vậ t đi từ VTCB đế n vị trí biên hoặ c ngư ợ c lạ i
Thờ i gian vậ t đi đư ợ c nhữ ng quãng đư ờ ng đặ c biệ t:
3
x
4
1
ϕ
v
ϕ
x
ϕ
a
2
a
O
Trang 25
CHUYÊN ĐỀ VẬ T LÝ 12 LUYỆ N THI TN THPT –CAO ĐẲ NG –ĐẠ I HỌ C
13. Thờ i gian, quãng đư ờ ng, tố c độ trung bình
a. Thờ i gian: Giả i phư ơ ng trình
c o s
i i
x A t
= +
tìm
i
t
Chú ý:
Gọ i O là trung điể m củ a quỹ đạ o CD và M là trung điể m củ a OD; thờ i gian đi từ O đế n M là
=12
OM
T
t
, thờ i gian đi từ M đế n D là
6
MD
T
t=
.
Từ vị trí cân bằ ng
0x=
ra vị trí
2
2
x A=±
m ấ t khoả ng thờ i gian
8
T
t=
.
Từ vị trí cân bằ ng
0x=
ra vị trí
3
2
x A=±
m ấ t khoả ng thờ i gian
6
T
t=
.
Chuyể n độ ng từ O đế n D là chuyể n độ ng chậ m dầ n đề u
0 ;a v a v<↑ ↓
, chuy ể n độ ng từ D đế n O là
chuyể n độ ng nhanh dầ n đề u
0 ;a v a v>↑ ↑
Vậ n tố c cự c đạ i khi qua vị trí cân bằ ng (li độ bằ ng không, bằ ng không khi ở bi ên li đ ộ cự c đạ i.
b. Quãng đư ờ ng:
Neáu thì
4
Neáu thì 2
2
Neáu thì 4
T
t s A
T
t s A
t T s A
= =
= =
= =
suy ra
Neáu thì 4
Neáu thì 4
4
Neáu thì 4 2
2
tnT s n A
T
tnT s n A A
T
tnT s n A A
= =
= + = +
= + = +
Chú ý:
= = ↔ =±
= →
= − =± ↔ =±
= = ↔ =±
= →
= =± ↔ =±
2 2
neáu vaät ñi töø 0
2 2
82 2
1 neáu vaät ñi töø
2 2
3 3
neáu vaät ñi töø 0
2 2
6 neáu vaät ñi töø
2 2
M
m
M
m
s A x x A
T
t
s A x A x A
s A x x A
T
t
A A
s x x A
= = ↔ =±
= →
= − =± ↔ =±
neáu vaät ñi töø 0
2 2
3 3
12 1 neáu vaät ñi töø
2 2
M
m
A A
s x x
T
t
s A x A x A
2
T
4
T
12
T
6
T
8
T
8
T
6
T
12
T
2
A
3
2
A
2
2
A
-
A
A
O
a
c
m
/
s
2
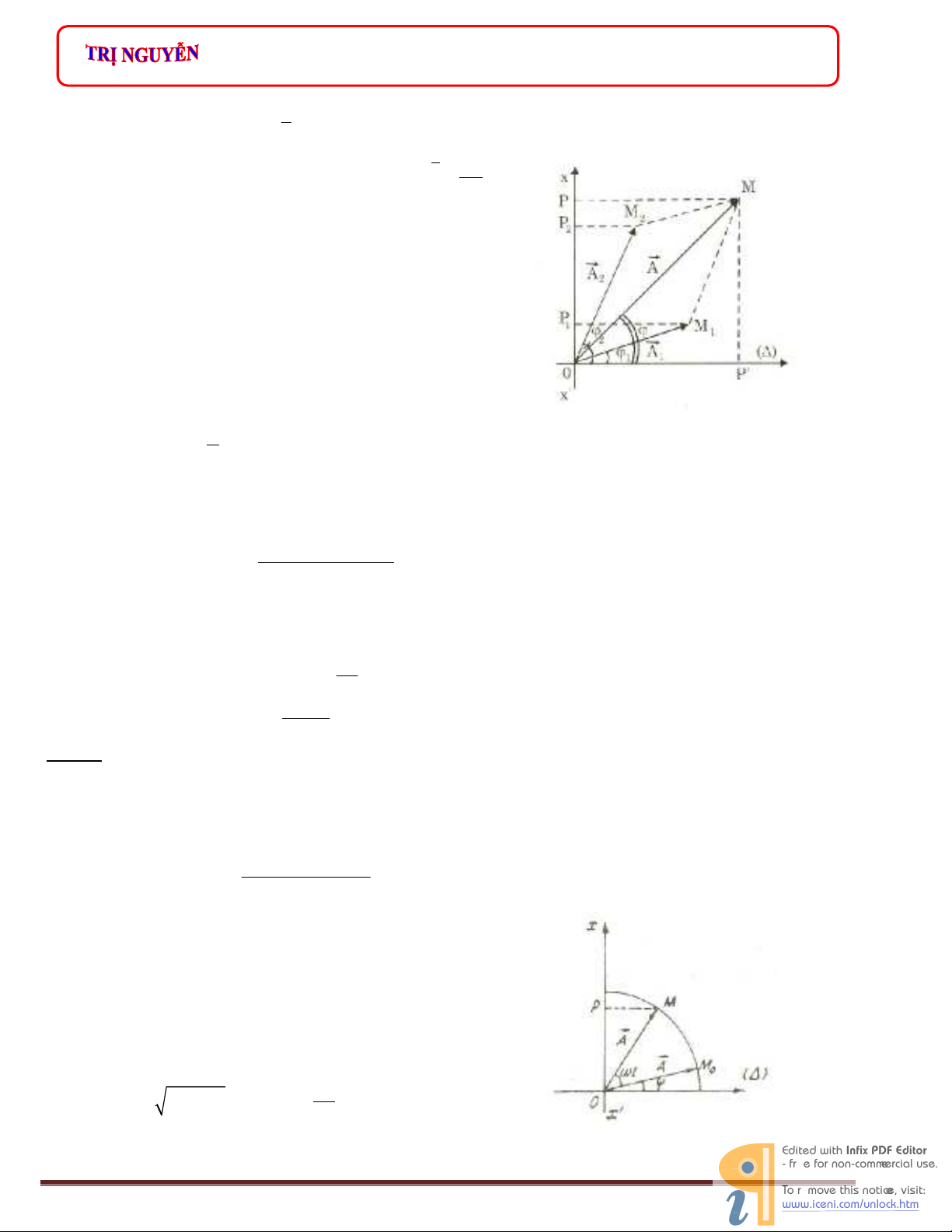
Sơ đồ phân bố thờ i gian trong quá trình dao độ ng
Trang 26
CHUYÊN ĐỀ VẬ T LÝ 12 LUYỆ N THI TN THPT –CAO ĐẲ NG –ĐẠ I HỌ C
c. + Tố c độ trung bình:
tb
s
vt
=
+ Tố c độ trung bình trong mộ t chu kỳ dao độ ng:
=4A
vT
14. Tổ ng hợ p dao dộ ng đề u hòa
a. Độ lệ ch pha trong hai dao độ ng cùng tầ n số
x
1
= A
1
cos
t +
1
và x
2
= A
2
cos
t +
2
-Độ lệ ch pha giữ a hai dao độ ng x
1
và x
2
:
1 2
∆ = −
+ Nế u
1 2
0
∆ > ⇔ >
thì x
1
nhanh pha hơ n x
2
+ Nế u
1 2
0
∆ < ⇔ <
thì x
1
chậ m pha hơ n x
2
-Các giá trị đặ t biệ t củ a độ lệ ch pha:
+
2k
∆=
vớ i
k Z∈
: hai dao độ ng cùng pha
+
2 1k
∆ = +
vớ i
k Z∈
: hai dao độ ng ngư ợ c pha
+
2 1 2
k
∆ = +
vớ i
k Z∈
: hai dao độ ng vuông pha
b. Tổ ng hợ p hai dao độ ng điề u hoà cùng phư ơ ng cùng tầ n số x
1
= A
1
cos
t +
1
và x
2
= A
2
cos
t +
2
đư ợ c mộ t dao độ ng điề u hoà cùng phư ơ ng, cùng tầ n số x = Acos
t +
.
Trong đó:
2 2 2
1 2 1 2 2 1
2osA A A A A c
= + + −
1 1 2 2
1 1 2 2
sin sin
tan os os
A A
A c A c
+
=+
vớ i ϕ
1
≤ϕ≤ϕ
2
nế u ϕ
1
≤ϕ
2
* Nế u ∆ϕ = 2kπ (x
1
, x
2
cùng pha ⇒A
Max
= A
1
+ A
2
`
* Nế u ∆ϕ = (2k + 1π (x
1
, x
2
ngư ợ c pha ⇒A
Min
=| A
1
-A
2
|
⇒| A
1
-A
2
|≤ A ≤ A
1
+ A
2
*Nế u A
1
= A
2
thì
1
1 2
A2A cos 2
2
∆ϕ
=
ϕ+ϕ
ϕ=
Chú ý : Khi viế t đư ợ c phư ơ ng trình dao độ ng x = Acos t + thì việ c xác đị nh vậ n tố c, gia tố c củ a vậ t như vớ i
m ộ t vậ t dao độ ng điề u hòa bình thư ờ ng.
c. Khi biế t mộ t dao độ ng thành phầ n x
1
= A
1
cos
t +
1
và dao đ ộ ng tổ ng hợ p x = Acos
t +
thì dao độ ng
thành phầ n còn lạ i là x
2
= A
2
cos
t +
2
.
Trong đó:
2 2 2
2 1 1 1
2osA A A AAc
= + − −
1 1
2
1 1
sin sin
tan os os
A A
Ac Ac
−
=−
vớ i ϕ
1
≤ϕ≤ϕ
2
n ế u ϕ
1
≤ϕ
2
d. Nế u mộ t vậ t tham gia đồ ng thờ i nhiề u dao độ ng điề u hòa
cùng phư ơ ng, cùng tầ n số có phư ơ ng trình x
1
= A
1
cos t +
1
;
x
2
= A
2
cos t +
2
;…thì dao độ ng tổ ng hợ p cũng là dao độ ng
điề u hoà cùng phư ơ ng cùng tầ n số x = Acos t + .
Chiế u lên trụ c Ox và trụ c Oy ⊥Ox .
Ta đư ợ c:
1 1 2 2
sin sin sin ...
y
A A A A
= = + +
2 2
x y
A A A⇒ = +
và
tan
x
y
A
A
=
vớ i
[ ]
min
;
Max
∈
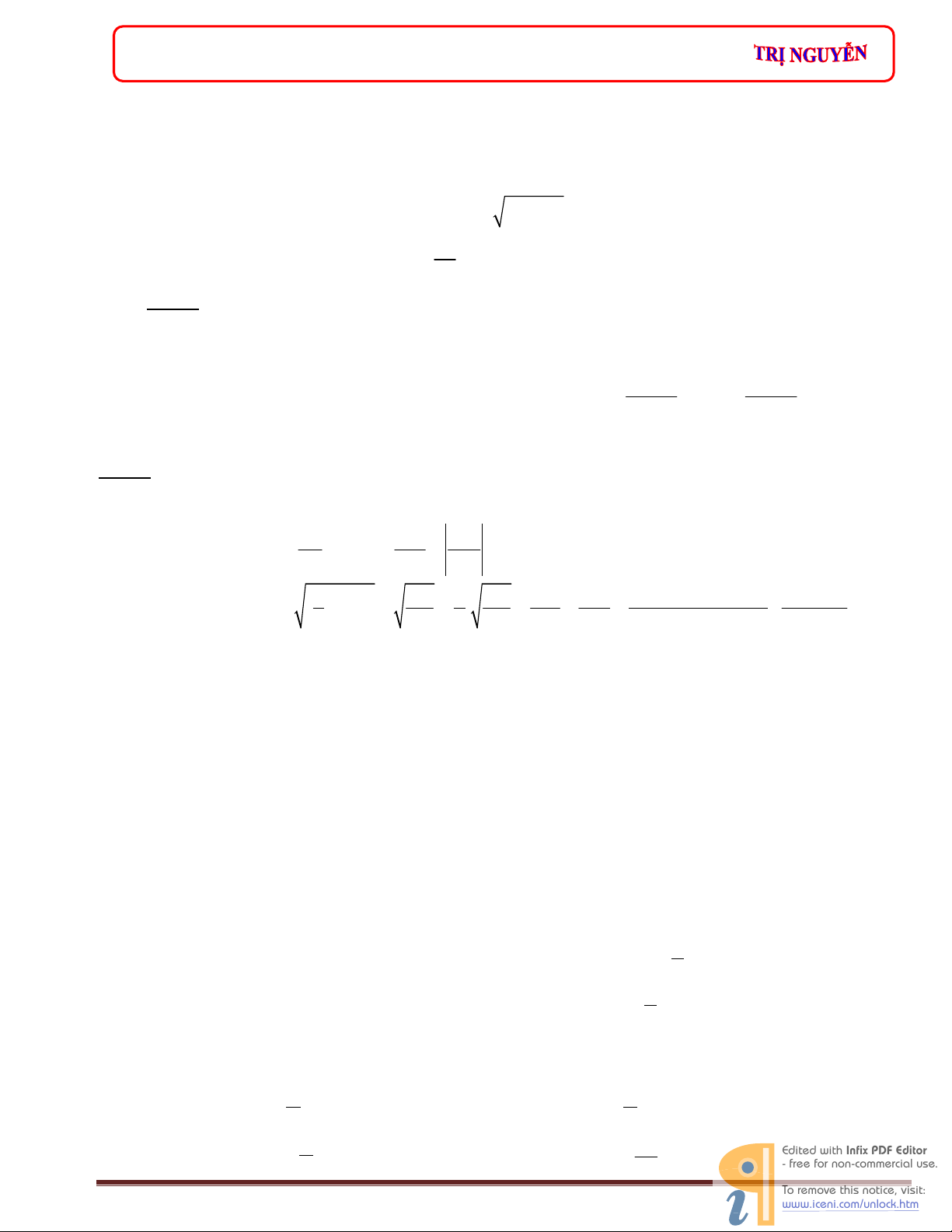
Trang 27
CHUYÊN ĐỀ VẬ T LÝ 12 LUYỆ N THI TN THPT –CAO ĐẲ NG –ĐẠ I HỌ C
e. Trư ờ ng hợ p tổ ng hợ p nhiề u dao độ ng điề u cùng phư ơ ng, cùng tầ n số : x
1
; x
2
; …; x
n
thì
x = x
1
+ x
2
+ … + x
n
=Acos
t +
-Tìm biên độ A: Chiế u xuố ng trụ c Ox :
1 1 2 2
cos cos ... cos
x n n
A A A A
= + + +
Chiế u xuố ng trụ c Oy :
1 1 2 2
sin sin ... sin
y n n
A A A A
= + + +
Biên độ tổ ng hợ p :
2 2
x y
A A A= +
-Pha ban đầ u củ a dao độ ng:
tan
x
y
A
A
= ⇒
Chú ý : + Tổ ng hợ p hai dao độ ng điề u hoà cùng phư ơ ng cùng tầ n số có thể áp dụ ng trư ờ ng hợ p tổ ng quát
nói trên.
+ Ngoài phư ơ ng pháp nói trên, nế u A
1
= A
2
= A, thì ta có thể cộ ng lư ợ ng giác và tìm đư ợ c
phư ơ ng trình dao độ ng tổ ng hợ p:
1 2 1 2
1 2 1 1 2 2
coscos2 cos cos 2 2
x x x A t A t A t
− +
= + = + + + = +
II. CÁC DẠ NG TOÁN VÀ PHƯ Ơ NG PHÁP GIẢ I
Dạ ng 1:Bài toán lậ p phư ơ ng trình dao độ ng dao độ ng điề u hoà:
* Viế t phư ơ ng trình dao độ ng tổ ng quát: x = Acos ωt + ϕ
* Xác đị nh A, ω,ϕ
+ Tính ω:
max max
max
22
= = = =
v a
f
T A v
+ Tính A :
2 2 m a x m a x m a x m i n
2
2 1 2
2 2
v a l l
v W W
A x k m
−
= + = = = = = =
chieàu daøi quyû ñaïo
+ Tính ϕdự a vào điề u kiệ n đầ u: lúc t = t
0
thư ờ ng t
0
= 0
0
0
A c o s
sin
x t
v A t
= +
⇒
=− +
Lư u ý: + Vậ t chuyể n độ ng theo chiề u dư ơ ng thì v > 0, ngư ợ c lạ i v < 0.
+ Trư ớ c khi tính ϕcầ n xác đị nh rõϕthuộ c góc phầ n tư thứ mấ y củ a đư ờ ng tròn lư ợ ng giác
thư ờ ng lấ y -π ≤ϕ≤π.
+ Khi 1 đạ i lư ợ ng biế n thiên theo thờ i gian ở thờ i điể m t
0
tăng thìđạ o hàm bậ c nhấ t củ a nó theo t
sẽ dư ơ ng và ngư ợ c lạ i.
MỘ T SỐ TRƯ Ờ NG HỢ P THƯ Ờ NG GẶ P ĐỐ I VỚ I BÀI TOÁN
LẬ P PHƯ Ơ NG TRÌNH DAO ĐỘ NG
Các k ế t quả dư ớ i đây chỉ mang tính chấ t tham khả o, họ c sinh không nên nhớkiể u máy móc
Nế u biể u diễ n x dư ớ i dạ ng cosin thì: Khi v > 0 ⇔-π<ϕ< 0
Khi v < 0 ⇔0 < ϕ≤π
Chọ n gố c thờ i gian
0
t0=
là
lúc vậ t qua vị trí cân bằ ng
0
x0=
theo chiề u dư ơ ng
0
v0>
: Pha ban đầ u
2
=−
lúc vậ t qua vị trí cân bằ ng
0
x0=
theo chiề u âm
0
v0<
: Pha ban đầ u
=2
lúc vậ t qua biên dư ơ ng
0
x A=
: Pha ban đầ u
0
=
lúc vậ t qua biên âm
0
x A=−
: Pha ban đầ u
=
lúc vậ t qua vị trí
0
2
A
x=
theo chiề u dư ơ ng
0
v0>
: Pha ban đầ u
3
=−
lúc vậ t qua vị trí
0
2
A
x=−
theo chiề u dư ơ ng
0
v0>
: Pha ban đầ u
=− 2
3