Së GD&§T Qu¶ng B×nh
§Ò kiÓm tra häc kú II - n¨m häc 2008-2009
Tr−êng
:
M«n: TOÁN ch.Tr×nh: Nâng cao líp: 12
Hä tªn
:
Thêi gian: 90 phót (kh«ng kÓ thêi gian giao ®Ò)
Sè
¸o danh:
§Ò cã
01
.
trang, gåm
cã
05
.
c©u.
Câu I (3.5 điểm).
Cho hàm số
2 1
1
x
y
x
+
=
−
.
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
2. Tìm tất cả các giá trị của tham số m để đường thẳng y=mx+1 cắt đồ thị của hàm
số đã cho tại hai điểm phân biệt.
C©u II. (2.0 ®iÓm)
1. Xét số phức z = x + yi . Tìm x, y sao cho
(
)
2
x yi 8 6i
+ = +
.
2. Gi¶i ph−¬ng tr×nh
.433
1
=+
−xx
C©u III. (1.0 ®iÓm)
Cho h×nh chãp S.ABC cã SA ⊥ (ABC), ∆ABC ®Òu c¹nh a, SA = a. TÝnh thÓ tÝch khèi
chãp S.ABC.
C©u IV (2.0 ®iÓm)
Trong hÖ täa ®é Oxyz, cho bốn ®iÓm A(0; 2; 4), B(4; 0; 4), C(4; 2; 0), D(4; 2; 4).
1. LËp ph−¬ng tr×nh mÆt cÇu ®i qua A, B, C, D.
2. TÝnh kho¶ng c¸ch tõ A tíi mÆt ph¼ng (BCD).
C©u V (1.5 ®iÓm). Cho h×nh ph¼ng giíi h¹n bëi c¸c ®−êng y=xe
x
; x=2 vµ y=0. TÝnh thÓ
tÝch cña vËt thÓ trßn xoay cã ®−îc khi h×nh ph¼ng ®ã quay quanh trôc Ox .
-HÕt-
Së gi¸o dôc vµ ®µo t¹o
QUẢNG BÌNH
ĐÁP ÁN SƠ LƯỢC
-
Thang ®iÓm
kiÓm tra häc kú II - n¨m häc 2008-2009
M«n: TOÁN ch.Tr×nh: Nâng cao líp: 12
(Gồm 3 trang )
Câu
Nội dung cần đạt được Điểm
CâuI
3,5
điểm
1. (2,0 điểm)
Tập xác định :
{
}
1\RD
=
0,25
S
ự
bi
ế
n thiên :
•
Chi
ề
u bi
ế
n thiên :
( )
2
3
y ' 0, x D.
x 1
−
= < ∀ ∈
−
Suy ra, hàm số nghịch biến trên mỗi khoảng
(
)
(
)
;1 1;
−∞ ∪ +∞
.
• Hàm số không có cực trị.
0,50
•
Gi
ớ
i h
ạ
n : →−∞ →+∞
= =
lim 2; lim 2
x x
y y
và
+ −
→ →
= +∞ = −∞
1 1
lim ; lim
x x
y y
.
Suy ra, đồ thị hàm số có một tiệm cận đứng là đường thẳng: x = 1,và
ti
ệm cận ngang l
à đư
ờng thẳng: y = 2.
0,50
•
B
ả
ng bi
ế
n thiên :
x
∞
−
1
∞
+
y
′
- -
y 2
∞
+
∞
−
2
0,25
•
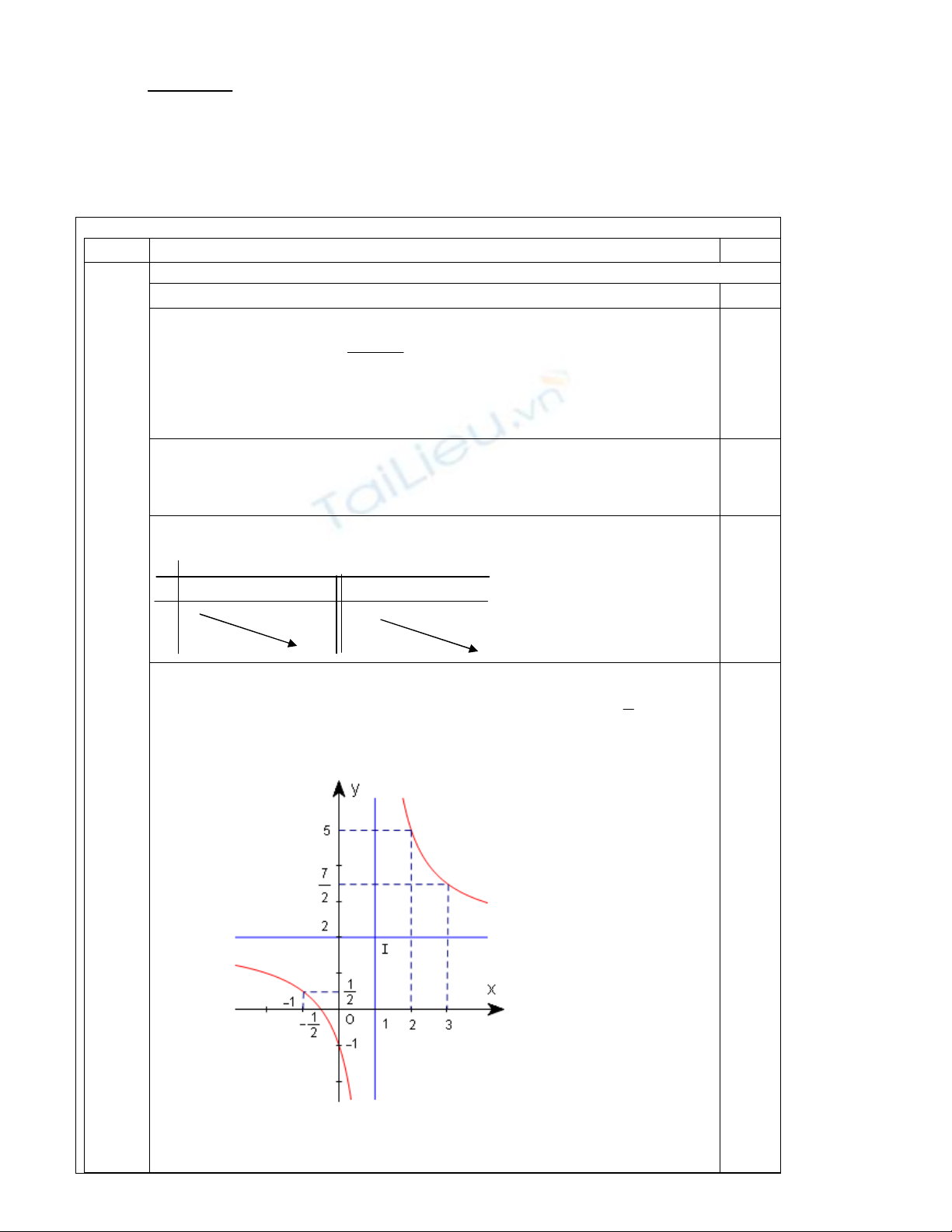
Đồ
th
ị
: (D
ạ
ng nh
ư
hình v
ẽ
)
-
Đồ
th
ị
c
ắ
t tr
ụ
c tung t
ạ
i
đ
i
ể
m (0;-1) và c
ắ
t tr
ụ
c hoành t
ạ
i
đ
i
ể
m 1
;0
2
−
.
- Đồ thị nhận điểm I (1;2) làm tâm đối xứng.
0,50
2. (1,5 điểm)
Đườ
ng th
ẳ
ng
y=mx+1 cắt đồ thị tại hai điểm phân biệt
⇔
Phương trình
(ẩn x)
2 1
1
1
x
mx
x
+
= +
− có hai nghi
ệ
m phân bi
ệ
t
⇔
Ph
ươ
ng trình (
ẩ
n x)
− + − =
2
mx (m 1)x 2 0
có hai nghi
ệ
m phân bi
ệ
t,
khác 1
0,75
≠
≠
⇔ ∆ = + + > ⇔
+ + >
− + − ≠
2
2
2
m 0
m 0
(m 1) 8m 0
m 10m 1 0
m.1 (m 1).1 2 0
< − −
⇔ − + < <
>
m 5 21
5 21 m 0
m 0
KL......
0,75
C©u II
2,0 ®iÓm
1.(1,0 điểm)
.Ta có:
(
)
2
yix +
= 8 + 6i
⇔
⇔
ixyiyx
682
22
+=+−
⇔
=
=−
3
8
22
xy
yx
⇔
{
}
1;3
=
=
yx
ho
ặ
c
{
}
1;3
−
=
−
=
yx
.
V
ậ
y giá tr
ị
x, y c
ầ
n tìm là
{
}
1;3
=
=
yx ho
ặ
c
{
}
1;3
−
=
−
=
yx
0.25
0.5
0.25
2. (1®iÓm) P.trình
⇔
4
3
3
3=+
x
x
§Æt t = 3
x
, t > 0. Ph−¬ng tr×nh trë thµnh
=
=
⇔=+−
3
1
034
2
t
t
tt
+) t = 1 ⇒ x = 0
+) t =3 ⇒ x = 1.
KL....
0,25®
0,25®
0,5®
C©u III
1 ®iÓm
ABCSABC
SSAV
∆
=.
3
1
Do ∆ABC ®Òu, c¹nh a nªn S
∆
ABC
=
4
3
2
a
Do ®ã ta ®−îc
12
3
3
.
a
V
ABCS
=
.
0,5®
0,5®
C©u IV
2 ®iÓm
1. (1 ®iÓm)
Gäi (S) lµ mÆt cÇu ®i qua A, B, C, D
Ph−¬ng tr×nh (S) cã d¹ng x
2
+ y
2
+ z
2
+ 2Ax + 2By + 2Cz + D = 0.( Điều kiện)
(S) ®i qua A, B, C, D ⇔
−=+++
−=++
−=++
−=++
36848
2048
3288
2084
DCBA
DBA
DCA
DCB
Gi¶i hÖ ®−îc A = -2, B = - 1, C = - 2, D = 0.
Thö l¹i vµ kÕt luËn ph−¬ng tr×nh mÆt cÇu (S) lµ
x
2
+ y
2
+ z
2
- 4x -2y - 4z = 0.
0,5®
0,25
0,25®
2. (1 ®iÓm)
)0;2;0(),4;2;0( =−= BDBC
.
MÆt ph¼ng (BCD) ®i qua B vµ cã vtpt lµ
)0;0;8(],[ =BDBC
Ph−¬ng tr×nh mÆt ph¼ng (BCD): x - 4 = 0.
Kho¶ng c¸ch tõ A tíi (BCD) lµ d = 4.
0,25®
0,25®
0,5®
C©u V
1,5 ®iÓm
LËp ®−îc c«ng thøc thÓ tÝch cÇn t×m V=
2
2 2
0
x
x e dx
π
∫
TÝnh ®óng V=
4
(5 1)
4
e
π
−
(§VTT).
0,5®
1,0®
Chú ý :- Giám khảo có thể chia nhỏ điểm thành phần để chấm.Điểm thành phần nhỏ nhất 0,25đ.
- Học sinh có thể làm cách khác với đáp án mà đúng vẫn cho điểm tối đa.
Hết