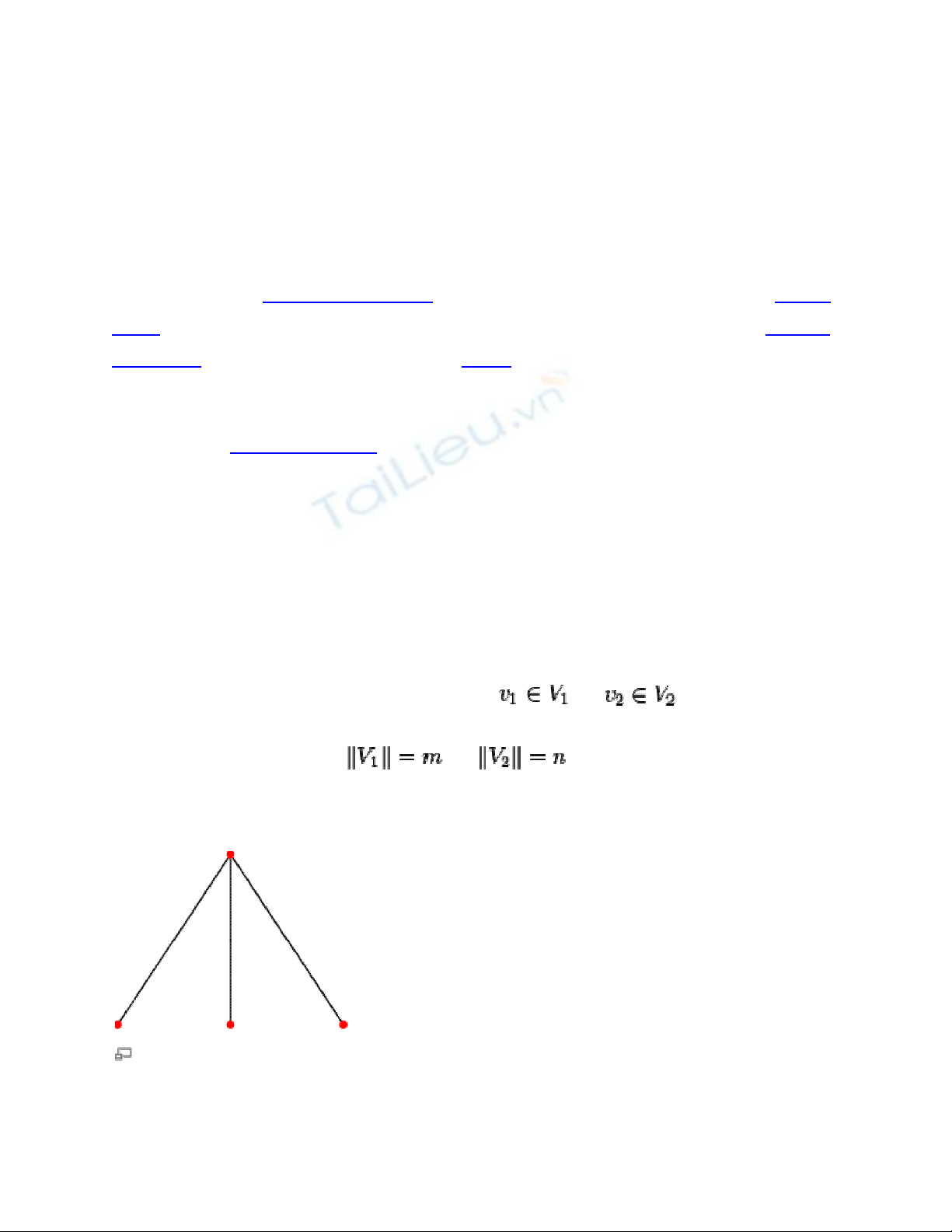
Đồ thị hai phía đầy đủ
Trong ngành lý thuyết đồ thị, một đồ thị hai phía đầy đủ (tiếng
Anh: complete bipartite graph hoặc biclique) là một dạng đồ thị
hai phía đặc biệt, trong đó mỗi đỉnh của tập thứ nhất nối với mọi
đỉnh thuộc tập thứ hai.
Cũng như đồ thị đầy đủ, đồ thị hai phía đầy đủ có các tính chất
rất thú vị.
định nghĩa
Một đồ thị hai phía đầy đủ G: = (V1 + V2,E) là một đồ thị hai
phía sao cho với mọi cặp hai đỉnh và , v1v2 là một
cạnh của đồ thị G. Một đồ thị hai phía hoàn hảo với các phân
hoạch có kích thước và được ký hiệu Km,n.
Ví dụ
K3,1
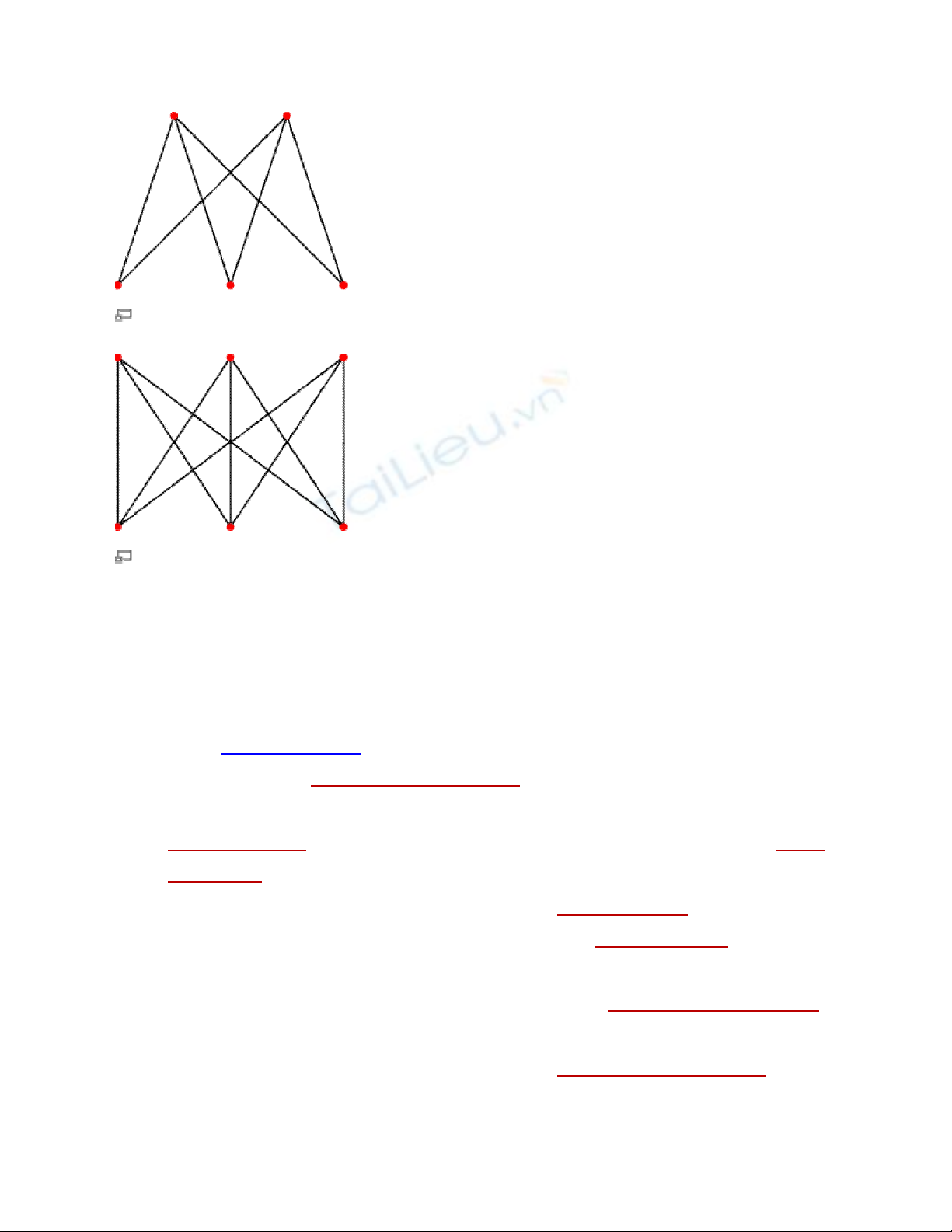
K3,2
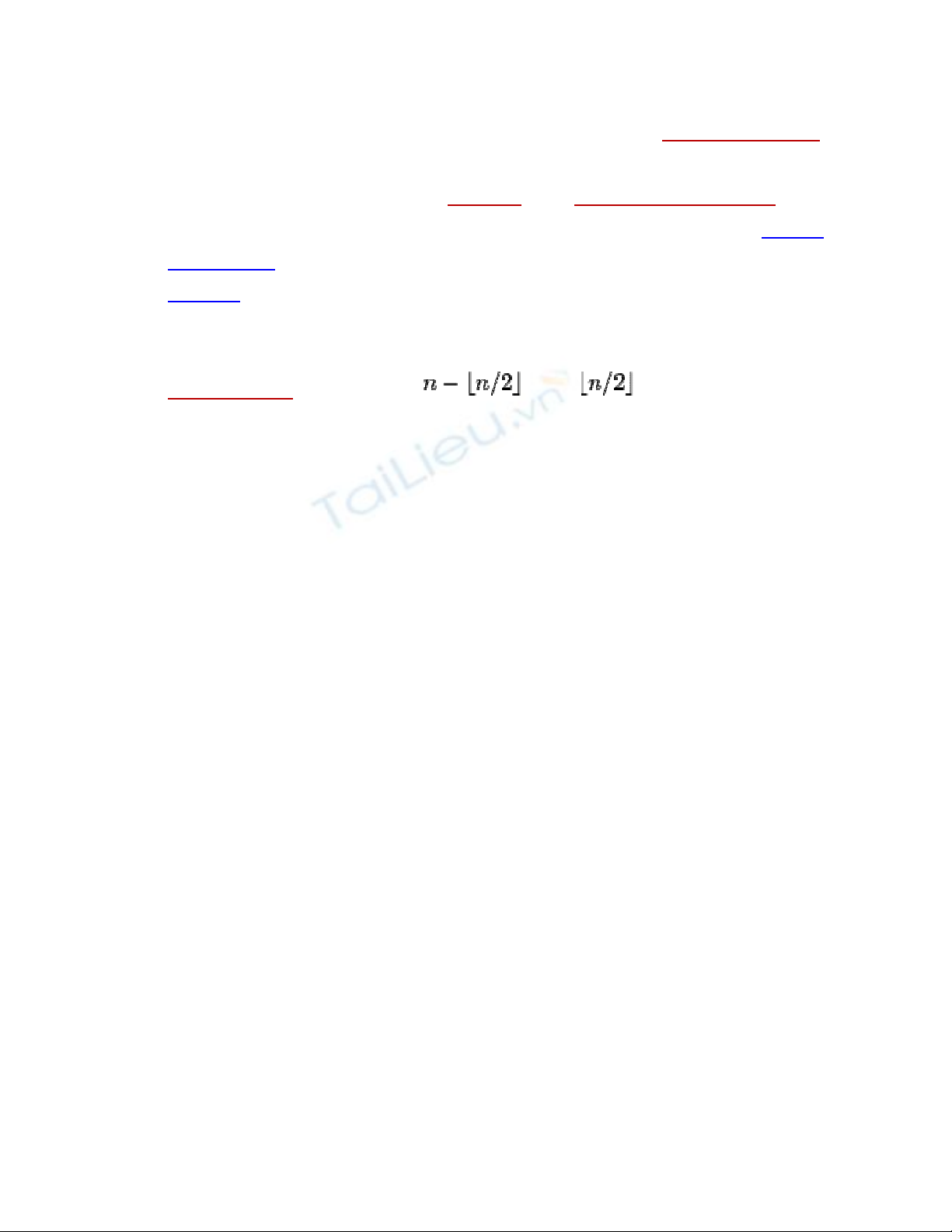
K3,3
Tính chất
Một đồ thị phẳng không thể có đồ thị con đồng phôi với đồ
thị K3,3; một đồ thị phẳng ngoài (outerplanar graph) không
thể chứa K2,3 dưới dạng một minor. (Đây không phải các
điều kiện đủ cho tính phẳng và phẳng ngoài, nhưng là điều
kiện cần.)
Một đồ thị hai phía đầy đủ Km,n có số phủ đỉnh (vertex
covering number) bằng min {m,n} và số phủ cạnh bằng
max {m,n}
Một đồ thị hai phía đầy đủ Km,n có một tập độc lập cực đại
(maximum independent set) có kích thước max{m,n}
Một đồ thị hai phía đầy đủ Km,n có cặp ghép hoàn hảo
(perfect matching) kích thước min{m,n}
Một đồ thị hai phía đầy đủ Kn,n có một cách tô màu n cạnh
đúng đắn
Hai kết quả cuối cùng là hệ quả của Định lý Hôn nhân
(Marriage Theorem) khi áp dụng cho đồ thị hai phía chính
quy bậc k.
Sắc số của đồ thị Km,n là 2.
Số màu cần thiết để tô màu các cạnh của Km,n là max{m.n}
để không có 2 cạnh nào cùng màu mà lại có chung đỉnh.
Chiều rộng của K1,n là , với là số tự nhiên nhỏ
nhất không vượt quá n/2