Đại Học Sư Phạm Tp. Hồ Chí Minh
Khoa Toán – Tin HọcLẬP TRÌNH WINDOWS
Thư viện đồ họa GDI
(Graphics Device Interface)
Trần Ngọc Bảo
Email: tnbao.dhsp@gmail.com
Lập trình đồ họa với thư viện GDI
Tran Ngoc Bao 2 Dai hoc Su Pham TP.HCM
TÌM HIỂUỨNG DỤNG PAINT
Chọn đối tượng
Di chuyển đối tượng
Lưu trữ các đối tượng
Vẽ các đối tượng trong GDI
Line
Rectangle
Circle
…
Tran Ngoc Bao 3 Dai hoc Su Pham TP.HCM
TÌM HIỂUỨNG DỤNG PAINT
Chọn đối tượng
Di chuyển đối tượng
Lưu trữ các đối tượng
Vẽ các đối tượng trong GDI
Line
Rectangle
Circle
Tran Ngoc Bao 4 Dai hoc Su Pham TP.HCM
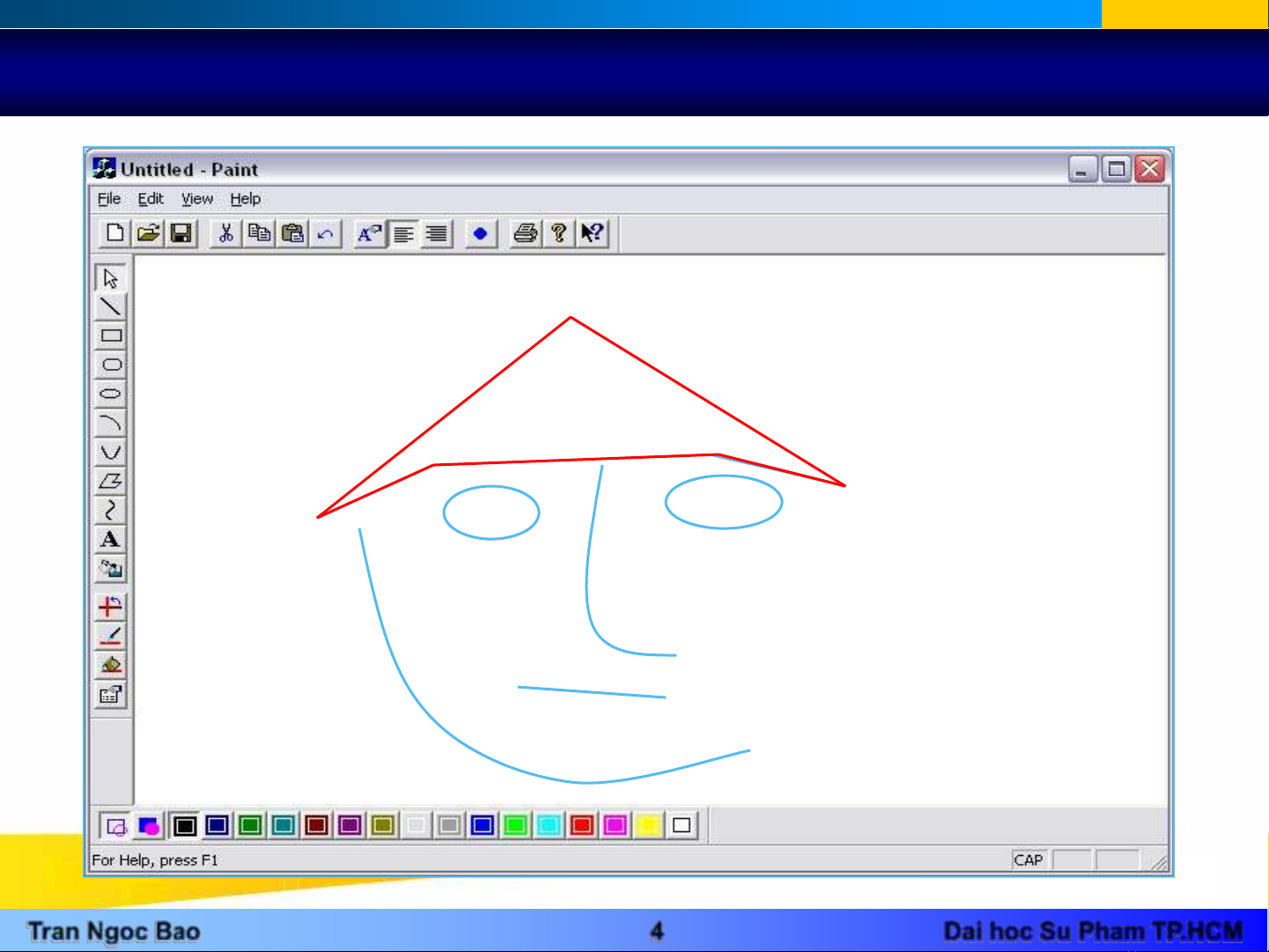
VẼ ĐỐI TƯỢNG
Demo chuong trinh Paint
Tran Ngoc Bao 5 Dai hoc Su Pham TP.HCM
TÌM HIỂUỨNG DỤNG PAINT
Chọn đối tượng
Di chuyển đối tượng
Lưu trữ các đối tượng
Vẽ các đối tượng trong GDI
Line
Rectangle
Circle