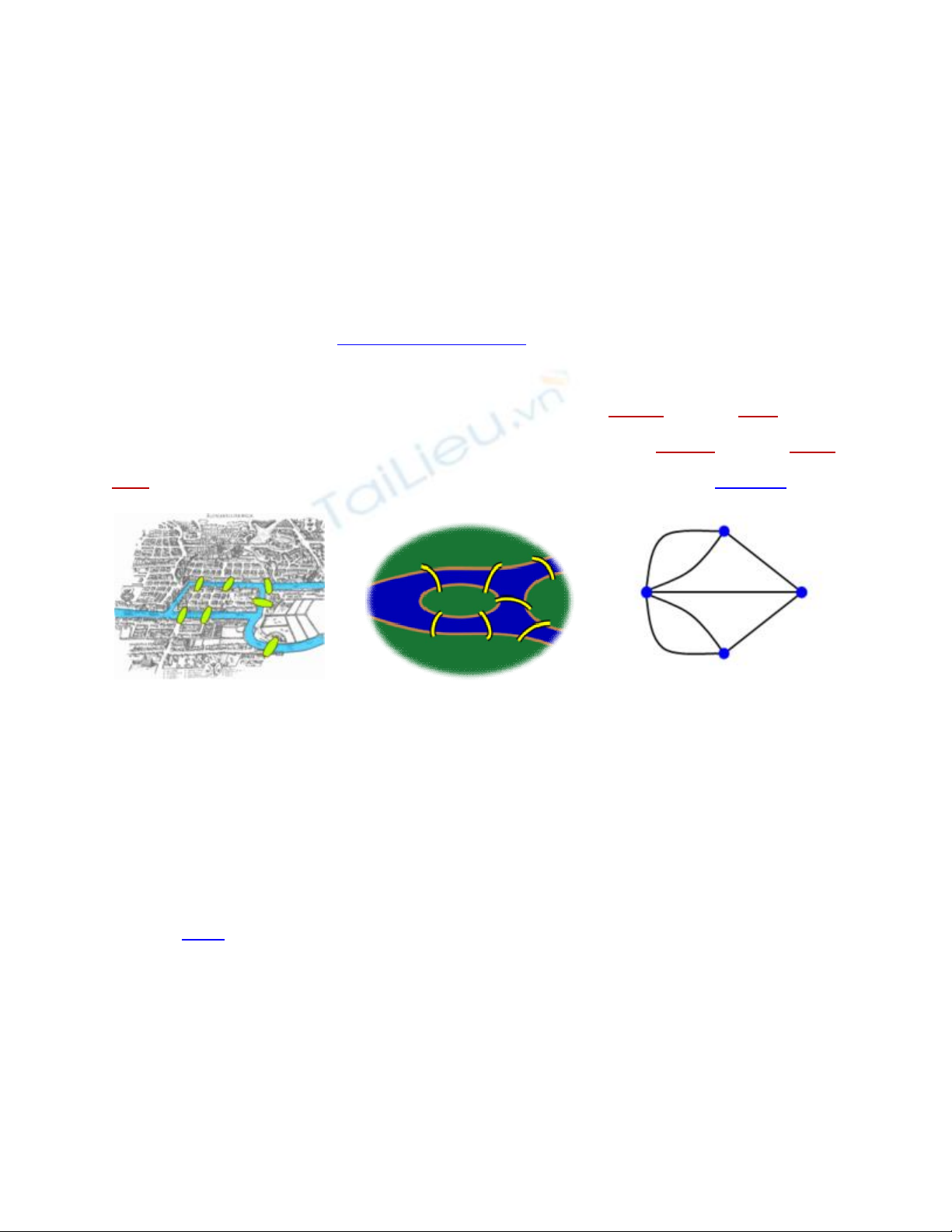
Lời giải của Euler
Để chứng minh kết quả, Euler đã phát biểu bài toán bằng
các thuật ngữ của lý thuyết đồ thị. Ông loại bỏ tất cả các
chi tiết ngoại trừ các vùng đất và các cây cầu, sau đó thay
thế mỗi vùng đất bằng một điểm, gọi là đỉnh hoặc nút, và
thay mỗi cây cầu bằng một đoạn nối, gọi là cạnh hoặc liên
kết. Cấu trúc toán học thu được được gọi là một đồ thị.
→ →
Hình thù của đồ thị có thể bị bóp méo theo đủ kiểu nhưng
không làm đồ thị bị thay đổi, miễn là các liên kết giữa các
nút giữ nguyên. Việc một liên kết thẳng hay cong, một nút
ở bên phải hay bên trái một nút khác là không quan trọng.
Euler nhận ra rằng bài toán có thể được giải bằng cách sử
dụng bậc của các nút. Bậc của một nút là số cạnh nối với
nó; trong đồ thị các cây cầu Königsberg, ba nút có bậc
bằng 3 và một nút có bậc 5. Euler đã chứng minh rằng
một chu trình có dạng như mong muốn chỉ tồn tại khi và
chỉ khi không có nút bậc lẻ. Một đường đi như vậy được
gọi là một chu trình Euler. Do đồ thị các cây cầu
Königsberg có bốn nút bậc lẻ, nên nó không thể có chu
trình Euler.
Có thể sửa đổi bài toán để yêu cầu một đường đi qua tất
cả các cây cầu nhưng không cần có điểm đầu và điểm
cuối trùng nhau. Đường đi như vậy được gọi là một
đường đi Euler. Một đường đi như vậy tồn tại khi và chỉ
khi đồ thị có đúng hai đỉnh bậc lẻ. (Như vậy điều này
cũng không thể đối với bảy cây cầu ở Königsberg.)