1. Neural nhân t oạ
Neural nhân t oạ là m t đ n v tính toán có nhi u đ u vàoộ ơ ị ề ầ (yi) và m t đ u raộ ầ
(a), m i đ u vào đ n t m t ỗ ầ ế ừ ộ liên k tế. Đ c tr ng c a neural là m t hàm kíchặ ư ủ ộ
ho tạ (f) phi tuy n chuy n đ i t h p tuy n tính c a t t c các tín hi u đ u vàoế ể ổ ổ ợ ế ủ ấ ả ệ ầ
thành tín hi u đ u ra. Hàm kích ho t này đ m b o ệ ầ ạ ả ả tính ch t phi tuy n ấ ế cho
tính toán c a m ng neural.ủ ạ H s đi u ch nh bệ ố ề ỉ có tác d ng tăng lên ụho c gi mặ ả
đi đ u vào th c c a hàm kích ho t, tùyầ ự ủ ạ theo nó d ng hay âmươ .
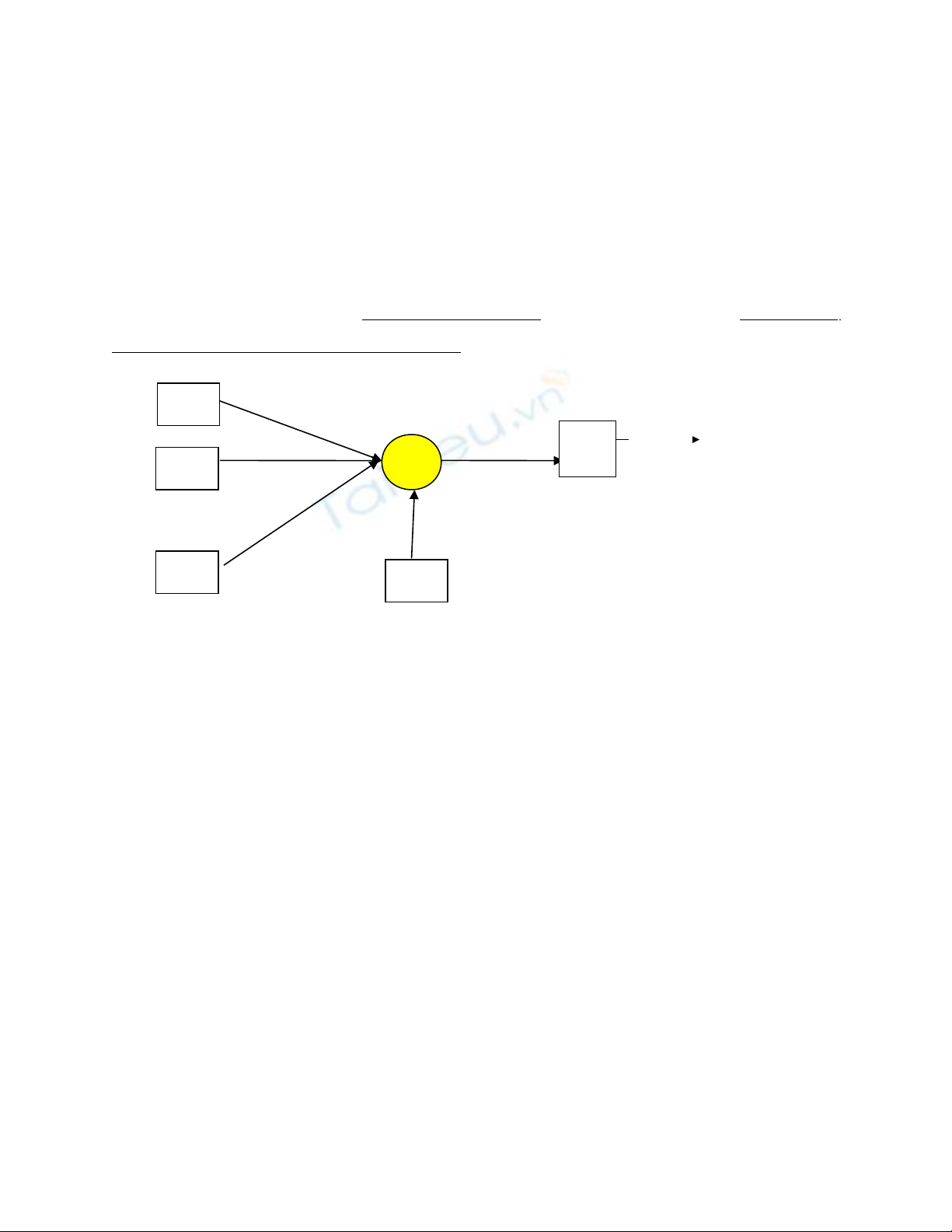
Hình1.1: Mô hình m t neural nhân t oộ ạ
M t neural đ c c u t o g m các thành ph n chính : ộ ượ ầ ạ ồ ầ
Liên k t neural.ế
B c ng . ộ ộ
Hàm kích ho t. ạ
w2
wk
w1
y1
y2
b0
yk
fa
Đ u vàoầĐ u ra a=f( ầ∑w’y+b)
2. M ng neural nhân t o.ạ ạ
Là m t h th ng bao g m nhi uộ ệ ố ồ ề ph n t x lý đ n gi n (hay còn g i làầ ử ử ơ ả ọ
neural) t a nh neural th n kinh c a não ng i, ho t đ ng song song và đ cự ư ầ ủ ườ ạ ộ ượ
n i v i nhau b i các liên k t neural. M i liên k t kèm theo m t tr ng s nào đó,ố ớ ở ế ỗ ế ộ ọ ố
đ c tr ng cho tính kích ho t ho c c ch gi a các neural. ặ ư ạ ặ ứ ế ữ
Mô hình m ng neural.ạ
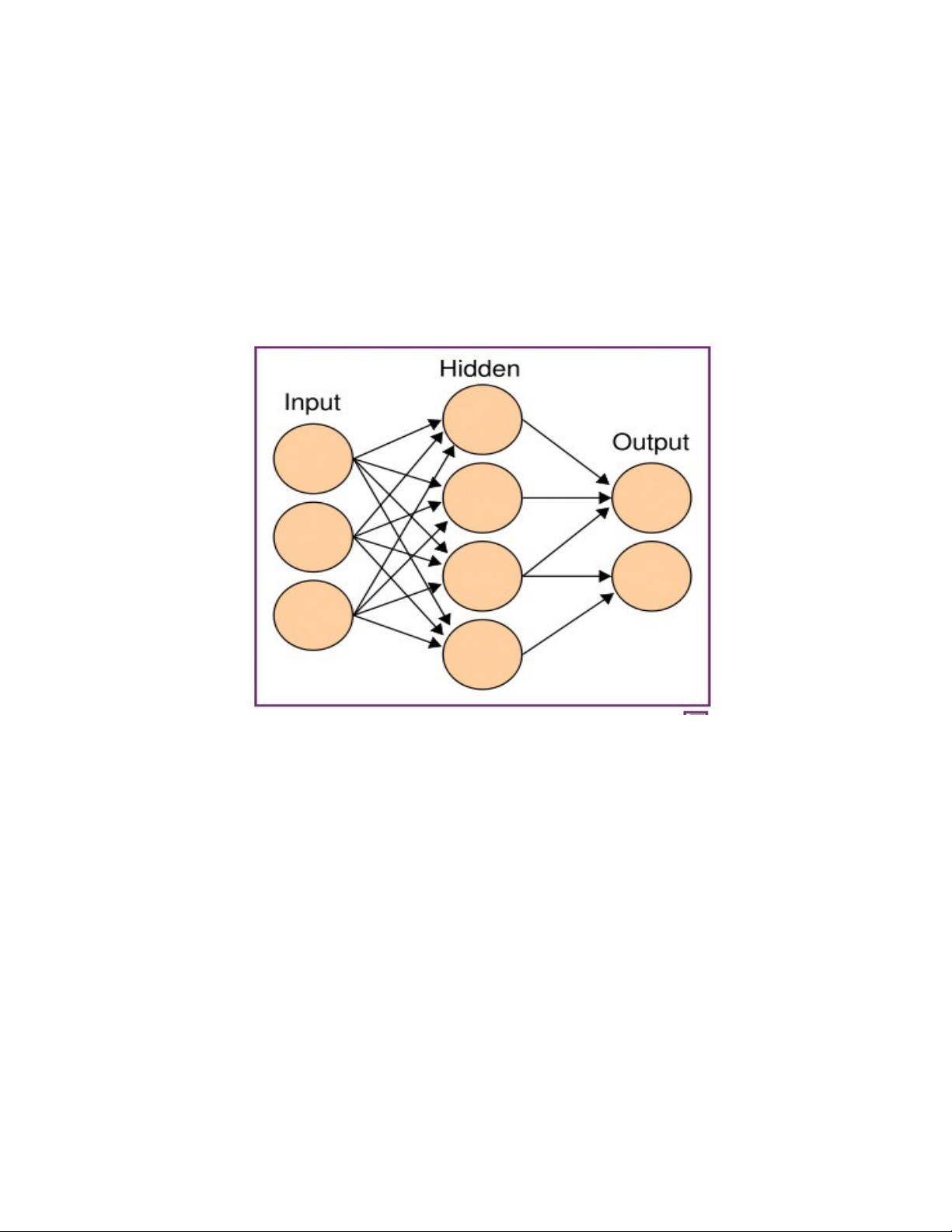
Hình 1.2: S đ đ n gi n v m t m ng neural nhân t oơ ồ ơ ả ề ộ ạ ạ
Mô hình m ng neural trên g m 3 l p: ạ ở ồ ớ
L p nh p (input).ớ ậ
L p n(hidden).ớ ẩ
L p xu t (output). ớ ấ
3. Thu t toán LAN TRUY N NG Cậ Ề ƯỢ
Xét m ng neural 3 l p : l p nh p, l p n và l p xu t.ạ ớ ớ ậ ớ ẩ ớ ấ
Hàm kích ho t các neural : logistic (sigmoid).ạ
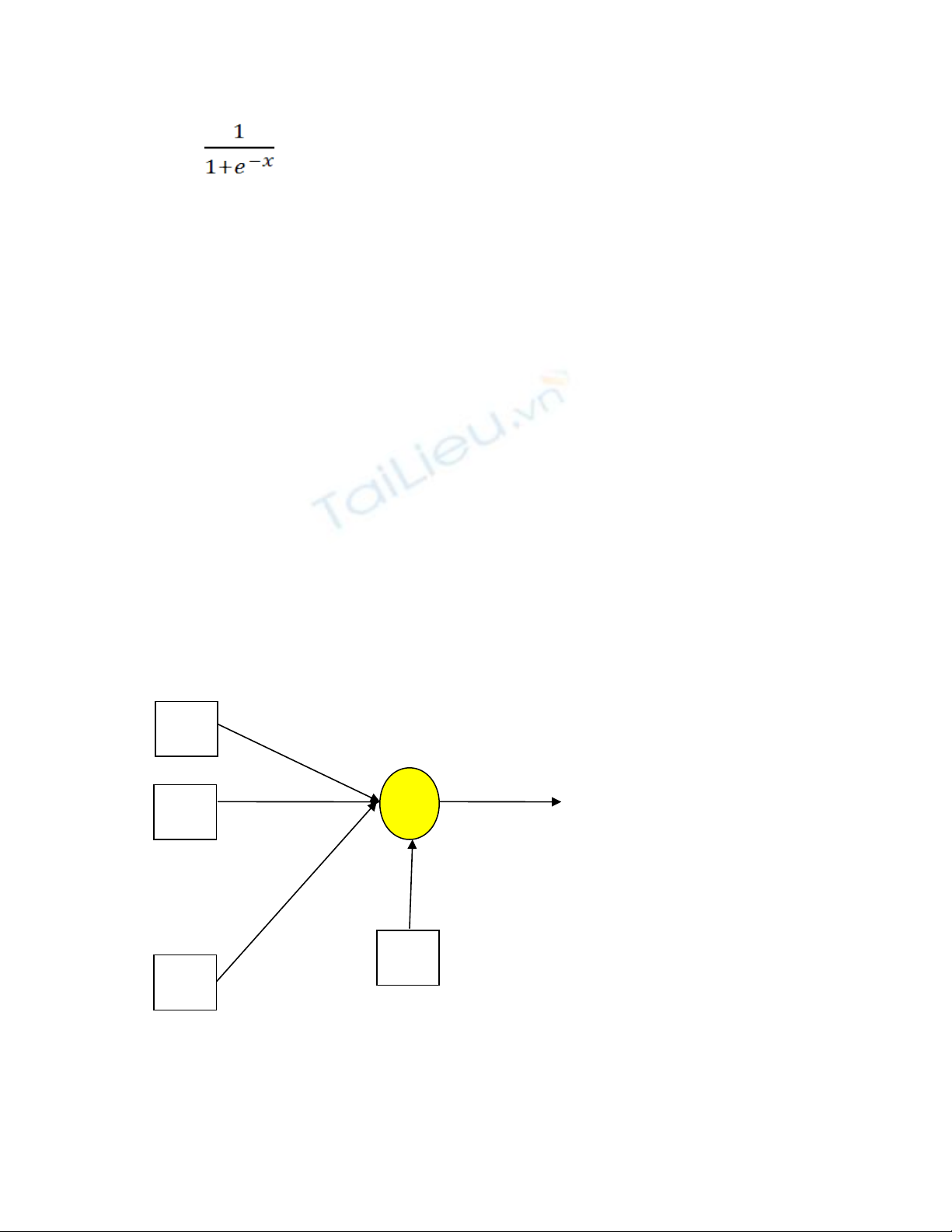
g(x)= (1.3)
B c 1: Kh i t o tr ng s w ng u nhiên nh .ướ ở ạ ọ ố ẫ ỏ
B c 2 : Ch n l p đ u vào x và đính nó vào l p đ u vào . ướ ọ ớ ầ ớ ầ
B c 3 : Truy n s kích ho t qua tr ng s đ n khi kich ho t các neuralướ ề ự ạ ọ ố ế ạ
đ u ra.ầ
B c 4: Tính đ o hàm riêng “ướ ạ δE” theo tr ng s cho l p xu t. s d ngọ ố ớ ấ ử ụ
GRADIENT c a hàm l i .ủ ỗ
B c 5: Tính đ o hàm riêng “ướ ạ δE” theo tr ng s cho l p n. s d ngọ ố ớ ẩ ử ụ
GRADIENT c a hàm l i. ủ ỗ
B c 6: C p nh t t t c tr ng s theo Wi=W(i-1)-µ(ướ ậ ậ ấ ả ọ ố δE/ δ Wi).
B c 7: quay lai “B c 2” cho đ n “B c 6” cho t t c các m u.ướ ướ ế ướ ấ ả ẫ
Trong đó: GRADIENT hàm l i:ỗ
Đ i v i các neural l p đ u ra:ố ớ ớ ầ
Hàm l i:ỗ
w2
wk
w1
z=g(v)
v=b0 +
g(x)=
y1
y2
b0
yk
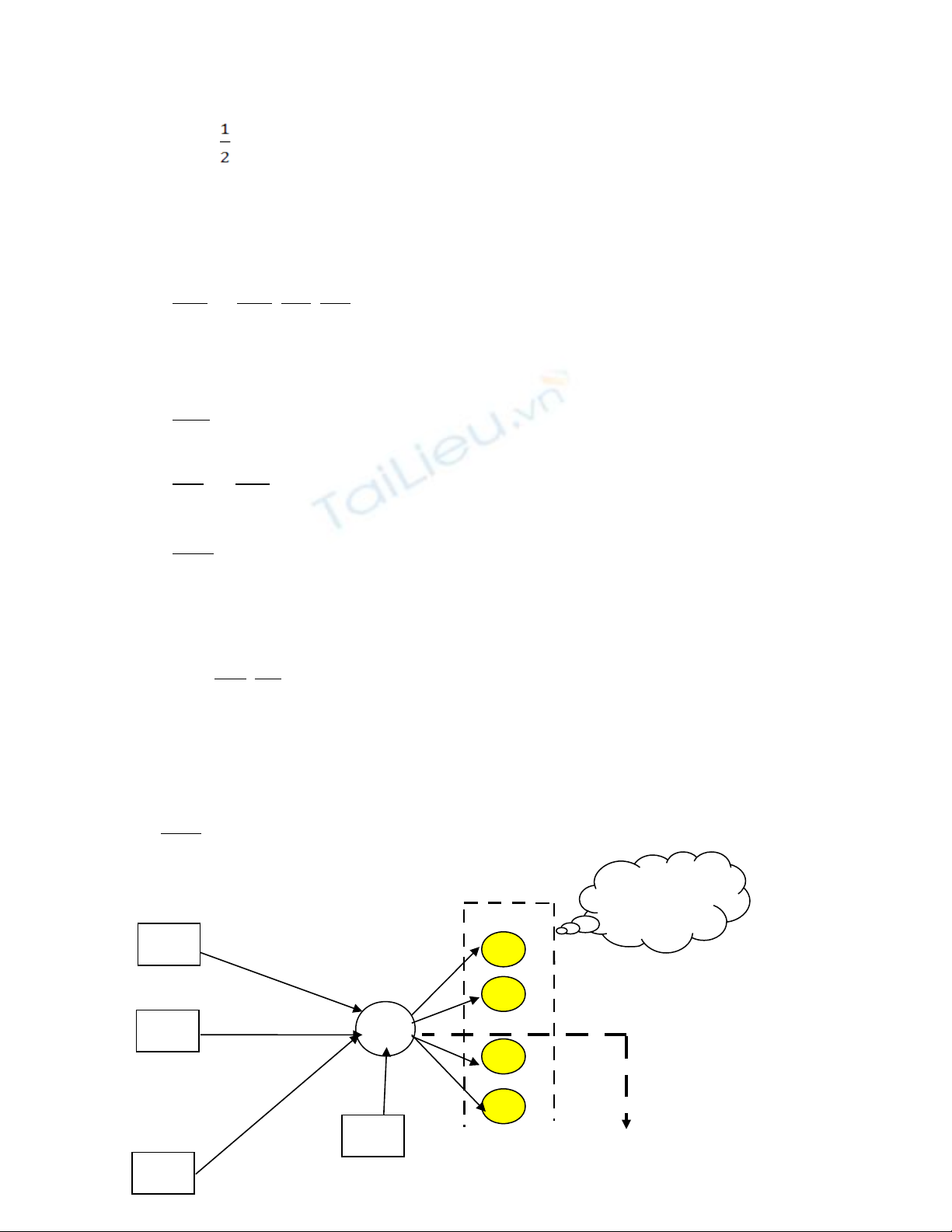
E(z)= (z - t)2
(1.4)
Đ o hàm riêng c a hàm l i theo tr ng s b:ạ ủ ỗ ọ ố
b
v
v
z
z
E
b
E
∂
∂
∂
∂
∂
∂
=
∂
∂
(1.5)
Ta có:
>
=
=
∂
∂
−=
∂
∂
=
∂
∂
−=
∂
∂
0,
0,1
)1(
)(
1
iy
i
b
v
zz
v
g
v
z
tz
z
E
i
Đ t:ặ
)1()(
−−=
∂
∂
∂
∂
=
zztz
v
z
z
E
p
Ta đ c:ượ
>
=
=
∂
∂
0
0
ipy
ip
b
E
i
i
(1.6)
Đ i v i các neural l p n:ố ớ ớ ẩ
a2
ad
a1
y=g(u)
v=a0 +
x1
x2
a0
L p đ u ớ ầ
ra
Đ o hàm riêng c a hàm l i theo tr ng s :ạ ủ ỗ ọ ố
a
u
u
y
y
E
a
E
∂
∂
∂
∂
∂
∂
=
∂
∂
(1.7)
Ta có:
( )
>
=
=
∂
∂
−=
∂
∂
=
∂
∂
=−−=
∂
∂
∂
∂∂
∂
∂
∂
∂
∂
=
∂
∂∑
=
0,
0,1
1
)1()(
1
jc
j
a
u
yy
u
y
b
y
v
pzztz
v
z
z
E
y
v
v
z
z
E
y
E
j
j
i
i
iiiii
i
i
i
K
i
i
i
i
i
Đ t:ặ
)1(
1
yybp
u
y
y
E
q
K
i
ii
−
=
∂
∂
∂
∂
=
∑
=