•Slide bài gi ng này đ c thi t k nh m ả ượ ế ế ằ
giúp h c sinh h th ng l i nh ng n i dung ọ ệ ố ạ ữ ộ
c b n có trong đ thi Toán l p 9, đ thi ơ ả ề ớ ề
Toán kỳ thi t t nghi p THCS.ố ệ
•Phù h p cho h c sinh Trung bình và Khá ợ ọ
có th h th ng và n m v ng nh ng n i ể ệ ố ắ ữ ữ ộ
dung c b n trong đ thi đ có th ôn t p ơ ả ề ể ể ậ
hi u qu nh m đ t đi m cao trong kì thi ệ ả ằ ạ ể
l p 9 lên l p 10.ớ ớ
Ng i so n: Miss Hi n. ườ ạ ề
SĐT:0128.396.4956 1
Ôn thi Toán l p 9ớ
1.Gi i ph ng trình b c , gi i h ph ng trìnhả ươ ậ ả ệ ươ
2.Bài toán rút g n.ọ
3.Gi i toán b ng cách l p h ph ng trình, ả ằ ậ ệ ươ
ph ng trình.ươ
4.V đ th c a đ ng th ng, parapol, tìm giao ẽ ồ ị ủ ườ ẳ
đi m c a đ ng th ng và parapol.ể ủ ườ ẳ
5.Tìm đi u ki n c a m đ ph ng trình b c 2 ề ệ ủ ể ươ ậ
có nghi m th a yêu c u bài toán.ệ ỏ ầ
2
Ng i so n: Miss Hi n. ườ ạ ề
SĐT:0128.396.4956
Ph n 1: Gi i ph ng trình b c 2 và ầ ả ươ ậ
h ph ng trìnhệ ươ
•Ph ng trình (pt) b c 2 có d ng t ng quát ươ ậ ạ ổ
là:
•B c 1 : ta coi pt đã có d ng t ng quát ướ ạ ổ
hay ch a n u ch a thì ta đ a pt v đúng ư ế ư ư ề
d ng t ng quát nh trên. Sau đó xác đ nh ạ ổ ư ị
các h s a, b, c.ệ ố
•B c 2: Tính ướ
2
ax 0bx c
+ + =
2
4b ac
∆ = −
3
Ng i so n: Miss Hi n. ườ ạ ề
SĐT:0128.396.4956
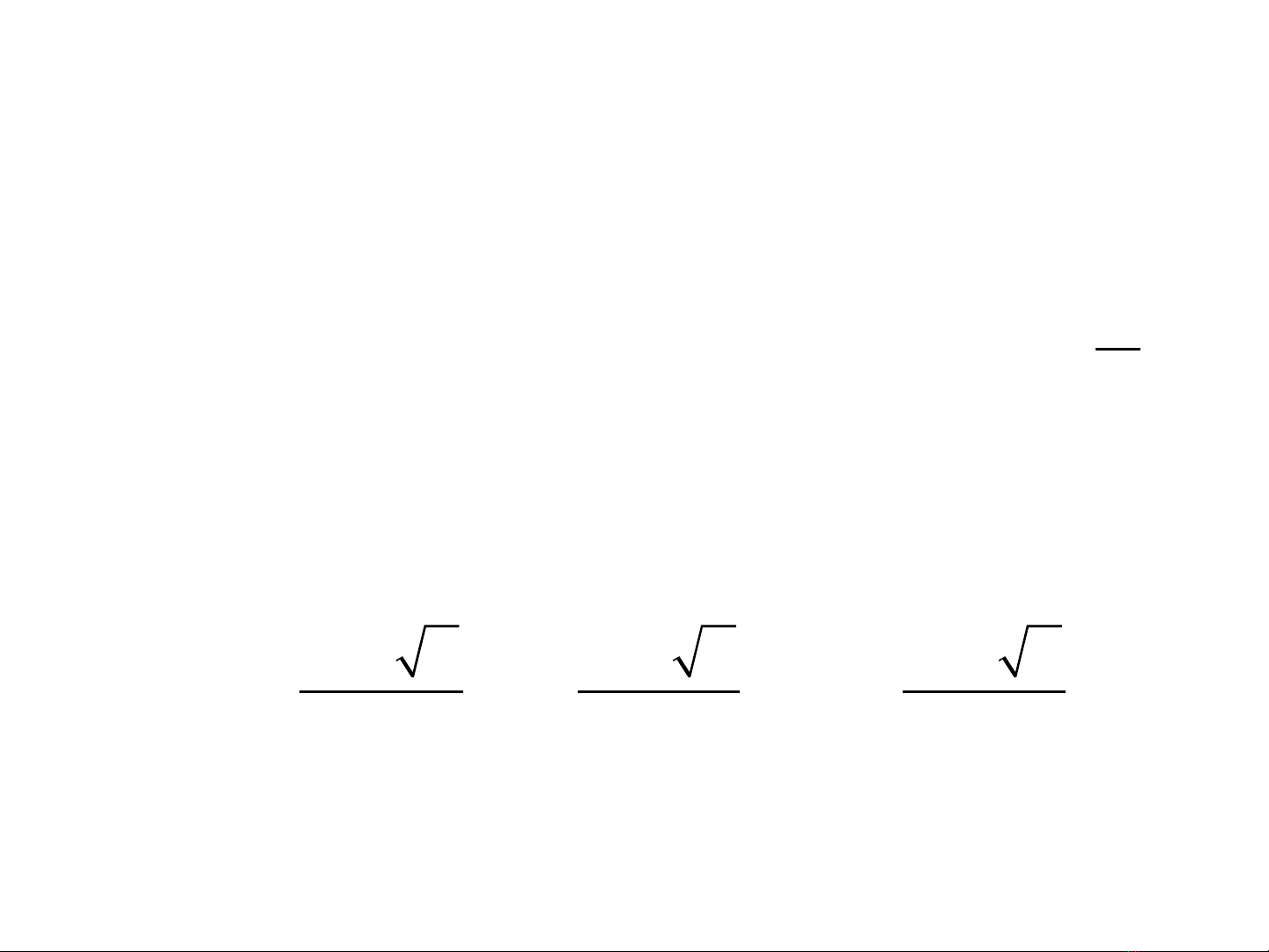
•B c 3: Xét xem ∆<0 hay ∆=0 hay ∆>0.ướ
N u ∆<0: ta k t lu n pt vô nghi mế ế ậ ệ
N u ∆=0: ta k t lu n pt có nghi m képế ế ậ ệ
N u ∆>0: ta k t lu n pt có 2 nghi m phân ế ế ậ ệ
bi t ệ
2
b
xa
−
=
1 2
; ( )
2 2 2
b b b
x x hayx
a a a
− + ∆ − − ∆ − ∆
= = =
4
Ng i so n: Miss Hi n. ườ ạ ề
SĐT:0128.396.4956
Đi m quan tr ng khi gi i ph ng ể ọ ả ươ
trình b c 2ậ
Đ a ph ng trình b c 2 v đúng d ng t ng ư ươ ậ ề ạ ổ
quát.
Xác đ nh chính xác các h s a, b, c trong ị ệ ố
ph ng trình b c 2.ươ ậ
Chú ý: Trong bài gi ng này s không gi i ả ẽ ớ
thi u cách gi i pt b c hai b ng công th c ệ ả ậ ằ ứ
∆’ vì 2 lý do: công th c ∆’ ch áp d ng cho ứ ỉ ụ
tr ng h p h s b ch n và n u ph i nh ườ ợ ệ ố ẵ ế ả ớ
cùng lúc 2 công th c ∆ và công th c ∆’ thì ứ ứ
d b nh m l n.ễ ị ầ ẫ 5
Ng i so n: Miss Hi n. ườ ạ ề
SĐT:0128.396.4956