
1. L i gi i thi u: ờ ớ ệ
Ch đ hàm s là m t n i dung c b n c a ch ng trình toán THPT. M tủ ề ố ộ ộ ơ ả ủ ươ ộ
bài toán v ch đ hàm s không ch đn thu n là tìm t p xác đnh, xét s bi nề ủ ề ố ỉ ơ ầ ậ ị ự ế
thiên và v đ th c a hàm s mà còn đ c p đn nh ng v n đ khác nh : tìm giáẽ ồ ị ủ ố ề ậ ế ữ ấ ề ư
tr l n nh t, giá tr nh nh t c a hàm s trên m t kho ng, đo n. ng d ng cách tìmị ớ ấ ị ỏ ấ ủ ố ộ ả ạ Ứ ụ
giá tr l n nh t, giá tr nh nh t c a hàm s vào gi i quy t các bài toán th c t ,ị ớ ấ ị ỏ ấ ủ ố ả ế ự ế
gi m chi phí, nâng cao ch t l ng và hi u qu trong công vi c…ả ấ ượ ệ ả ệ
N i dung tìm giá tr l n nh t, giá tr nh nh t c a hàm s là m t trong nh ngộ ị ớ ấ ị ỏ ấ ủ ố ộ ữ
n i dung quan tr ng và th ng g p trong các k thi THPT Qu c gia trong nh ngộ ọ ườ ặ ỳ ố ữ
năm g n đây, nh ng r t nhi u h c sinh còn m h và lúng túng không bi t gi i bàiầ ư ấ ề ọ ơ ồ ế ả
toán này. Bài toán tìm giá tr l n nh t, giá tr nh nh t c a hàm s có nhi u d ngị ớ ấ ị ỏ ấ ủ ố ề ạ
khác nhau. H c sinh không bi t phân lo i bài t p đ có cách gi i h u hi u, trongọ ế ạ ậ ể ả ữ ệ
quá trình làm bài t p r t nhi u bài gi i h c sinh còn b sót tr ng h p.ậ ấ ề ả ọ ỏ ườ ợ
H c sinh m i ch đc ti p c n và hi u bi t bài toán tìm giá tr l n nh t, giáọ ớ ỉ ượ ế ậ ể ế ị ớ ấ
tr nh nh t c a hàm s m c đ nh t đnh; ch a hi u sâu v lí thuy t; ch a đcị ỏ ấ ủ ố ở ứ ộ ấ ị ư ể ề ế ư ượ
rèn luy n nhi u v kĩ năng. Chính vì v y tôi m nh d n vi t sáng ki n kinh nghi mệ ề ề ậ ạ ạ ế ế ệ
v bài toán tìm giá tr l n nh t, giá tr nh nh t c a hàm s v i mong mu n giúpề ị ớ ấ ị ỏ ấ ủ ố ớ ố
h c sinh hi u sâu h n v bài toán này và đc rèn kĩ năng nhi u h n, v n d ng vàoọ ể ơ ề ượ ề ơ ậ ụ
gi i toán thành th o h n, đó là lí do tôi ch n đ tài sáng ki n kinh nghi m: “ ngả ạ ơ ọ ề ế ệ Ứ
d ng đo hàm đ tìm giá tr l n nh t và giá tr nh nh t c a hàm s ”ụ ạ ể ị ớ ấ ị ỏ ấ ủ ố
2. Tên sáng ki n:ế “ ng d ng đo hàm đ tìm giá tr l n nh t và giá tr nhỨ ụ ạ ể ị ớ ấ ị ỏ
nh t c a hàm s ”ấ ủ ố
3. Tác gi sáng ki n:ả ế
- H và tên: NGUY N TH TH Mọ Ễ Ị Ơ
- Đa ch : Tr ng THPT Tr n H ng Đo- Tam D ng –Vĩnh Phúc.ị ỉ ườ ầ ư ạ ươ
- S đi n tho i: 0985794595 ố ệ ạ
- Email: nguyenthithom.gvtranhungdao@vinhphuc.edu.vn
4. Ch đu t t o ra sáng ki n: ủ ầ ư ạ ế Nguy n Th Th mễ ị ơ
1

5. Lĩnh v c áp d ng sáng ki n: ự ụ ế Áp d ng vào bài 3: ụGiá tr l n nh t và giá trị ớ ấ ị
nh nh t c a hàm sỏ ấ ủ ố – Ch ng I: ng d ng c a đo hàm đ kh o sát và v đươ Ứ ụ ủ ạ ể ả ẽ ồ
th c a hàm s . Trong ch ng trình Gi i tích 12 b c THPT. C th nh sau:ị ủ ố ươ ả ậ ụ ể ư
- V phía h c sinh, tôi l a ch n h c sinh các l p 12A3, 12A4 tr ng THPTề ọ ự ọ ọ ớ ườ
Tr n H ng Đo – Tam D ng – Vĩnh Phúc, do tôi tr c ti p gi ng d y năm h cầ ư ạ ươ ự ế ả ạ ọ
2018– 2019.
6. Ngày sáng ki n đc áp d ng l n đuế ượ ụ ầ ầ : Năm h c 2018 -2019.ọ
7. Mô t b n ch t c a sáng ki n:ả ả ấ ủ ế
PH N I. N I DUNG C A SÁNG KI NẦ Ộ Ủ Ế
I. C S LÍ THUY TƠ Ở Ế
1. ĐNH NGHĨAỊ :
Cho HS xác đnh trên t p Dị ậ
a) S M g i là GTLN c a HS trên t p D n u và sao cho ố ọ ủ ậ ế
Kí hi u ệ
b) S ốm g i là giá tr l n nh t c a trên D n u sao cho ọ ị ớ ấ ủ ế
Kí hi u ệ
2. NH N XÉTẬ
Cho hàm s liên t c trên đo n ố ụ ạ
N u gi nguyên d u trên đo n thì đt giá tr l n nh t và giá tr nh nh t t iế ữ ấ ạ ạ ị ớ ấ ị ỏ ấ ạ
các đu mút c a đo n.ầ ủ ạ
3. QUY T C TÌM GIÁ TR L N NH T, GIÁ TR NH NH T C A HÀM SẮ Ị Ớ Ấ Ị Ỏ Ấ Ủ Ố
LIÊN T C TRÊN ĐO N Ụ Ạ
B c 1. Tìm các đi m trên kho ng mà t i đó ướ ể ả ạ ho c không xác đnhặ ị
B c 2. Tính ướ
.
B c 3. Tìm s l n nh t M và s nh nh t m trong các s trên. Ta cóướ ố ớ ấ ố ỏ ấ ố
4. CHÚ Ý KHI TÌM GIÁ TR L N NH T, GIÁ TR NH NH T:Ị Ớ Ấ Ị Ỏ Ấ
N u hàm s liên t c và đng bi n (ngh ch bi n) trên ế ố ụ ồ ế ị ế thì và (và ).
N u hàm s là hàm s tu n hoàn v i chu k thì đ tìm GTLN, GTNN c aế ố ố ầ ớ ỳ ể ủ
nó trên ta ch c n tìm GTLN, GTNN trên m t đo n có đ dài b ng .ỉ ầ ộ ạ ộ ằ
Khi bài toán yêu c u tìm GTLN, GTNN mà không nói trên t p nào thì taầ ậ
hi u là tìm GTLN, GTNN trên t p xác đnh c a hàm s .ể ậ ị ủ ố
2
PH N II. CÁC D NG TOÁNẦ Ạ
D NG 1. TÌM GIÁ TR L N NH T – GIÁ TR NH NH T C A HÀM SẠ Ị Ớ Ấ Ị Ỏ Ấ Ủ Ố
1.1. Tìm giá tr l n nh t – giá tr nh nh t c a hàm s trên kho ng ị ớ ấ ị ỏ ấ ủ ố ả
Ph ng phápươ
T lu nự ậ
Xét hàm s trên kho ng . Tính ố ả
Tìm các đi m , t i đó ho c không xác đnh.ể ạ ặ ị
L p b ng bi n thiên c a hàm s trên kho ng ậ ả ế ủ ố ả
K t lu nế ậ
Tr c nghi m:ắ ệ
Nh p MODE 7 . ậ.
Start? End? Step? .
Nhìn b ng giá tr . K t lu n.ả ị ế ậ
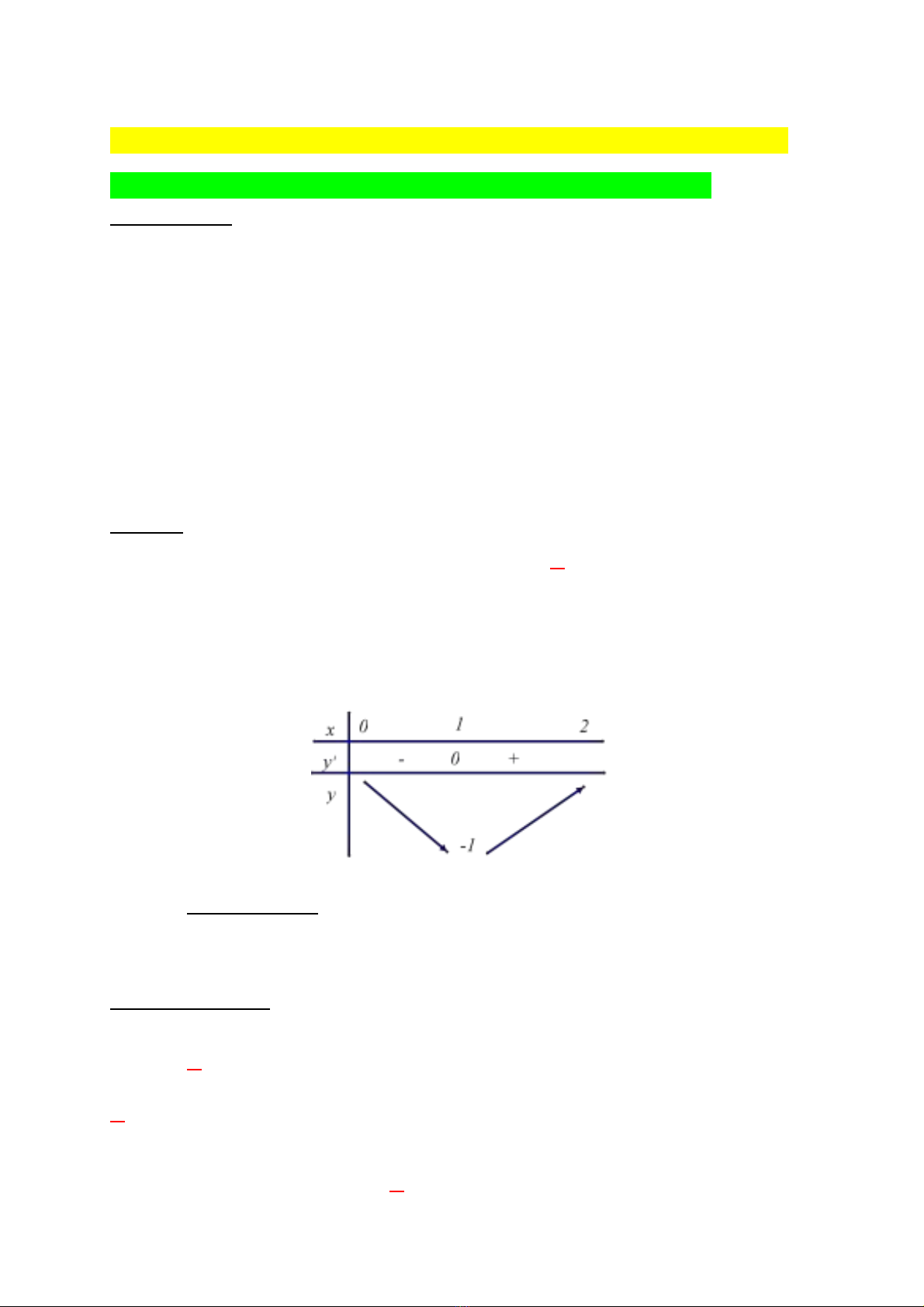
Ví d 1:ụ Giá tr nh nh t c a hàm s ị ỏ ấ ủ ố
3
3 1y x x
= − +
trên kho ng ả
( )
0;2
là
A.
3
.B.
1
.C.
−1
D.
0
L i gi iờ ả
TXĐ: R
L p BBT:ậ
T BBT suy ra, ừ
S d ng Casioử ụ
Nh p MODE 7 . ậ.
Start? End? Step? . K t lu n.ế ậ
Bài t p t ng t :ậ ươ ự
Câu 1. Giá tr nh nh t c a hàm s trên kho ng là:ị ỏ ấ ủ ố ả
A. B. C. D.
Câu 2. (MH – 2017) Tìm giá tr nh nh t c a hàm s trên kho ng ị ỏ ấ ủ ố ả
A. B. C. D.
Câu 3. Tìm giá tr nh nh t c a hàm s trên n a kho ng.ị ỏ ấ ủ ố ử ả
A. B. C. D.
3

Câu 4. G i giá tr l n nh t, nh nh t c a hàm s trên kho ng là . Khi đó, các giá ọ ị ớ ấ ỏ ấ ủ ố ả
tr l n l t là :ị ầ ượ
A . Không có ; . B. ; .
C. ; . D. Không có .
1.2. Tìm giá tr l n nh t – giá tr nh nh t c a hàm s trên m t đo nị ớ ấ ị ỏ ấ ủ ố ộ ạ
Ph ng phápươ
Xét hàm s trên đo n . Tính ố ạ
Tìm các đi m , t i đó ho c không xác đnh.ể ạ ặ ị
Tính
Tìm s l n nh t và s nh nh t trong các s trên. ố ớ ấ ố ỏ ấ ố
Ta có và .
Ví d 2:ụ Giá tr l n nh t và giá tr nh nh t c a hàm s trên l n l t là:ị ớ ấ ị ỏ ấ ủ ố ầ ượ
A. 7 và 2. B. 7 và . C. 7 và 0. D. 7 và .
L i gi iờ ả
Ch n Dọ.
Ta có:
Mà .
Suy ra ; .
Phân tich cac sai lâm dê măc phai cua hoc sinh ( ( )
H c sinh không lo i giá tr .ọ ạ ị
Tính và .
Suy ra ; .
S d ng Casioử ụ
Nh p MODE 7 . ậ.
Start? - End? Step? . K t lu n.ế ậ
Bài t p t ng t :ậ ươ ự
Câu 1. (QG – 2019) Giá tr l n nh t c a hàm s trên đo n b ngị ớ ấ ủ ố ạ ằ
A. .B. .C. .D. .
Câu 2. (QG – 2018) Giá tr nh nh t c a hàm s trên đo n b ngị ỏ ấ ủ ố ạ ằ
A. B. . C. . D. .
Câu 3. (MH – 2018) Giá tr l n nh t c a hàm s trên đo n b ngị ớ ấ ủ ố ạ ằ
A. .B. .C. .D. .
Câu 4. (QG – 2017) Tìm giá tr nh nh t ị ỏ ấ m c a hàm s trên đo n ủ ố ạ
A. B. C. D.
Câu 5. Giá tr nh nh t c a hàm s trên đo n đt t i . Giá tr b ngị ỏ ấ ủ ố ạ ạ ạ ị ằ
A. B. C. D.
4

Câu 6. (QG – 2017) Tìm giá tr nh nh t m c a hàm s ị ỏ ấ ủ ố trên đo n . ạ
A. B. C. D.
Câu 7. (MH – 2017) Tìm giá tr nh nh t c a hàm s trên đo n [2; 4].ị ỏ ấ ủ ố ạ
A. B. C. D.
Câu 8. Cho hàm s . G i , l n l t là giá tr l n nh t và giá tr nh nh t c a hàmố ọ ầ ượ ị ớ ấ ị ỏ ấ ủ
s trên đo n . Tính ?ố ạ
A. . B. . C. . D. .
Câu 9. Giá tr l n nh t c a hàm s trên đo n là:ị ớ ấ ủ ố ạ
A. B. C. D.
Câu 10. Tìm giá tr nh nh t c a hàm s trên đo n .ị ỏ ấ ủ ố ạ
A. .B. .C. .D. .
Câu 11. Tìm giá tr nh nh t c a hàm s trên đo n ị ỏ ấ ủ ố ạ
A. . B. . C. . D. .
Câu 12.
G i là giá tr l n nh t c a hàm s ọ ị ớ ấ ủ ố trên đo n ạ. Khi đó:
A. .B. .C. .D. .
Câu 13. Giá tr l n nh t và giá tr nh nh t c a hàm s trên đo n l n l t làị ớ ấ ị ỏ ấ ủ ố ạ ầ ượ
A. và . B. và . C. và . D. và
Câu 14. Tìm giá tr l n nh t c a hàm s trên đo n ị ớ ấ ủ ố ạ
A. B. C. D.
N u hàm s đn đi u trên thì: ế ố ơ ệ
; .
Ví d 3:ụ Tìm giá tr l n nh t c a hàm s trên đo n ị ớ ấ ủ ố ạ
A. Không t n t iồ ạ B. 0 C. -2 D. 2
L i gi iờ ả
Trên đo n có:ạ
, suy ra hàm s đng bi n trên đo n ố ồ ế ạ
V y ậ
Bài t p t ng t :ậ ươ ự
Câu 1. Tìm giá tr nh nh t c a hàm s trên .ị ỏ ấ ủ ố
A. B. C. D.
Câu 2. Tìm giá tr l n nh t c a hàm s trên đo n .ị ớ ấ ủ ố ạ
A. . B. . C. . D. .
Câu 3. Giá tr l n nh t c a hàm s trên đo n là:ị ớ ấ ủ ố ạ
A. .B. .C. .D.
5
















