
Tiết 28: BÀI TẬP
A. CHUẨN BỊ:
I. Yêu cầu bài:
1. Yêu cầu kiến thức, kỹ năng, tư duy:
Học sinh nắm được dạng bài tập và phương pháp giải bài tập đó.
Rèn luyện kỹ năng nhớ, tính toán, tính nhẩm, phát triển tư duy cho học sinh.
Rèn luyện tính cẩn thận, chính xác, khoa học cho học sinh.
2. Yêu cầu giáo dục tư tưởng, tình cảm:
Qua bài giảng, học sinh say mê bộ môn hơn và có hứng thú tìm tòi, giải quyết
các vấn đề khoa học.
II. Chuẩn bị:
Thầy: giáo án, sgk.
Trò: vở, nháp, sgk và chuẩn bị bài tập.
B. Thể hiện trên lớp:
I. Kiểm tra bài cũ: (4’)
CH: Tìm khoảng lồi, lõm và điểm uốn của hàm số: y = x3 + 6x - 5?
ĐA:
TXĐ: R
y’ = 3x2 + 6 y’’ = 6x
1đ
2 đ

y’’= 0 x = 0
Bảng xét dấu y’’:
x -
0 +
y’’ - 0 +
Đồ thị
Lồi
Lõm
2 đ
5 đ
II. Dạy bài mới:
PHƯƠNG PHÁP tg NỘI DUNG
Hs đọc và nhận dạng bài tập.
Tên của hsố? txđ?
Hãy tính đạo hàm bậc nhất,
bậc hai và xét dấu y’’?
tính lồi lõm và điểm uốn?
12
Bài tập 3: Tìm các khoảng lồi, lõm và điểm uốn
của đồ thị mỗi hsố sau:
b, 4 2
2
4 2
x x
y
Giải:
TXĐ: D = R
y’ = x3 + x
y’’ = 3x2 + 1 > 0 x R
Vậy: Đồ thị lõm trên R và không có điểm uốn.
ĐU
(0;-4)

Hs nhận dạng hsố?
y’ = ?, y’’ = ? Giải phương
trình y’’ = 0? Từ đó, hãy lập
bảng xét dấu y’’?
Hs kết luận tính lồi, lõm và
điểm uốn?
Hs đọc nội dung bài tập?
Để đồ thị nhận (1;1) làm
điểm uốn, ta cần phải có điều
kiện gì?
HS: Để đồ thị nhận (1;1) làm
điểm uốn thì phải có:
9
c, y = 3x5 - 5x4 + 3x - 2
Giải:
TXĐ: D = R
y’ = 15x4 - 20x3 + 3
y’’ = 60x3 - 60x2 = 60x2(x - 1)
y’’ xác định trên R và y’’ = 0
0
1
x
x
Bảng xét dấu y’’:
x - 0 1 +
y’’ - 0 - 0 +
ĐT
lồi
lõm
Bài tập 4:
Tìm a, b để đồ thị của hsố y = x3 - ax2 + x + b
nhận điểm (1;1) làm điểm uốn.
Giải:
Ta có: y’ = 3x2 - 2ax + 1
y’’ = 6x - 2a
Đồ thị nhận (1;1) làm điểm uốn khi
ĐU
(
1;
-
1
)
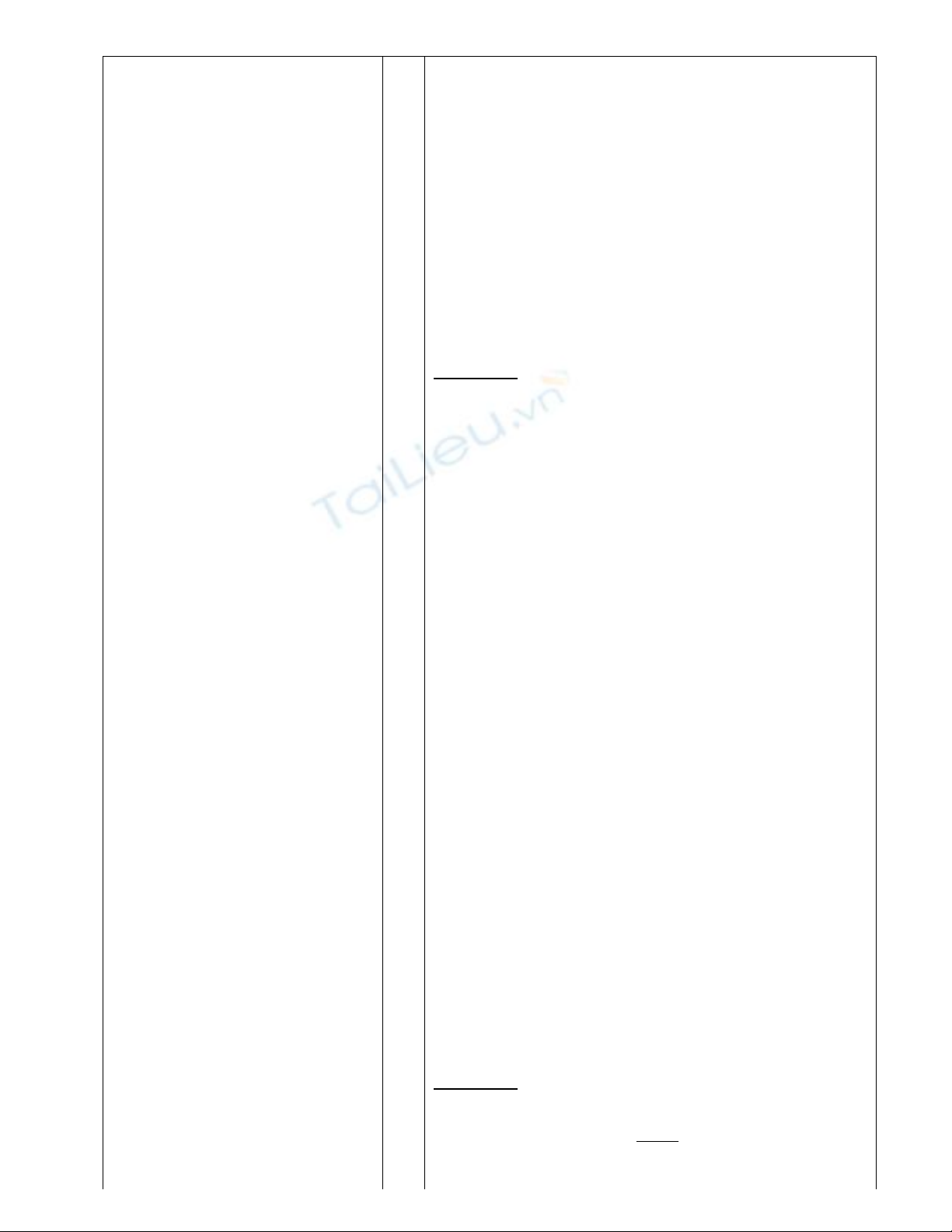
''(1) 0
(1) 1
y
y
và qua x = 1, y’’ đổi
dấu.
Tính y’’? y’’(1) = ? y(1) = ?
Giải hệ, ta tìm được a, b.
Hs đọc.
HS: Để xác định điểm uốn
của một đồ thị, ta phải tính
y’’.
Nhận dạng hsố y’’?
Đồ thị có điểm uốn khi nào?
vầ không có điểm uốn khi
nào?
Hd: Hsố bậc hai có hai
nghiệm phân biệt luôn đổi
dấu khi x đi qua hai nghiệm.
Nếu có một nghiệm hoặc vô
7
12
''(1) 0
(1) 1
6 2 0
1 1 1
3
2
y
y
a
a b
a
b
Vậy: Hsố y = x3 - 3x2 + x + 2 nhận (1;1) làm
điểm uốn.
Bài tập 5:
Tìm a để đồ thị của hsố y = x4 - ax2 + 3
a, Có 2 điểm uốn.
b, Không có điểm uốn.
Giải:
Ta có: y’ = 4x3 - 2ax
y’’ = 12x2 - 2a = 2(6x2 - a)
a, Đồ thị của hsố có điểm uốn khi y’’ = 0 có 2
ngiệm và đổi dấu khi đi qua nghiệm này. Mà y’’
là hsố bậc 2 nên luôn đổi dấu khi đi qua hai
nghiệm.
6x2 - a = 0 có 2 nghiệm a > 0
b, Hsố không có điểm uốn y’’ = 0 vô nghiệm
hoặc có ngiệm kép a ≤ 0
Bài tập 6:
CMR: đường cong 2
1
1
x
y
x
có ba điểm uốn nằm

nghiệm thì hsố không đổi
dấu.
Để cm đồ thị có ba điểm uốn,
ta phải chứng minh điều gì?
HS: Tính y’, y’’ và giải
phương trình y’’ = 0, xét dấu
y’’ từ đó kết luận về điểm
uốn của đồ thị.
trên cùng một đường thẳng.
Giải:
TXĐ: D = R
2 2
2 3
2 2
1 2 2( 1)( 4 1)
' ''
1 1
x x x x x
y y
x x
y’’ xác định trên R
và y’’ = 0
1
2 3
2 3
x
x
x
Bảng xét dấu y’’:
x -
2 3
2 3
1 +
y’’ - 0 + 0 - 0 +
Đồ thị
lồi
lõm
lồi lõm
Hãy tính toạ độ các điểm Từ bảng, ta có toạ độ 3 điểm uốn:
ĐU
1 3
2 3; 4
ĐU
1 3
2 3; 4
ĐU
(1;1)
















