Tiết 57 BÀI TẬP ÔN TẬP HỌC KÌ I.
A. Chuẩn bị:
I. Yêu cầu bài:
1. Yêu cầu kiến thức, kỹ năng, tư duy:
Nhằm giúp học sinh củng cố, ôn luyện các kiến thức về đạo hàm, phương
trình tiếp tuyến, khảo sát hàm số và các bài toán có liên quan đến khảo sát
Thông qua bài giảng rèn luyện cho học sinh kĩ năng khảo sát hàm số, tính
đạo hàm, giá trị lớn nhất, nhỏ nhất của hàm số, kĩ năng tính toán, khả năng tư
duy lô gíc, tư duy toán học dựa trên cơ sở các kiến thức về đạo hàm, khảo sát.
2. Yêu cầu giáo dục tư tưởng, tình cảm:
Qua bài giảng, học sinh say mê bộ môn hơn và có hứng thú tìm tòi, giải
quyết các vấn đề khoa học.
II. Chuẩn bị:
Thầy: giáo án, sgk, thước.
Trò: vở, nháp, sgk và đọc trước bài.
B. Thể hiện trên lớp:
I. Kiểm tra bài cũ: (5’)
CH + Nêu các công thức tính đạo hàm của các hàm số sơ cấp cơ
bản
ĐA (SGK-)
II. Dạy bài mới
PHƯƠNG PHÁP tg NỘI DUNG
Hs xác định dạng bài tập
và phương pháp giải?
học sinh giải?
học sinh giải?
19
Bài 1: Cho hàm số
y a sinx a cosx
Với a>0
a. Tìm TXĐ của hàm số khi a=0
b. Tính y’
c. Tính y2 từ đó suy ra hàm số đạt giá trị lớn
nhất khi
x k2 ,k Z
4
Giải
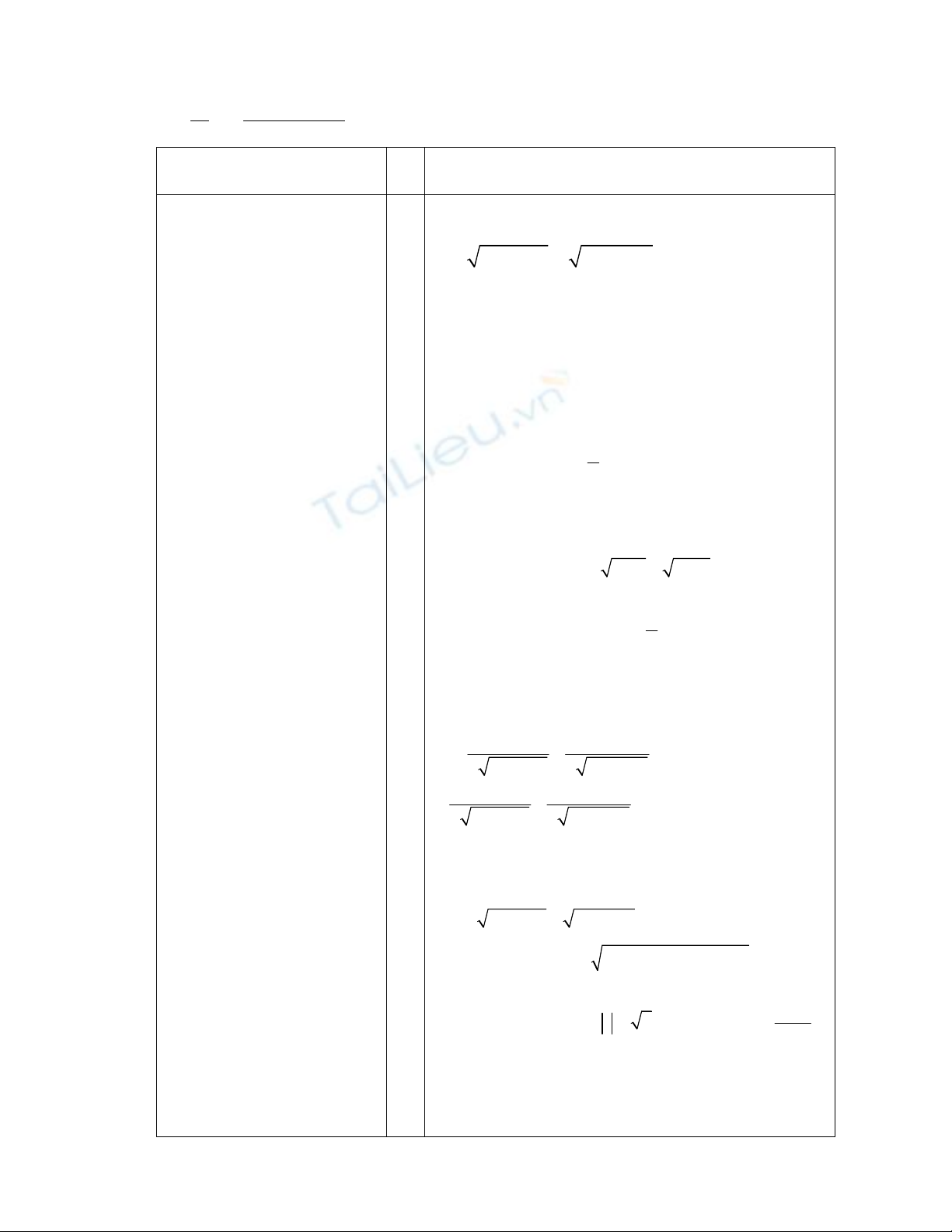
a. Khi a=0 ta có: y
sin x cosx
ĐK: cosx 0
k2 x k2 ,k Z
sin x 0 2
b. Ta có:
a sin x ' a cos x
y'
2 a sin x 2 a cosx
cosx sin x
2 a sin x 2 a cosx
c.Ta có:
2
2
y a sin x a cosx
2a sin x cosx 2 a sin x a cos x
Đặt:
2
t 1
sin x cos x t, t 2 sin x.cos x
2
Để CM môt bất đẳng
thức, ta có những phương
pháp nào?
CM mà sử dụng đạo hàm
là làm như thế nào?
học sinh giải?
20
2
2 2
2
t 1
y 2a t 2 a at
2
1
2a 2 2 a a 2
2
Đẳng thức xảy ra khi t=sinx+cosx=
2
x=/4+k2 (kZ)
Bài 2: Chứng minh các bất đẳng thức
a. ex >1+x với x 0
b. ln(x+1) < x x>0
c. cosx > 1 -
2
x
2
x>0
Giải
a.Xét hàm số: f(x)=ex –(1+x) , x0
Ta có: f’(x)=ex-1 0 x 0 f(0)=0hàm số
f(x) luôn đồng biến trên [0;+) hay x 0: f(x)
f(0)
ex-(1+x) 0 hay ex 1+x x 0 đpcm
b. Xét hàm sô: f(x)=ln(1+x)-x , x 0
Ta có: 1 x
f '(x) 1 0, x 0
1 x 1 x
hàm số f(x) nghịch biến với x 0
f(x) f(0)=0
ln(1+x)-x 0 ln(1+x) x đpcm
c. Xét hàm số: f(x)= cosx +x2/2-1, x>0
Ta có: f’(x)= - sinx + x>0 x>0
Nắm vững cách xét tính
đơn điệu của hsố.
hàm số f(x) đồng biến trên (0; + )
f(x)>f(0)=0 cosx +x2/2-1>0
cosx>1-x2/2 , x>0
III. Hướng dẫn học sinh học và làm bài tập ở nhà:(1’)
- Nắm vững các dạng bài toán liên quan và cách giải các dạng bài toán đó
- áp dụng giải các bài tập 4, 5
III.