Xử lý dữ liệu Tín hiệu số

Chương 33 Chương

BK TP.HCM

BIẾN ĐỔI Z BIẾN ĐỔI Z

T.S. Đinh ĐứcAnh V ũ

FacultyofComputer Science andEngineering HCMC UniversityofTechnology 268, av. LyThuongKiet, District 10, HoChiMinhcity (08) 864-7256 (ext. 5843) Telephone : Fax : (08) 864-5137 Email : anhvu@hcmut.edu.vn http://www.cse.hcmut.edu.vn/~anhvu

Nộidung Nộidung

“ BĐ thuận “ BĐ ngược

§ Biến đổi Z

“ Điểmkhông(Zero) – Điểm cực(Pole) “ Pole vàt/hnhânqu ả trongmi ềnth ờigian “ Mô tả h/tLTI b ằnghàm h ệ thống

§ Cáctínhch ất của BĐ Z § BĐ Z hữu tỉ

ữu tỉ

“ Phương pháptíchphân “ Phương phápkhaitri ểnthànhchu ỗi lũyth ừa “ Phương phápphânrãthànhcác h

§ Biến đổiZ ng ược

“ Tínhch ất “ GiảiPTSP b ằng BĐ Z+

§ Biến đổiZ m ộtphía(Z +)

“ Đáp ứng của hệ “ Đáp ứng tứcth ời, quá độ “ Tính ổn địnhvànhânqu ả

§ Phân tích hệ LTI

2 Biến đổi Z Biến đổi Z

§ Tổngquát

+¥

§ Địnhngh ĩa

ềutr ường hợp(d ựavàocáct/c c ủa BĐ Z) “ Mộtcáchbi ểudi ễnt/hkhác v ề mặttoán h ọc “ Biến đổit/h t ừ miềnth ờigiansang mi ền Z “ Dễ khảosátt/hvàh/ttrongnhi

= (cid:229)

Xzxn z ()( ) n

=-¥

“ Công thức

()( ) z xnX z‹(cid:190)ﬁ

“ Quan hệ

“ Ký hiệu X(z) ≡ Z{x(n)}

Điểmthu ộc mặtph ẳngz “ Biến z

z = a + jbhay z = re jδ

“ Miền hội tụ (ROC){z │ |X(z)| < ∞}

Chỉ quantâmX(z) t ạinh ững điểmz thu ộcROC

3 Biến đổi Z Biến đổi Z

§ Ví dụ

+¥

1 -

)( zX

)( znx

(

)

“ T/h nhânqu ả

(cid:229)

-¥=

1 -

Khi

..(1

zei

)( zX

1 -

1 az

ROC

(cid:222)

1 -

x(n) = anu(n) - (cid:229) =

n ) za

1 - za

: “ T/h phảnnhânqu ả x(n) = –anu(–n–1) +¥ (cid:229)

(cid:229)

)( znx )( zX ( ) - = = -=

-¥=

1 =

1 - zaKhi

( -¥=

1 -

1 - za 1 - za -

..(1 zei a ), )( zX < < -= = 1 1 1 az -

ROC : z a (cid:222) <

• T/h RRTG x(n) đượcxác địnhduynh ất bởibi ểuth ức BĐ Z vàROC c ủanó • ROC củat/hnhânqu ả làph ầnngoài c ủavòngtrònbánkính r củat/hph ảnnhânqu ả làph ầntrong c ủavòngtrònbánkính r

2, trongkhiROC 1

“ Ý nghĩa

4 Biến đổi Z Biến đổi Z

§ ROC củacáct/h

T/h hữu hạn T/h vô hạn

T/h ROC T/h ROC

Img

Mpz\{0} │z│> r2 Nhânqu ả [x(n)=0 n<0] Nhânqu ả (t/h bênph ải) [x(n)=0 n<0]

Mpz\ { ¥} │z│< r1 Phảnnhânqu ả [x(n)=0 n>0] Phảnnhânqu ả (t/hbêntrái) [x(n)=0 n>0]

2 bên 2 bên Mpz\{0, ¥}

+¥

§ BĐ Z mộtphía

+ zX )(

nznx - )(

Vànhkhuyên r1 >│z│> r2

(cid:229)

5 Biến đổi Z Biến đổi Z

§ TíchphânCauchy

1 --

„

1 (cid:242) 2 j C p

1 (cid:236) (cid:237) 0 (cid:238)

kzkx )(

)( zX

§ Biến đổiZ ng ược +¥ (cid:229) -¥= “ Nhân 2 vế với zn–1 “ Tíchphân2 v ế theo đườngcong kínC bao g ốcO thu ộcROC c ủaX(z)

+¥

n 1 --

1 -

)( zzX

)( zkx

(cid:242)

(cid:242) (cid:229)

-¥=

+¥

1 --

1 -

“ Từ

njx )(

2 p=

z C

(cid:242)

= (cid:229) (cid:242) kx )(

-¥=

1 -

(cid:222)

)( nx

)( zzX

“ Áp dụngtíchphânCauchy zzX )(

(cid:242)

1 j 2 p

6 Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

z(cid:190)ﬁ‹ z(cid:190)ﬁ‹

(cid:222)

§ ROC = ROC1 ∩ ROC2 ∩ … ∩ ROCn nx )( § Tuyếntính 1 )( nx 2 n )(

nx )(

n )(

zX )(

z )(

zX )( 1 zX )( 2 z (cid:190)ﬁ‹

ax 1

“ Ví dụ

ROC

n nua )(

z (cid:190)ﬁ‹

zX )( 1

nx )( 1

1 -

x(n) = anu(n) + bnu(–n–1) 1 az

( nub

ROC

)1 (cid:190)ﬁ‹--

)( nx 2

)( zX 2

1 -

1 bz

Do đó

)( nx

)( zX

z (cid:190)ﬁ‹

)( nx 1

)( nx 2

)( zX 1

)( zX 2

1 -

1 az

1 bz

ROC

7 Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

nx )(

zX )(

ROC

z (cid:190)ﬁ‹

§ Co giãntrongmi ền Z

r 1:

r 2

n nxa )(

1 - zaX (

)

(

thuc

hay

phuc

)

z (cid:190)ﬁ‹

a "

(cid:222)

ROC

ra 1

ra 2

Im(z)

j w 0

Re(z)

j w

§ Ý nghĩa a er 0 re

(cid:222)

= )}(

)}({ nxZ n { nxaZ

)( zX ( ) wX

1 - zaw =

)

( ww- 0

Im(w)

1 - zaw =

r/r0

1 r 0

(cid:230) (cid:231)(cid:231) Ł

ω–ω0 Re(w)

(cid:246) jer (cid:247)(cid:247) ł co

Thay

bien

quay

mpz

(cid:219)

gian

(cid:236) (cid:237) (cid:238)

1 (cid:252) (cid:253) 1 (cid:254)

w=a–1z

9 Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

)( nx

)( zX

ROC

z (cid:190)ﬁ‹

§ Đảoth ờigian

1: r

r 2

1 -

)

( nx

( zX

ROC

(cid:190)ﬁ‹-

(cid:222)

1 r 2

1 r 1

“Ý nghĩa

• ROCx(n) làngh ịch đảo củaROC x(–n) • Nếu z0 ˛ ROCx(n), 1/z0 ˛ ROCx(–n)

nx )(

zX )(

z(cid:190)ﬁ‹

§ Vi phântrongmi ền Z

)( z

)( nnx

z -(cid:190)ﬁ‹

(cid:222)

10 Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

§ Tíchch ập

nx )( 1 nx )( 2

zX )( 1 zX )( 2

(cid:222)

nx )(

*)(

zX )(

zXzX )(

)(

z(cid:190)ﬁ‹ z(cid:190)ﬁ‹ z (cid:190)ﬁ‹

nx 1

nx )( 2

§ Tínhtíchch ập của2 t/hdùngphép BĐ Z

“ Xác định BĐ Z của2 t/h

Miềnth ờigian ﬁ miền Z X1(z) = Z{x1(n)} X2(z) = Z{x2(n)}

“ Nhân 2 BĐ Z vớinhau X(z) = X1(z)X2(z)

“ Tìm BĐ Z ngược củaX(z)

Xử lýtrongmi ền Z

x(n) = Z-1{X(z)} MiềnZ ﬁ miềnth ờigian

11 Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

§ Tương quan

z(cid:190)ﬁ‹ z(cid:190)ﬁ‹

)( nx 1 nx )( 2

)( zX 1 zX )( 2

1 -

l )(

)(

)

(

z )(

zXzX (

)(

)

(cid:190)ﬁ‹-

lnxnx 1 2

r xx 21

xx 21

= (cid:229)

-¥=

§ Việctính t ươngquangi ữa2 t/h đượcth ựchi ện dễ dàngnh ờ BĐ Z § Ví dụ: xác địnhchu ỗi tự tươngquan c ủat/hx(n) = a nu(n) (|a| < 1)

)( nx

n )( nua

)( zX

ROC

z (cid:190)ﬁ‹

( zX

1 =- )

1 az 1 - : ROC z <

1 az -

1 -

)( zXzX (

)

)( zRxx

1 -

1 az

( za

)

1 - 1 a 1 az -

1 z +

ROC

1 a

)( l

l ¥<<-¥

r xx

1 a -

(cid:222)

12 Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

§ Nhân 2 chuỗi

z(cid:190)ﬁ‹ z(cid:190)ﬁ‹

)( nx 1 nx )( 2

zX )( 1 zX )( 2

1 -

nx )(

)(

zX )(

XvX )(

(

)

z (cid:190)ﬁ‹

nxnx )( 1

(cid:242)

(cid:222)

z v

bao

dong

quanh

goc

thuoc

chung

1 j 2 p ROC

v )/1(

XvavXcua )( 1

§ Cáchxác địnhmi ền hội tụ tu

hoi

vX )( 1

r u 1

r l 1

hoi

zX )( 2

r 2

hoi

vzX )/(

(cid:222)

r 2

z v

hoi

zXdoDo , )(

rr l 21

rr u 1 2

13 Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

ịđầ u

§ Địnhlýgiátr

"n<0]

“ Nếux(n) nhânqu ả [x(n) = 0 (cid:222)

zX )(

)0(

lim z ¥ﬁ

nx )(

zX )(

z(cid:190)ﬁ‹

§ Phức hợp

n )(*

z(cid:190)ﬁ‹

“ Phầnth ực

Re{

nx )}(

[

zX )(

*)]

z (cid:190)ﬁ‹

1 2

“ Phần ảo

1 z z Im{()}[()*(*)] xnXzX ‹(cid:190)ﬁ j 2

14 Biến đổiZ h ữu tỉ –zero & pole Biến đổiZ h ữu tỉ –zero & pole

§ Zero của BĐ X(z): cácgiátr ị z saochoX(z) = 0 § Pole của BĐ Z: cácgiátr ị củaz saochoX(z) = ¥ § ROC khôngch ứa bất kỳ pole nào § Ký hiệutrênmpz: zero –vòngtròn(o) vàpole –ch

)( zX

zX )(

1 z

1 9.01 -

ữ thập(x) z - 1 - -

15 Biến đổiZ h ữu tỉ –zero & pole Biến đổiZ h ữu tỉ –zero & pole

§ Biến đổiZ d ạng hữu tỉ

“ Rất hữuích để phântích h ệ LTI RRTG “ Việcxéttínhch ấthay thi ết kế hệ cótínhch ấtnào đó ﬁ chỉ cần

quantâmtrên v ị trí củacác điểmzero-pole

zb k

1 -

(cid:229)

§ Cáccáchbi ểudi ễn “ Dạng mũ âm

)( zX

k = M

1 -

)( zN )( zD

b 0 a

+ +

L + L +

+ +

zb 1 za 1

zb M za N

za k

(cid:229)

1 -

MN -

“ Dạng mũ dương

zX )(

1 -

b 0 a 0

b 1 b 0 a 1 a

Mb b 0 a N a

(cid:213)

MN -

“ DạngZero-Pole

( z z ) -

1 k = N

(cid:213)

1 =

G ”

Gz Gz zX )( = = z z z 2 p z M p z ( z ( )( )( z ( z ( ) ) - - - - - - ) K ) K z 1 p 1 ( z p ) -

16 Biến đổiZ h ữu tỉ –zero & pole Biến đổiZ h ữu tỉ –zero & pole

MN -

zX )(

z z

z 2 p

z M p

§ Dạng hữu tỉ từ zeros-poles z ( z (

)( )(

z ( z (

) )

- -

) K ) K

z 1 p 1

§ VD: Tìm dạng hữu tỉ và vẽ giản đồ zero-pole choX(z):

“ G: độ lợi(gain)

%Tim Huuti, zplane: zpm.m %---------------------------------- M=8; a=0.8; p=zeros(M,1); z=zeros(M,1); for k=1:M,

z(k,1)=a*exp((j*2*pi*k)/M);

end; [num den] = zp2tf(z,p,1); disp(num); disp(den); zplane(z,p);

Zeros: Zk=0.8ej2πk/M , k=1..M Poles: M pole tại 0

17 Biến đổiZ h ữu tỉ –zero & pole Biến đổiZ h ữu tỉ –zero & pole

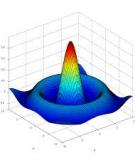
§ Mô tả hình họcchoX(z)

“ |X(z)| làhàmth ực, dương củabi ếnz

ﬁ bề mặt

“ Zeros: các đỉnh dương, cao “ Poles: các đỉnhâm, th ấp “ VD:

)( zX

1 19.01 -

Dạnghình h ọcdùngMatlab

ezmesh('a', 'b',

'0.1*log10(abs(1/(1 -0.9*(a+j*b)^-1)))', [-2,2,-2,2]);

18 Biến đổiZ h ữu tỉ Biến đổiZ h ữu tỉ

§ Vị trípole vàhànhvi c ủat/hnhânqu ả ở miềnth ời

gian “Vị trípole ảnh hưởngtínhch ất bị chận, phân kỳ củatín

hiệunhânqu ả ở miềnth ờigian

“Vị trípole quy ết địnhtính ổn định của hệ thốngnhânqu ả “Tínhch ất củatínhi ệu ở miềnth ờigian, trongtr ường hợp pole nằmngoàihay tronghay trên vòngtròn đơn vị qua nhữngví d ụ sau

19 Biến đổiZ h ữu tỉ – Vị trípole Biến đổiZ h ữu tỉ – Vị trípole

20 Biến đổiZ h ữu tỉ – Vị trípole Biến đổiZ h ữu tỉ – Vị trípole

21 Biến đổiZ h ữu tỉ – Vị trípole Biến đổiZ h ữu tỉ – Vị trípole

p=1.2e±jπ/4

p=0.8e±jπ/4

p=e±jπ/4

p=0.8e±jπ/4

22 BĐ Z hữu tỉ –Hàmh/t c ủa hệ LTI BĐ Z hữu tỉ –Hàmh/t c ủa hệ LTI

§ VD

x(n) y(n)

Hệ thốngLTI h(n)

“ h(n) = (1/2)nu(n) “ x(n) = (1/3)nu(n)

y(n) = x(n)*h(n)

zH )(

1 -

Y(z) = X(z) H(z)

zX )(

1 -

1 1 2 1 1 3

“ TínhX(z) vàH(z) “ Xác địnhY(z) “ Tìmy(n) b ằngcáchtính BĐ Z ngược củaY(z)

§ Xác địnhy(n)

zY )(

(cid:222)

1 -

1 1 2

1 1 3

)( zH

nznh - )(

(cid:229)

)( zY zX )(

-¥=

1 -

(

6 )(2

§ Tìm đáp ứng đơn vị

ền Z ềnTG

“ H(z): đặctr ưngchoh/ttrongmi “ h(n): đặctr ưngchoh/ttrongmi

§ Hàmh/t: H(z)

23 BĐ Z hữu tỉ –Hàmh/t c ủa hệ LTI BĐ Z hữu tỉ –Hàmh/t c ủa hệ LTI

§ Hàm hệ thống của hệ LTI mô tả bởiPTSP TT HSH

)( ny

( knya

)

( knxb k

(cid:229)

1 =

x(n) y(n) b0 + +

“ Hệ pole-zero

Z-1 Z-1

(cid:229)

a1 b1 zb k + +

0 N

(cid:229)

1 =

“ Hệ toànzero

• ak = 0

kM -

)( zH ” = )( zY zX )( Z-1 Z-1 1 + za k a2 b2 + +

k - =

(cid:229)

1 ≤ k ≤ N M 1 (cid:229) M z

aN–1 )( zH = zb k zb k bM–1 + +

• FIR “ Hệ toànpole

• bk = 0

1 ≤ k ≤ M zb 0

Z-1 Z-1 aN bM

kN -

a zH )( 1 = = ” b 0 N

(cid:229)

1 =

• IIR

1 + za k za k

24 Biến đổiZ ng ược Biến đổiZ ng ược

§ Phương pháptíchphântr ựcti ếp

“ Địnhlýth ặng dư Cauchy

• Nếu đạohàmdf(z)/dz t ồn tạitrênvàtrongbao đóngC và n ếuf(z)

( zf

)

z z

bên bên

trong ngoài

C C

khôngcópole t ạiz = z 0

(cid:242) j C

1 2 p

)( zf z z -

(cid:236) (cid:237) (cid:238)

• Tổngquát, n ếu đạohàm b ậck+1 c ủaf(z) t ồn tạivàf(z) khôngcópole

1 -

bên

trong

)( zf 1 k -

(

)!1

1 -

zz =

tạiz = z 0

(cid:242)

(

zf )( z ) -

1 j 2 p

bên

ngoài

dz 0

(cid:236) (cid:239) (cid:237) (cid:239) (cid:238)

• Vế phải của2 bi ểuth ứctrên g ọilàth ặng dư của cực tạiz = z 0

26 Biến đổiZ ng ược Biến đổiZ ng ược

đóngC và đath ứcg(z) cócác

§ Giả sử f(z) khôngcópole trongbao

(cid:242)

)( zf )( zg

nghiệm đơnriêngbi ệt z1, z2, …, zn trong C 1 2 j p

1 2 j p

)( zA i z z -

1 =

Ø (cid:242) (cid:229) Œ º

ø dz œ ß

1 (cid:229) (cid:242) j 2 p

)( zA i z z -

1 =

(

)

zA )( i

)

zf )( )( zg

( zA i

(cid:229)

1 =

§ Biến đổiZ ng ược

1 -

)( nx

)( zzX

(cid:242)

1 j 2 p

1 -

cua

tai

zzX )(

]

(cid:229)

cac

pole

thang [ trong C }{ z i

1 -

(

)

)( zzXz i

(cid:229)

zz =

: Thặng dư

27 Biến đổiZ ng ược Biến đổiZ ng ược

-1

1 -

1 az

)( nx

1 - dz

1 -

(cid:242)

)( zX n z az -

1 2 j p

z -

§ Ví dụ: tìm BĐ Z ngược của 1 (cid:242) 1 2 j p “ C: vòngtrònbánkínhr > |a| 1. n ≥ 0: zn khôngcópole trongC. Pole bênngoàiC làz = a

(cid:222) x(n) = f(z0) = an

)1( =-

(cid:242)

zz (

)

2. n < 0: zn cópole b ậcn t ạiz = 0 (bêntrongC) 1 1 z -

1 -

1 2 j p

az =

)2( -

(cid:242)

)

(

d dz

1 2 z

1 2 j p

1 az -

(cid:230) (cid:231) Ł

(cid:246) (cid:247) ł

az =

“ Cóth ể CM đượcx(n) = 0 khin < 0

(cid:222) x(n) = anu(n)

28 Biến đổiZ ng ược Biến đổiZ ng ược

§ PP khaitri ểnthànhchu ỗitheobi ếnz và z –1 ất của BĐ Z, nếuX(z) được

“Dựavàotínhduynh khaitri ểnthành

zX )(

n zc

(cid:229)

-¥=

thì

x(n) = cn "n

“NếuX(z) h ữu tỉ, phépkhaitri ển đượcth ựchi ện

bằngphépchia • PP nàych ỉđượ cdùng để xác địnhgiátr ị vài mẫu đầu

củat/h

29 Biến đổiZ ng ược Biến đổiZ ng ược

)( zX

§ Ví dụ: xác địnhx(n) t ừ

5.0

1 1 - +

5.11 - Vớia) ROC |z| >1 vàb) ROC |z| < 0.5

• x(n) làt/hnhânqu ả

1 -

)( zX

1 +=

L+

3 2

7 4

15 8

5.0

1 1 - +

5.11 -

x(n) = {1, 3/2, 7/4, 15/8, …}

(cid:222)

• x(n) làt/hph ảnnhânqu ả

zX )(

L+

5.0

1 1 - +

5.11 -

x(n) = {…, 14, 6, 2, 0, 0}

(cid:222)

30 Biến đổiZ ng ược Biến đổiZ ng ược

§ PP khaitri ểnphân s ố cục bộ vàtra b ảng

“ Nguyên tắc

“ Từ dạng hữu tỉ

)( zX

)( zN zD )(

+ +

zb M - za N

zb 1 1 - za 1

(

)

NM -

zX )(

1 - L +

c 0

zc 1

NM -

zN )( 1 )( zD

1 -

• NếuX(z) đượcbi ểudi ễnX(z) = a 1X1(z) + a2X2(z) + …+ a kXk(z) thìx(n) = a 1x1(n) + a2x2(n) + …+ a kxk(n) L + L +

b 0 1 • X(z) là hợp lệ nếu aN≠0 vàM= N, chia đath ức đểđư a về zN )( )( zD )( zN )( zD

1 -

MN -

)( zX = = • Giả sử X(z) hợp lệ b 0 1 + + L + L + + + zb 1 1 - za 1

MN -

1 -

“ Phương pháp

zb 0 = + N + 1 - z + L L + zb M - za N zb M a + zb 1 za + 1

N zb M a +

zb 0 = + N + 1 - )( zX z z zb 1 + L + za 1

+ L • Khaitri ểnphân s ố cục bộ • Tra bảng để xác định BĐ Z ngược của từngphân s ố

31 Biến đổiZ ng ược Biến đổiZ ng ược

zN + a1zN-1+…+aN = 0

§ Khaitri ểnphân s ố cục bộ “ Tìmpole b ằngcáchgi ảiPT (giả sử cácpole: p 1, p2, …, pN) “ Pole đơnriêngbi ệt =

+ + L + z z A 2 p - A N p -

kpz =

z ( )( zX z - • Xác định Ak = A k A 1 z p - 1 ) )( zXp k z

• Cácpole liên h ợpph ức sẽ tạoracác h ệ số liên hợpph ứctrongkhaitri ển

* thì A2 = A1

“ Pole kép

(i.e. nếu p2 = p1

+ = + L + + L + + L + )( zX z z z z ( z ) ) ( z z • Giả sử pole pk kép bậc l A 2 p - A 1 k p - A 2 k p - A lk p - A N p - A 1 p - 1

l )( zXp

• Xác định Aik

kpz =

,...,2,1 i l = = A ik ) ( l i p d dz ) k z 1 ()! - - Ø - ( z Œ º ø œ ß

32 Biến đổiZ ng ược Biến đổiZ ng ược

§ Tìm BĐ Z ngược của từngphân s ố cục bộ

1 -

“ Nếucácpole đơnriêngbi ệt zX )( = + L ++ A 1 A 2 A N 1 - - 1 zp 1 1 zpz - 2 1 zpz N

1 -

) ( ROC : z ( nhân qua ) > p k Z = do nu )( n 1 ) nu ( )1 ROC : z ( phan nhân qua ) - - -- < 1 zp k p k p ( k p k

(

n 2

n nupA )() N

n nu )(])

)

[

Nên (cid:236) (cid:237) (cid:238) nx )( (cid:252) (cid:253) (cid:254) n pA 11 (cid:236) (cid:237) (cid:238) pA 2

* pA ( k

* k

pA ( k

nx )( k

j a k

“ Nếucó2 pole liên h ợpph ức, cóth ể kết hợp2 pole đó +

j b k

= A k eA k Nếu thì

1 -

p = er k (cid:236) (cid:239) (cid:237) (cid:239)(cid:238)

* A k

n rA k k

1 -

Z 2 cos( )() nu neu ROC : z p + = > = A k n + ab k r k 1 1 - - 1 zp k 1 * zp k (cid:236) (cid:237) (cid:238) (cid:252) (cid:253) (cid:254)

n )( nunp

21 - )

“ Nếucópole kép : ROC z p Z = > 1( pz pz - (cid:236) (cid:237) (cid:238) (cid:252) (cid:253) (cid:254)

33 Biến đổiZ ng ược Biến đổiZ ng ược

§ Xác địnhbi ểuth ứckhaitri ển của

1 2

)

)( zX

2 p

2 zX ( z

A -

1 2 A -

1 z + 1 - 5.0 z +

1 2

3 2

1 2

3 2

zX )(

1 -

zX )( z

(

A 1 +

A 2 z -

A 3 )1 -

1 1)(

21 - )

A 3

A 2

A 1

1 2

3 4

1 4

34 Biến đổiZ ng ược Biến đổiZ ng ược

ươngsau)

“ Dùngtrongvi ệchi ệnth ựccách/tRRTG (cácch “ Giả sử có BĐ Z đượcbi ểudi ễn (đểđơ ngi ản a0≡1)

1 -

§ Phânrã BĐ Z hữu tỉ

(cid:229)

(cid:213)

1( ) - zz k zb k

1 k = N

0 N

1 -

)( zX = = b 0

(cid:229)

(cid:213)

1 =

“ NếuM ≥ N, X(z) cóth ểđượ cbi ến đổithành

NM -

zX )(

z )(

zc k

= (cid:229)

“ Nếu Xpr(z) cócácpole đơnriêngbi ệt, Xpr(z) đượcphânrãthành

z )(

A 1

1 zp 1

1 zp N

1 zp 2 “ Nếu Xpr(z) cónghi ệmph ức(liên h ợp), cácnghi ệmliên h ợpnày đượcnhóm l ại để

tránh tạora h ệ số phức

Re(

)

a 1

với

Re( 2

) *

A pz

A * zp

zb 1 1 +

Re(

)

b 0 =

b + 0 - za 1

za 2

b 1

(cid:236) (cid:237) (cid:238)

1 + 1( ) - za k zp k

35 Biến đổiZ ng ược Biến đổiZ ng ược

§ Tóm lại

NM -

K 1

zX )(

zc k

1 -

(cid:229)

1 =

b k za k

b zb + k k 0 1 1 - za + k 1

za k 2

KK +

với

36 Biến đổiZ ng ược Biến đổiZ ng ược

§ Phânrã BĐ Z hữu tỉ

“ X(z) cóth ểđượ cbi ểudi ễn dưới dạngtích “ Cácpole ph ức(liên h ợp) vàcáczero ph ức(liên h ợp) được kết hợp

1 -

2 -

1 -

để tránh hệ số phứcchophânrã c ủaX(z) 1 - ) 1 - )

1)( 1)(

1( - 1( -

1 + 1 +

+ +

- -

zb k 2 za 2 k

zz k zp k

)

a 1 k

trong

đó

và

zb k 1 za 1 k z Re( 2 z

2 -= a

p Re( 2 p

-= b 2

* zz k * zp k b (cid:236) 1 k (cid:237) (cid:238)

(cid:236) (cid:237) (cid:238)

“ Đểđơ n giản, choM = N, X(z) đượcbi ểudi ễnthành

1 -

2 -

K 1

)( zX

b 0

1 -

(cid:213)

1 1

1 + 1 +

+ +

1 =

zb 1 k za 1 k

zb 2 k za 2 k

trong

đó

1 = =

zb k za k KK + 1

37 Biến đổiZ m ộtphía Biến đổiZ m ộtphía

§ Giớithi ệu

“ Trong kỹ thuật: tác độngth ường bắt đầu từ thời điểm n0 nào đó. Đáp ứng cũngth ường bắt đầu từ n0 vàcácth ời điểmsau n 0, với điềuki ện đầunào đó

“ Biến đổiZ m ộtphía(Z +) chỉ quantâm đếnph ầntínhi ệux(n), n ≥0

§ Địnhngh ĩa

+ zX )(

nznx - )(

”

(cid:229)

nx )(

zX )(

+(cid:190)ﬁ‹

Z+{x(n)}

và

§ Ký hiệu § Đặctính

“ Z+{x(n)} khôngch ứathôngtin c ủax(n) khi n < 0 “ BĐ Z+ chỉ làduynh ất đối vớit/hnhânqu ả “ Z+{x(n)} = Z{x(n)u(n)} • ROC bênngoàivòngtròn • Khôngxét đếnROC khitính BĐ Z+

38 Biến đổiZ m ộtphía Biến đổiZ m ộtphía

§ Tínhch ất

“ Cáctínhch ất của BĐ Z đều đúngcho BĐ Z+, ngoạitr ừ tínhch ất dịch

theoth ờigian

“ Dịchtheoth ờigian

nx )(

zX )(

+(cid:190)ﬁ‹

knx (

)

[

+ zX )(

]

(cid:190)ﬁ‹-

znx ( ) -

• Trễ

(cid:229)

1 =

§ Nếux(n) làt/hnhânqu + knx (

)

ả, tacó k - zXz )(

(cid:190)ﬁ‹-

1 -

knx (

)

k zXz )(

[

znx )(

]

(cid:190)ﬁ‹+

• Nhanh

(cid:229)

“ Địnhlýgiátr

(

+ zX )(

ị cuốicùng lim)( nx lim = 1 n ¥ﬁ ﬁ

• Giới hạn tồn tại nếuROC c ủa(z-1)X +(z) chứavòngtròn đơn vị

39 Biến đổiZ m ộtphía Biến đổiZ m ộtphía

§ GiảiPTSP

“ Dùng BĐ Z+ để giảiPTSP v ới điềuki ện đầukhác 0 “ Phương pháp

“ Ví dụ: xác định đáp ứng bước của hệ y(n) = ay(n–1) + x(n) (|a|< 1)

với đ/k đầu y(–1) = 1

+ zX )(

1 -

• Xác địnhPTSP c ủa hệ • Tính BĐ Z+ cả 2 vế PTSP để biến đổinóthànhPT đại số trongmi ền Z • GiảiPT đại sốđể tìm BĐ Z củat/hmongmu ốn • Tìm BĐ Z ngược để xác địnht/htrongmi ềnth ờigian

+ )( zY

(cid:222)

1 -

a az

1 z -

)( ny

)( nu

)() nu

1 1 az - 1 n + 1 a - 1 -

1 -

Y+(z) = a[z–1Y+(z) + y(–1)] + X+(z) 1 z -

40 Phântích h ệ LTI Phântích h ệ LTI

§ Tìm đáp ứng củat/hx(n) đối với mộth/tLTI

“ Biết đáp ứngxung đơn vị h(n)

x(n) y(n) Hệ LTI

)( ny

)

( knya k

( knxb k

1 Ghiph ươngtrìnhvào-ra

(cid:229)

1 =

PhươngtrìnhSP

2 Biến đổiZ hai v ế

Y(z) = H(z)X(z)

3 Biến đổiZ ng ược(PP: phânrã)

Đáp ứngy(n)

41 Phântích h ệ LTI Phântích h ệ LTI

zH )(

zX )(

và

§ Đáp ứng củah/tpole-zero v ớihàmh/t h ữu tỉ zB )( )( zA

zN )( )( zQ

“ Giả sử

zY )(

zXzH )( )(

zNzB )( )( zQzA )( )(

“ Nếuh/tngh ỉ (tứcy(-1) = y(-2) = …= y(-N) = 0)

)

( zY

(cid:222)

(cid:229)

• H/t cócácpole đơn p1, p2, …, pN vàX(z) cócácpole đơn q1, q2, …, qL • pk ≠ qm (k = 1, …, N vàm = 1, …, L) • Khôngth ểướ c lượcgi ữaB(z)N(z) vàA(z)Q(z) A k zp k

Q k zq k

)( ny

)

)( nu

)

)( nu

“ Giả sử

( pA k

( qQ k

(cid:229)

1 =

“ Biến đổing ược =

Đáp ứng tự nhiên Đáp ứng cưỡng bức

ường hợpX(z) vàH(z) cópole chungho ặc “ Cóth ể tổngquáthoátrongtr

pole bội

42 Phântích h ệ LTI Phântích h ệ LTI

§ Tìm đáp ứng củat/hx(n) đối với mộth/tLTI có đ/k đầu

“ Biết đáp ứngxung đơn vị h(n) “ Biếtcác đ/k đầu củah/t x(n)

y(n) Hệ LTI

1 Ghiph ươngtrìnhvào-ra

PhươngtrìnhSP

2 Biến đổi Z+ hai vế

zi(z) và Y+

zs(z)

Cóth ể táchra Y + Y+(z) = H+(z)X+(z)

3 Biến đổiZ ng ược, (PP: phânrã)

Đáp ứng: y(n) Cóth ể táchra y zi(n) và yzs(n)

43 Phântích h ệ LTI Phântích h ệ LTI

“ Chot/hx(n) nhânqu ả vàcác đ/k đầuy(-1), y(-2), …, y(-N)

§ Đáp ứng củah/tpole-zero v ới đ/k đầukhác 0

(cid:229)

1 =

“ BĐ Z+ cả 2 vế và X+(z) = X(z)

k zb

k za

(

) zn

(cid:229)

)( z

)( zX

0 N

k za

(cid:229)

)( zXzH )(

(

k za

) zn

-”

)( zN 0

(cid:229)

)( zN 0 )( zA

“ Đáp ứng gồm2 ph ần

(côngth ứcph ầntr ước)

Yzs(z) = H(z)X(z)

• Đáp ứngtr ạngtháikhông • Đáp ứngkhôngngõnh ập(p 1, p2, …, pN làpole c ủaA(z))

)( ny ( knya ) ) -= - + - ( knxb k

Z (cid:190)ﬁ‹

(cid:229)

1 =

• Do

y(n) = yzs(n) + yzi(n)

)

ny (

nu (

)

(

)

(cid:222)

' pA ( k

qQ ( k

' k

(cid:229)

(cid:229) • Đ/k đầuch ỉ làmthay đổi đáp ứng tự nhiên củah/tthôngqua h ệ số co giãn

) )( nu = = )( zY zi )( ny zi ( pD k )( zN 0 )( zA

44 Phântích h ệ LTI Phântích h ệ LTI

§ Đáp ứng tự nhiên

)( n

)

)( nu

( pA k

(cid:229)

1 =

§ Đáp ứng cưỡng bức

)( nu

)

)( n

1 =

“ Khi │pk│< 1 ("k), ynr(n) tiệm cận về 0 khin → ¥ : đáp ứngnh ấtth ời ( qQ k

(cid:229) k “ Khit/hnh ậplàt/hsin, cácpole q

k nằmtrênvòngtròn

đơn vị vàcác đáp

§ Tínhnhânqu ả và ổn địnhtrênH(z)

ứng cưỡng bức cũngcó d ạngsin: đáp ứng đều

“ Nhân quả

: nhânqu ả : nhânqu ả : cóROC làngoàivòngtrònbánkínhR nào đó

: ổn định : khả tổngtuy ệt đối : cóROC ch ứavòngtròn đơn vị

LTI (cid:243) h(n) (cid:243) H(z) “ Ổn định LTI (cid:243) h(n) (cid:243) H(z) “ Nhân quả và ổn định

LTI nhânqu ả

: ổn định : tất cả cácpole n ằmtrongvòngtròn đơn vị (cid:243) H(z)

45 Phântích h ệ LTI Phântích h ệ LTI

§ Đáp ứng đềuvàti ệm cận

“ Xác định đáp ứng đềuvàti ệm cận củah/tmô t ả bởiPTSP

y(n) = 3y(n–1) + x(n) khit/hnh ậplà x(n) = 2sin(πn/4)u(n) H/t có đ/k đầu bằng0.

§ Ổn địnhvànhân qu ả

“ Choh/tLTI được đặctr ưng bởihàmh/t

zH (

)

4 1

- - z

2 3

3 5.3

5.1

1 1 2

z + Đặc tả ROC của H(z) vàxác địnhh(n) trongcác tr ường hợp

§ Ổn định của h/t bậc 2

• H/t ổn định • H/t nhân quả • H/t phản nhân quả

Tín hiệu số - Xử lý dữ liệu - Chương 3

Tín hiệu số - Xử lý dữ liệu. Tiến sĩ: Đinh Đức Anh Vũ.Chương 3: Biến đổi Z

Chủ đề:

BK TP.HCM

BIẾN ĐỔI Z BIẾN ĐỔI Z

FacultyofComputer Science andEngineering HCMC UniversityofTechnology 268, av. LyThuongKiet, District 10, HoChiMinhcity (08) 864-7256 (ext. 5843) Telephone : Fax : (08) 864-5137 Email : anhvu@hcmut.edu.vn http://www.cse.hcmut.edu.vn/~anhvu

Nộidung Nộidung

2

Biến đổi Z Biến đổi Z

3

Biến đổi Z Biến đổi Z

4

Biến đổi Z Biến đổi Z

(cid:229)

5

Biến đổi Z Biến đổi Z

(cid:242)

6

Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

7

Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

9

Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

10

Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

11

Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

12

Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

(cid:242)

13

Biến đổiZ –Tínhch ất Biến đổiZ –Tínhch ất

14

Biến đổiZ h ữu tỉ –zero & pole Biến đổiZ h ữu tỉ –zero & pole

15

Biến đổiZ h ữu tỉ –zero & pole Biến đổiZ h ữu tỉ –zero & pole

16

Biến đổiZ h ữu tỉ –zero & pole Biến đổiZ h ữu tỉ –zero & pole

17

Biến đổiZ h ữu tỉ –zero & pole Biến đổiZ h ữu tỉ –zero & pole

18

Biến đổiZ h ữu tỉ Biến đổiZ h ữu tỉ

19

Biến đổiZ h ữu tỉ – Vị trípole Biến đổiZ h ữu tỉ – Vị trípole

20

Biến đổiZ h ữu tỉ – Vị trípole Biến đổiZ h ữu tỉ – Vị trípole

21

Biến đổiZ h ữu tỉ – Vị trípole Biến đổiZ h ữu tỉ – Vị trípole

22

BĐ Z hữu tỉ –Hàmh/t c ủa hệ LTI BĐ Z hữu tỉ –Hàmh/t c ủa hệ LTI

23

BĐ Z hữu tỉ –Hàmh/t c ủa hệ LTI BĐ Z hữu tỉ –Hàmh/t c ủa hệ LTI

24

Biến đổiZ ng ược Biến đổiZ ng ược

(cid:242) j C

(cid:242)

26

Biến đổiZ ng ược Biến đổiZ ng ược

27

Biến đổiZ ng ược Biến đổiZ ng ược

(cid:242)

(cid:242)

28

Biến đổiZ ng ược Biến đổiZ ng ược

(cid:229)

29

Biến đổiZ ng ược Biến đổiZ ng ược

30

Biến đổiZ ng ược Biến đổiZ ng ược

31

Biến đổiZ ng ược Biến đổiZ ng ược

32

Biến đổiZ ng ược Biến đổiZ ng ược

33

Biến đổiZ ng ược Biến đổiZ ng ược

34

Biến đổiZ ng ược Biến đổiZ ng ược

35

Biến đổiZ ng ược Biến đổiZ ng ược

(cid:229)