Bản quyền windows 8, windows 7, Antivirus giá rẻ http://buykeysoft.blogspot.com
Chương 3.
Chương 3: Hiểu.
Câu 1
Nếu G = (V,E) là một đồ thị vô hướng thì
A)
Số đỉnh bậc lẻ và số đỉnh bậc chẵn là một số chẵn
B)
Số đỉnh bậc chẵn là một số chẵn
C)
Số đỉnh bậc lẻ là một số chẵn
D)
Số đỉnh bậc lẻ là một số lẻ
Đáp án
C
Câu 2
Những đơn đồ thị vô hướng nào dưới đây tồn tại nếu bậc của các đỉnh lần
lượt là
A)
1, 4, 3, 2, 5, 6.
B)
2, 1, 5, 2, 3, 3.
C)
2, 4, 3, 4, 3, 2.
D)
1, 4, 3, 2, 2, 3.
Đáp án
C
Câu 3
Đơn đồ thị vô hướng nào dưới đây tồn tại nếu bậc của các đỉnh lần lượt là
A)
1, 2, 3, 4, 5.
B)
0, 1, 2, 2, 3.
C)
3, 4, 3, 4, 3.
D)
1, 2, 3, 4, 7.
Đáp án
B
Câu 4
Đồ thị liên thông nào trong các đồ thị dưới đây là đồ thị Euler nếu số bậc của
các đỉnh lần lượt là
A)
4, 2, 1, 4, 4
B)
2, 4, 2, 4, 2
C)
4, 2, 1, 3, 4
D)
5, 2, 4, 4, 4
Đáp án
B
Câu 5
Đồ thị liên thông nào trong các đồ thị dưới đây là đồ thị nửa Euler nếu số bậc
của các đỉnh lần lượt là
A)
2, 4, 1, 2, 6
B)
3, 4, 4, 2, 4
C)
1, 4, 2, 5, 2
D)
4, 4, 6, 5, 3
Đáp án
C
Câu 6
Trong cách biểu diễn đồ thị bằng danh sách cạnh chúng ta lưu trữ
A)
Danh sách tất cả các cạnh.
B)
Danh sách tất cả các đỉnh.
C)
Danh sách tất cả các cạnh và các đỉnh.
D)
Không lưu trữ danh sách cạnh và đỉnh nào.
Đáp án
A
Câu 7
Trong biểu diễn đồ thị bằng danh sách kề, mỗi danh sách kề chứa
A)
Các cạnh kề với một đỉnh.
Bản quyền windows 8, windows 7, Antivirus giá rẻ http://buykeysoft.blogspot.com
B)
Các đỉnh kề với một đỉnh.
C)
Tất cả các đỉnh kề và cạnh kề với nó.
D)
Các bậc của đỉnh kề với một đỉnh.
Đáp án
B
Câu 8
Tổng tất cả các bậc trong một đồ thị vô hướng bằng
A)
Hai lần số cạnh.
B)
Hai lần số đỉnh.
C)
Trung bình cộng của số đỉnh và số cạnh.
D)
Tổng của số đỉnh và số cạnh.
Đáp án
A
Câu 9
Nếu bậc của mỗi đỉnh trong đồ thị đều chẵn thì
A)
Đồ thị là liên thông.
B)
Đồ thị không liên thông.
C)
Tính liên thông của đồ thị không xác định.
D)
Đồ thị là liên thông mạnh
Đáp án
C
Câu 10
Đồ thị dưới dạng ma trận kề:
0 1 1 0 0
1 0 0 1 1
1 0 0 1 0
0 1 1 0 1
0 1 0 1 0

฀
฀
฀
฀
฀
฀
฀
Là đồ thị
A)
Euler
B)
Hamilton và Euler
C)
Hamilton
D)
không liên thông
Đáp án
C
Câu 11
Đồ thị dưới dạng ma trận kề:
0 1 1 1 0
1 0 0 1 1
1 0 0 1 0
1 1 1 0 1
0 1 0 1 0

฀
฀
฀
฀
฀
฀
฀
Là đồ thị
A)
nửa Euler
B)
Euler
C)
không liên thông
D)
Hamilton và Euler
Đáp án
A
Câu 12
Cho đồ thị được biểu diễn bởi ma trận kề sau đây
Bản quyền windows 8, windows 7, Antivirus giá rẻ http://buykeysoft.blogspot.com
00011
00111
0 1 0 0 1
11000
11100

฀
฀
฀
฀
฀
฀
฀
Danh sách các đỉnh nào dưới đây tạo nên đường đi trong đồ thị
A)
1, 3, 5, 2, 4
B)
1, 5, 3, 2, 4
C)
3, 4, 2, 5, 1
D)
3, 1, 5, 2, 4
Đáp án
B
Câu 13
Cho đồ thị được biểu diễn bởi ma trận kề sau đây
00011
00111
0 1 0 0 1
11000
11100

฀
฀
฀
฀
฀
฀
฀
Danh sách các đỉnh nào dưới đây tạo nên chu trình trong đồ thị
A)
1, 4, 5, 3, 2, 1
B)
1, 5, 4, 2, 3, 1
C)
1, 4, 2, 3, 5, 1
D)
1, 3, 5, 2, 4, 1
Đáp án
C
Câu 14
Cho đồ thị vô hướng G = (V,E), khẳng định nào sau đây là đúng?
A)
Thuật toán DFS(u) duyệt tất cả các đỉnh của đồ thị trong cùng thành phần
liên thông với đỉnh u
B)
Thuật toán DFS(u) luôn tìm ra được đường đi giữa hai đỉnh bất kì của đồ
thị
C)
Thuật toán DFS(u) duyệt tất cả các thành phần liên thông của đồ thị
D)
Thuật toán DFS(u) duyệt tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần
Đáp án
A
Câu 15
Cho đồ thị vô hướng G = (V,E), khẳng định nào sau đây là đúng?
A)
Thuật toán BFS(u) duyệt tất cả các thành phần liên thông của đồ thị
B)
Thuật toán BFS(u) luôn tìm ra được đường đi giữa hai đỉnh bất kì của đồ
thị
C)
Thuật toán BFS(u) duyệt tất cả các đỉnh của đồ thị trong cùng thành phần
liên thông với đỉnh u
D)
Thuật toán BFS(u) duyệt tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần
Đáp án
C
Câu 16
Đồ thị K4 có số đỉnh và số cạnh tương ứng là
A)
4,6
B)
4,8
C)
5,8
Bản quyền windows 8, windows 7, Antivirus giá rẻ http://buykeysoft.blogspot.com
D)
4,4
Đáp án
A
Câu 17
Phát biểu nào sau đây là sai khi nói đến đồ thị phân đôi đầy đủ Km,n
A)
có tập đỉnh được phân thành hai tập con tương ứng có m đỉnh và n đỉnh.
B)
có một cạnh giữa hai đỉnh nếu và chỉ nếu một đỉnh thuộc tập con này và đỉnh
thứ hai thuộc tập con kia.
C)
có một cạnh giữa hai đỉnh nếu và chỉ nếu mỗi đỉnh đều thuộc vào hai tập
đỉnh con.
D)
có m+n đỉnh, mn cạnh.
Đáp án
C
Câu 18
Đồ thị có đường đi vô hướng Euler khi và chỉ khi
A)
liên thông và có hai đỉnh bậc lẻ.
B)
không liên thông và có hai đỉnh bậc lẻ.
C)
liên thông và có một đỉnh bậc lẻ.
D)
không liên thông và không có đỉnh bậc lẻ.
Đáp án
A
Câu 19
Đồ thị phân đôi đầy đủ Kn,m có số màu bằng:
A)
3
B)
4
C)
2
D)
2
Đáp án
C
Câu 20
Đường đi Euler vô hướng trên một đồ thị có đỉnh đầu và đỉnh cuối
A)
trùng nhau
B)
khác nhau
C)
có cùng bậc chẵn
D)
Đỉnh đầu bậc chẵn đỉnh cuối bậc lẻ
Đáp án
B
Câu 21
Nếu G là đồ thị Euler thì
A)
không có đỉnh bậc chẵn
B)
không có đường đi Euler.
C)
không có chu trình Euler
D)
có chu trình Euler
Đáp án
D
Câu 22
Số màu của đồ thị Cn (với n chẵn) là
A)
1
B)
2
C)
3
D)
4
Đáp án
B
Câu 23
Số màu của đồ thị Cn (với n lẻ) là
A)
1
B)
2
C)
3
D)
4
Bản quyền windows 8, windows 7, Antivirus giá rẻ http://buykeysoft.blogspot.com
Đáp án
C
Câu 24
Chu trình Hamilton là
A)
Chu trình đi qua tất cả các đỉnh mỗi đỉnh đúng một lần trừ đỉnh bậc lẻ
B)
chu trình đi qua tất cả các đỉnh mỗi đỉnh đúng một lần trừ đỉnh bậc chẵn
C)
chu trình đi qua tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần
D)
chu trình đi qua tất cả các đỉnh của đồ thị mỗi đỉnh hơn một lần
Đáp án
C
Câu 25
Đồ thị liên thông G có một đỉnh có bậc bằng một thì
A)
G có chu trình Hamilton
B)
G có chu trình Euler
C)
G không có chu trình Hamilton
D)
G không có chu trình
Đáp án
C
Câu 26
Khi xây dựng chu trình Hamilton, nếu lấy hai cạnh liên thuộc với một đỉnh
đặt vào chu trình thì
A)
có thể xóa tất cả các cạnh còn lại không liên thuộc với đỉnh đó.
B)
có thể xóa tất cả các cạnh còn lại liên thuộc với đỉnh đó.
C)
có thể xóa tất cả các cạnh còn lại của đồ thị.
D)
có thể lấy thêm các cạnh liên thuộc với đỉnh đó.
Đáp án
B
Câu 27
Số màu trong đồ thị hình bánh xe Wn (với n chẵn) là
A)
1
B)
2
C)
3
D)
4
Đáp án
C
Câu 28
Số màu trong đồ thị hình bánh xe Wn (với n lẻ) là
A)
1
B)
2
C)
3
D)
4
Đáp án
D
Câu 29
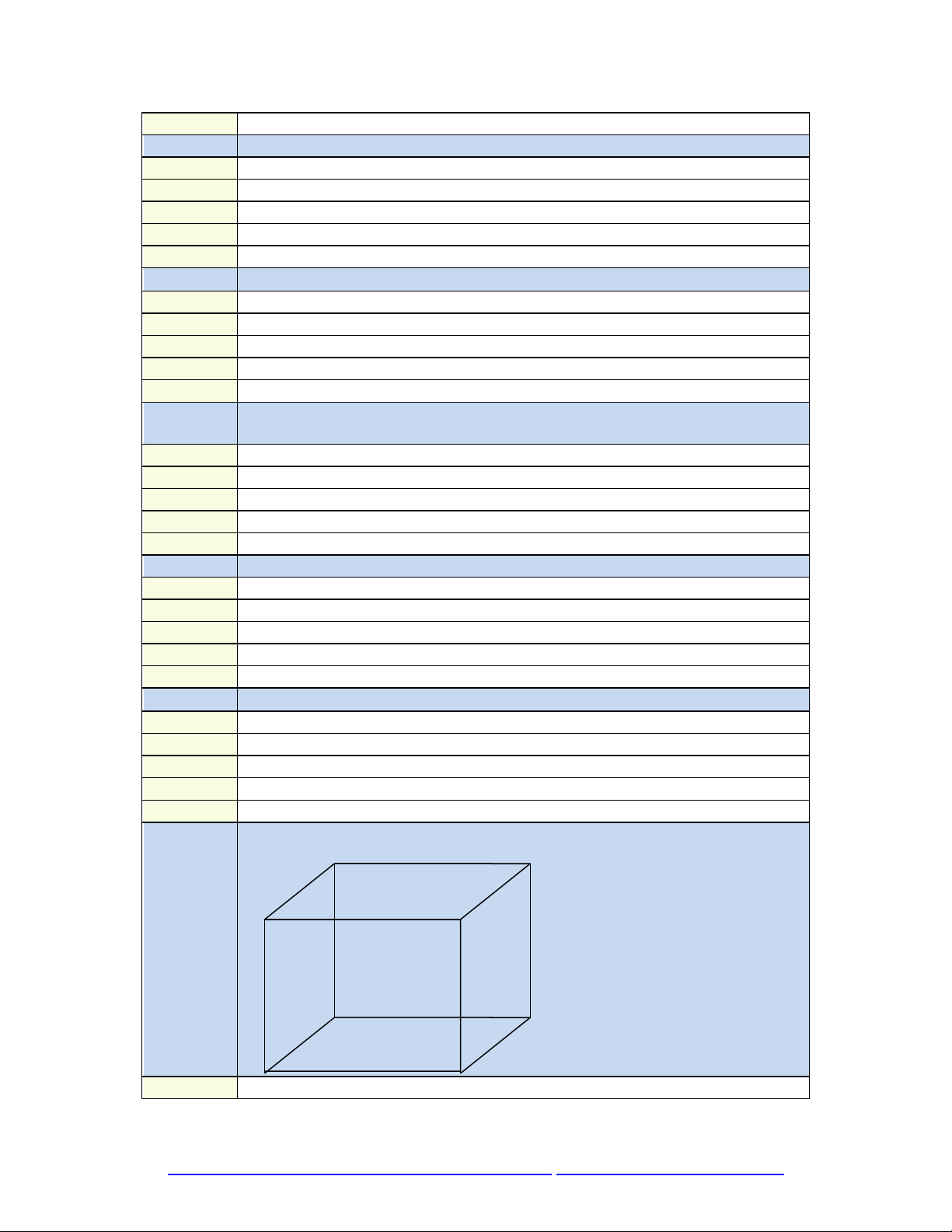
Cho đồ thị như hình vẽ hỏi đồ thị đó có phải là đồ thị phẳng hay không?
A)
Là đồ thị phẳng