Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 6
10/4/2011
Giảng viên Nguyễn Duy Khương 1
CHƯƠNG 4 Ứng suấtvàbiếndạng
3. Trạng thái ứng suấtphẳng
Ứng suất pháp lớnnhất‐Ứng suất chính
Thành phầnứng suất pháp lớnnhấtvànhỏnhất, ta gọiđây là ứng suất
chính. Để tìm thành phầnứng suấtchính,talấyđạo hàm của
x1 theo góc
và cho đạohàmnàybằng không
2
tan 2 xy
P
x
y
1()sin22cos20
x
xy xy
d
d
Nên ta được:
Với
Plà góc chính. Từcông thứctrêntatínhđược hai giá trị
Pvì thếta có
hai góc chính. Mộtgócchínhsẽcó mộtứng suất chính lớnnhấtvàgóc
chính còn lạihơnkém90
osẽcó ứng suất chính nhỏnhất. Hai ứng suất
chính này nằm trên hai mặt vuông góc nhau.
CHƯƠNG 4 Ứng suấtvàbiếndạng
3. Trạng thái ứng suấtphẳng
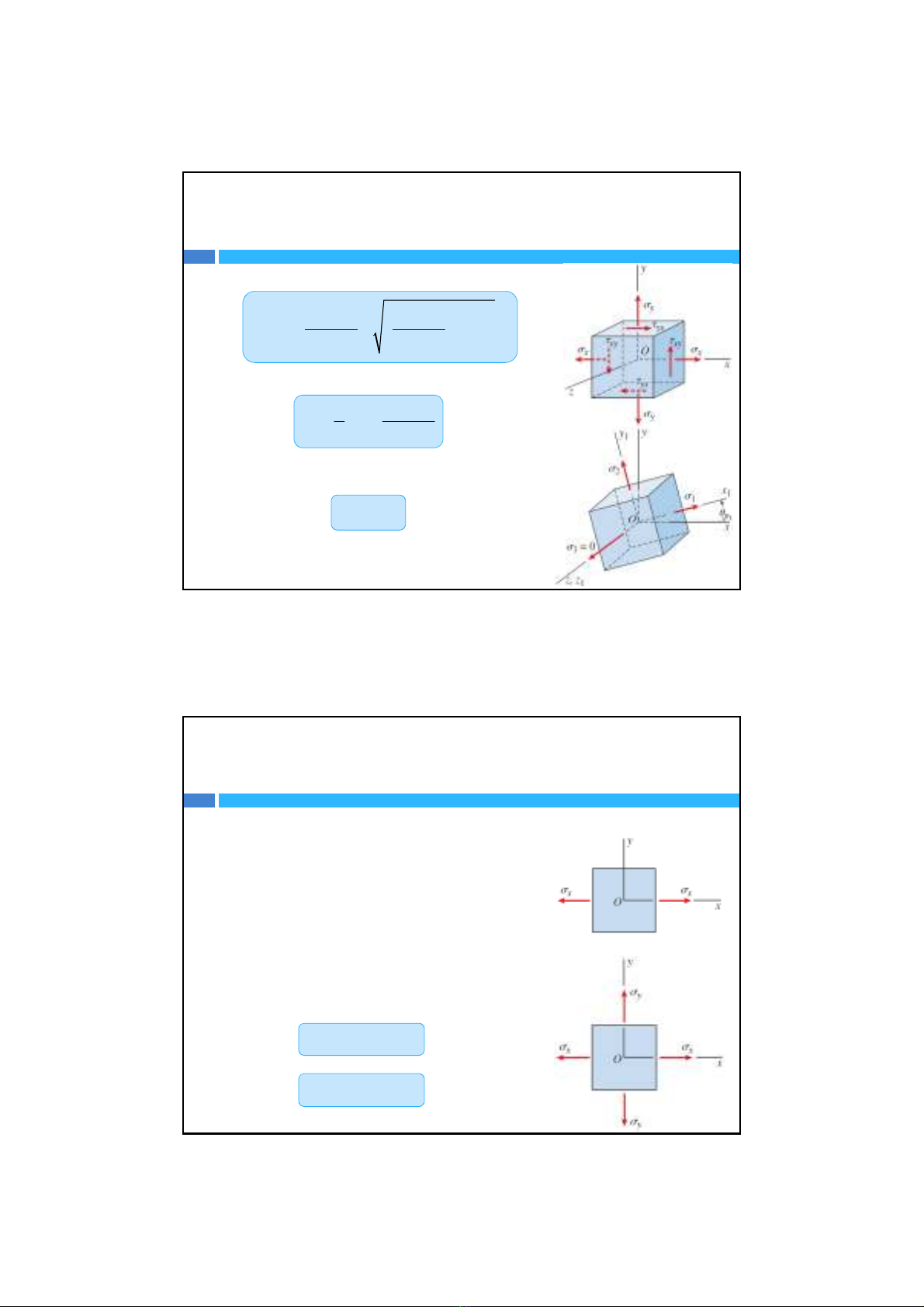
Và theo công thứctrênvàhệthứclượng trong tam giác vuông ta được
Vì thếta được
sin 2
x
y
P
R
cos 2 2
x
y
P
R
2
2
2
xy
x
y
R
Thếcông thức tính sin và cos vào công thứctínhứng suấtpháptrênmặt
nghiêng bấtkỳta được
2
2
122
xy xy
x
y
Mà ta có điềukiệntổng ứng suất pháp trên hai mặtnghiêngbấtkỳlà hằng số
2
2
12 2 1 22
xy xy
x
yxy xy
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 6
10/4/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 4 Ứng suấtvàbiếndạng
3. Trạng thái ứng suấtphẳng
Nên ta đượccôngthứctínhứng suất chính
2
2
1,2 22
xy xy
x
y
Ứng vớigócchính
12
1tan
2
xy
P
x
y
Ứng vớigócchínhnày,tadễdàng tính đượcứng
suấttiếptrênphương chính
0
xyP
Vậyứng suấtpháptrênphương chính đạtgiátrị
lớnnhấtvànhỏnhấtthìứng suấttiếptrên
phương chính bằng không.
CHƯƠNG 4 Ứng suấtvàbiếndạng
3. Trạng thái ứng suấtphẳng
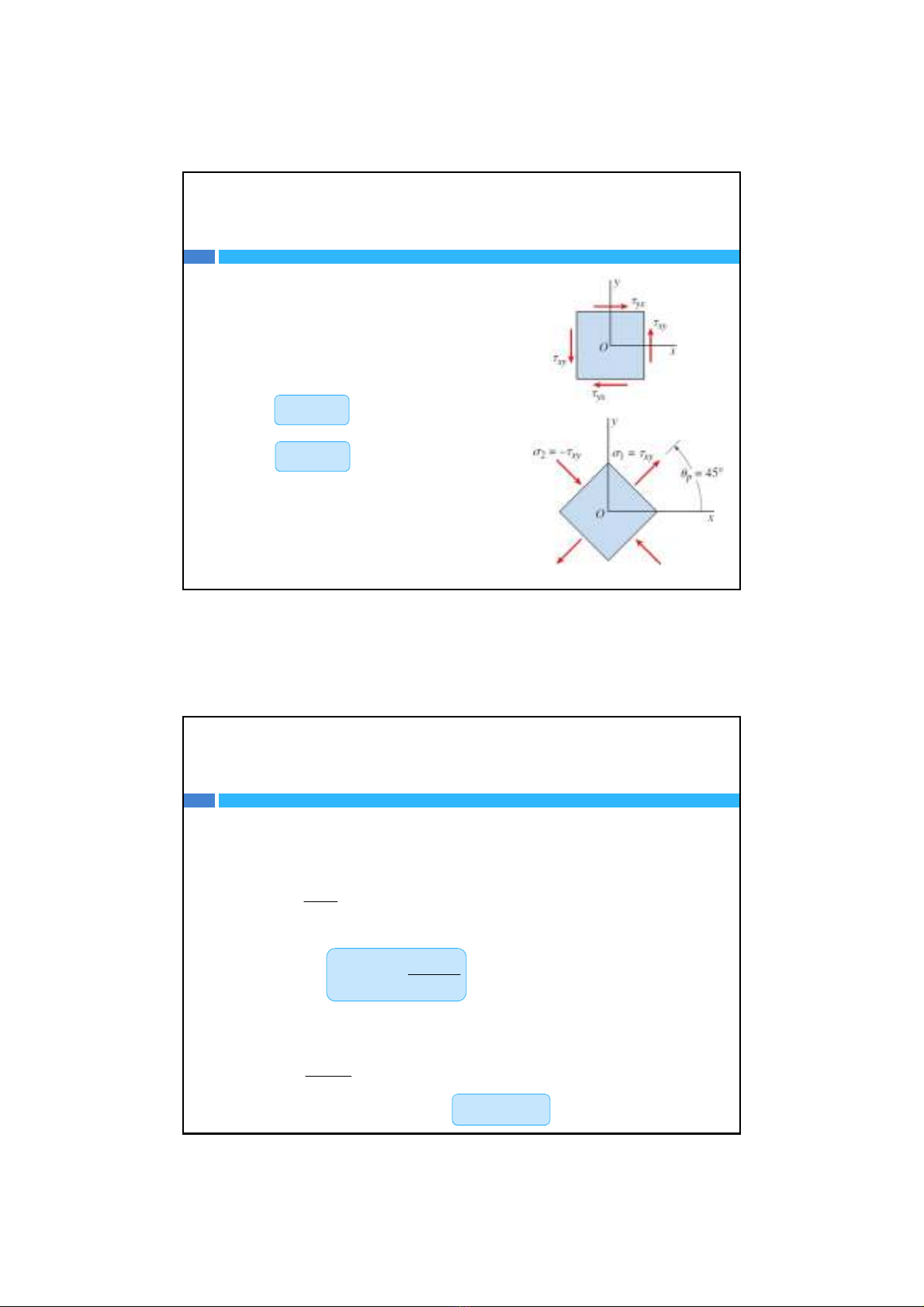
Ứng suấtđơntrụcvàsongtrục
Trường hợpđặcbiệt
Mặt chính trong cảhai trường hợpnàycũng chính
là mặt vuông góc vớitrụcxvàyvì
Đồng thời trên hai mặtxvàytathấyrằng ứng suất
tiếpbằng không. Vì thếthành phầnứng suấtchính
cũng bằng thành phầnứng suấtđơntrụcvàsong
trục.
1max( , )
x
y
2min( , )
x
y
tan 2 0 0 ,90
oo
PP
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 6
10/4/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 4 Ứng suấtvàbiếndạng
3. Trạng thái ứng suấtphẳng
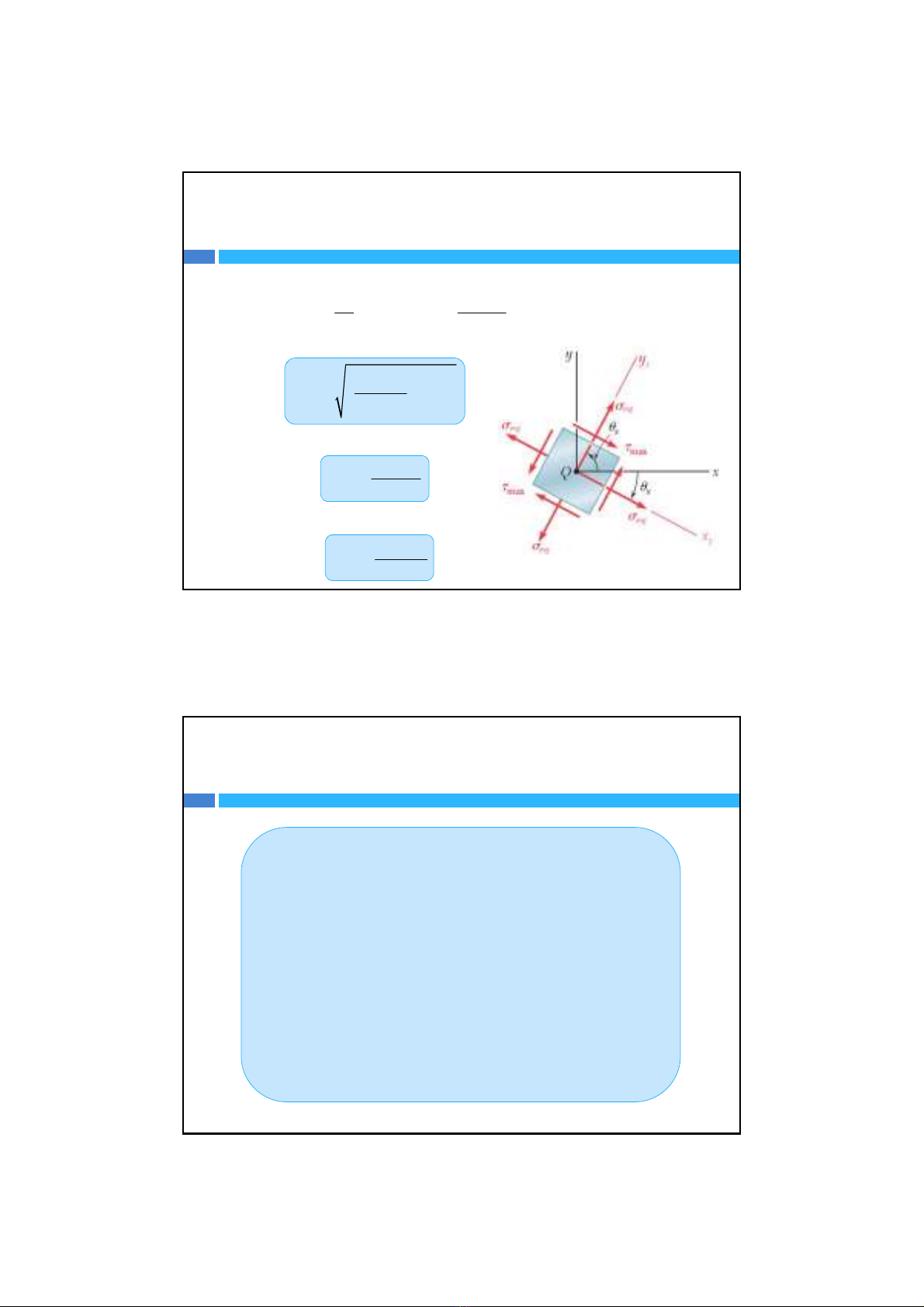
Ứng suấttrượtthuầntúy
Góc chính:
tan 2 45 ,135
oo
PP
Nếuứng suấttiếp
xy>0 thì
1
x
y
2
x
y
CHƯƠNG 4 Ứng suấtvàbiếndạng
3. Trạng thái ứng suấtphẳng
Ứng suấttiếplớnnhất
Để tìm thành phầnứng suấttiếplớnnhấtvàphương củanó,talấyđạo
hàm của
x1y1 theo góc
và cho đạohàmnàybằng không
tan 2 2
x
y
S
xy
11 ()cos22sin20
xy
xy xy
d
d
Nên ta được:
Với
Slà góc mà ứng suấttiếptrênmặtphẳng đósẽlà lớnnhất.
Từcông thứctrênvàcôngthứctínhgóc
Pta thấyrằng
1
tan 2 cot 2
tan 2
SP
P
cos(2 2 ) 0
SP
45o
SP
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 6
10/4/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 4 Ứng suấtvàbiếndạng
3. Trạng thái ứng suấtphẳng
Trên mặtcóứng suấttiếplớnnhấtdương
11
45o
SP
1
cos 2
x
y
SR
sin 2 2
x
y
SR
Nên ứng suấttiếplớnnhấtcógiátrị
2
2
max 2
xy
x
y
Hoặctínhtheoứng suất chính
1và
2
12
max 2
Ứng suất pháp trên mặt nghiêng này là
2
x
y
avg
CHƯƠNG 4 Ứng suấtvàbiếndạng
3. Trạng thái ứng suấtphẳng
ĐIỀUQUANTRỌNG CẦNNHỚ
•Ứng suấtchínhđượcxemnhưlà ứng suất pháp lớnnhấtvà
nhỏnhấttạimộtđiểm.
•Khi trạng thái ứng suấtđượcbiểudiễnlàứng suấtchínhthì
không có ứng suấttiếp tác dụng lên phầntử.
•Trạng thái ứng suấttạimộtđiểmcóthểđượcbiểudiễnbằng
ứng suấttiếplớnnhất. Trong trường hợpnàyứng suất pháp
trung bình sẽtác dụng lên phầntử.
•Phầntửđượcbiểudiễndướidạng ứng suấttiếplớnnhấtvà
ứng suất pháp trung bình thì sẽhợpmộtgóc45
ovớiphầntử
biểudiễndướidạng ứng suất chính.
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 6
10/4/2011
Giảng viên Nguyễn Duy Khương 5
CHƯƠNG 4 Ứng suấtvàbiếndạng
3. Trạng thái ứng suấtphẳng
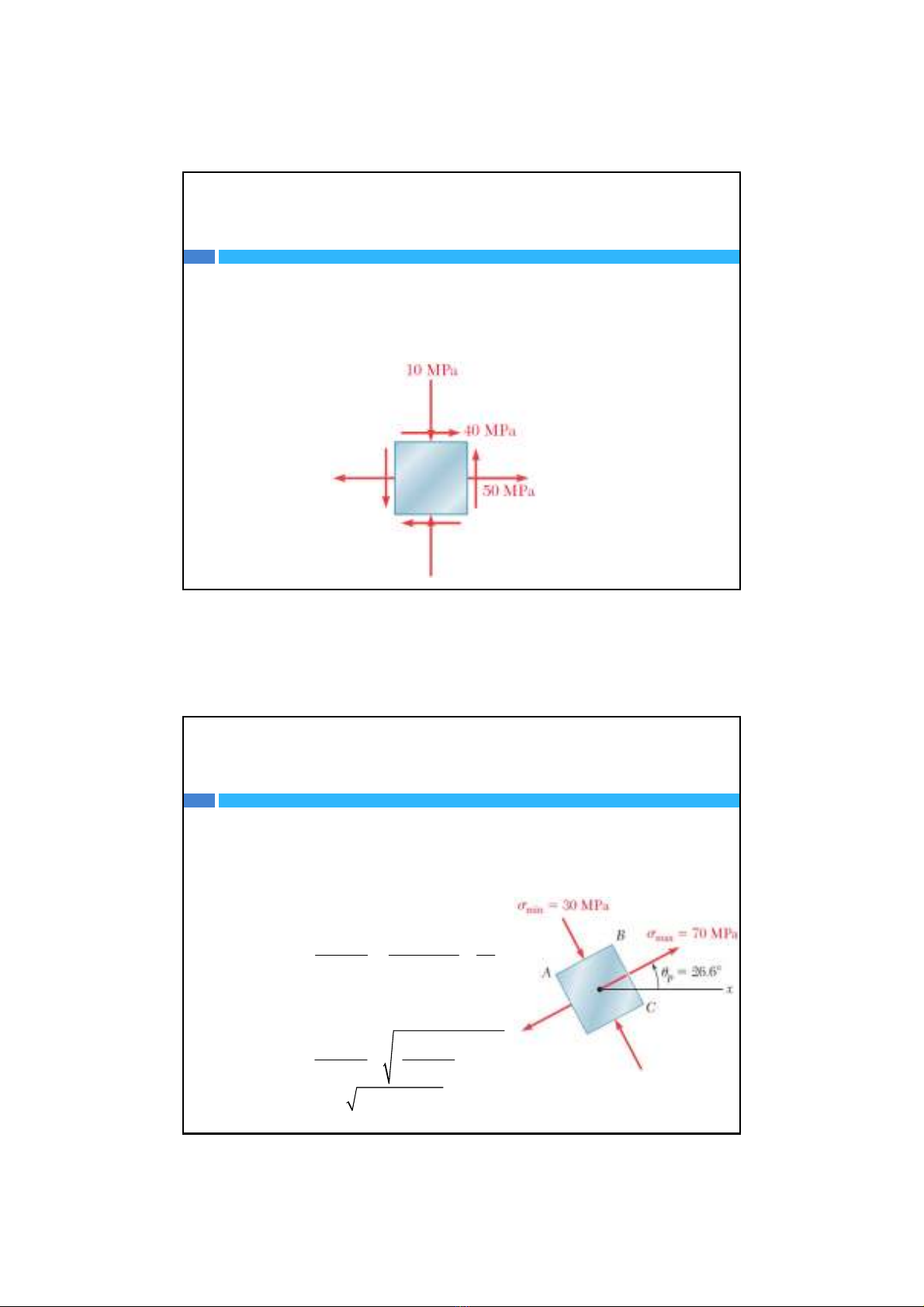
Ví dụ: Cho phân tốchịutrạng thái ứng suấtnhưhình vẽ.
a) Tìm phương chính.
b) Tìm ứng suất chính.
c) Tìm ứng suấttiếplớnnhấtvàứng suất pháp tương ứng.
CHƯƠNG 4 Ứng suấtvàbiếndạng
3. Trạng thái ứng suấtphẳng
Xác định các thành phầnứng suất
50 (MPa)
x
Phân tốchịuứng suấtphẳng nên ta có ba thành phầnứng suất
10 (MPa)
y
40 (MPa)
xy
Theo công thứctínhphương chính ta được
Tìm phương chính
2
tan 2 xy
P
x
y
2( 40) 80
50 ( 10) 60
26,6 và 116, 6
oo
P
Tìm ứng suất chính
2
2
max,min 22
xy xy
x
y
22
20 (30) (40) max min
70 MPa và 30 MPa











![Giáo trình Solidworks nâng cao: Phần nâng cao [Full]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260128/cristianoronaldo02/135x160/62821769594561.jpg)




![Giáo trình Vật liệu cơ khí [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250909/oursky06/135x160/39741768921429.jpg)









