Thuyết đồng dạng và
Phương pháp phân tích thứ nguyên
Bộ môn QT-TB CN Hóa học & Thực phẩm
Trường Đại học Bách khoa Hà nội

Thuy t đng d ng và Ph ng pháp phân tích th nguyênế ồ ạ ươ ứ
•Dùng đ nghiên c u chuy n quy mô c a các quá trình s n xu t: ể ứ ể ủ ả ấ
Phòng thí nghi m – Pilot (bán s n xu t) – S n xu t (công nghi p)ệ ả ấ ả ấ ệ
•Phòng TN: tìm ra các thông s thích h p c a quá trình: tố ợ ủ o, P, xúc tác, …
•Chuy n quy mô: tăng kích th c thi t b , th i gian th c hi n, …ể ướ ế ị ờ ự ệ
•Ph ng pháp nghiên c u quá trình và thi t b b ng mô hình th c ươ ứ ế ị ằ ự
nghi m g i là ệ ọ ph ng pháp mô hìnhươ
-Khi chuy n quy mô: mô hình trong s n xu t, pilot đng d ng v i mô ể ả ấ ồ ạ ớ
hình trong phòng thí nghi m, d a trên Lý thuy t đng d ngệ ự ế ồ ạ
-Th c ch t là ph ng pháp đúc k t, khái quát hóa các s li u th c ự ấ ươ ế ố ệ ự
nghi m đ rút ra các quy lu t chung cho các quá trình đng d ng v i ệ ể ậ ồ ạ ớ
nhau
1. Những điều kiện đồng dạng
I. Thuyết đồng dạng
Các hi n t ng ệ ượ đng d ng nhauồ ạ khi t l c a các đi l ng t ng t đc tr ng ỷ ệ ủ ạ ượ ượ ự ặ ư
c a chúng là đi l ng không đi theo 4 đi u ki n sau:ủ ạ ượ ổ ề ệ
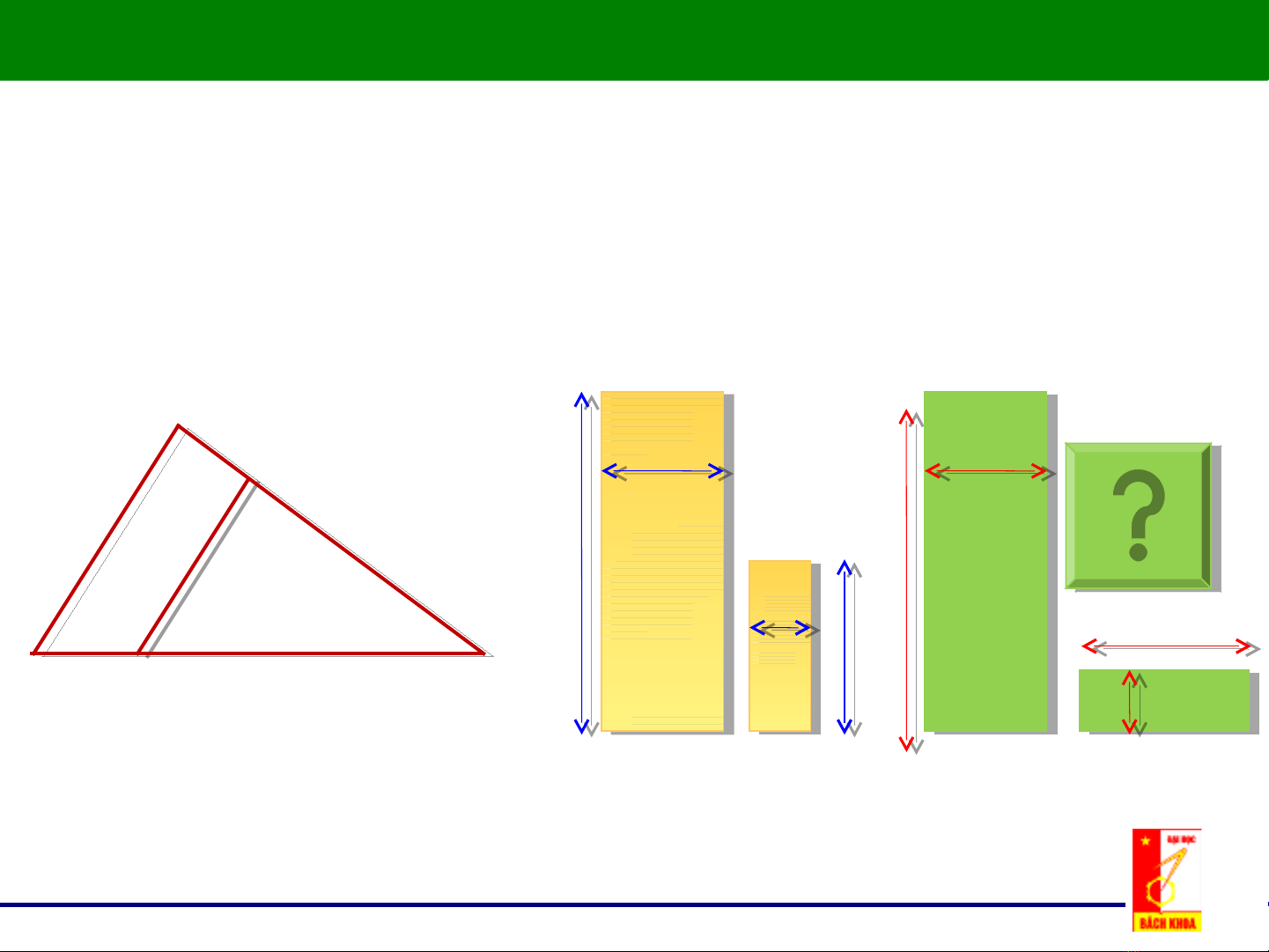
a. Đng d ng hình h cồ ạ ọ : hai v t đng d ng v hình h c khi kích th c t ng ậ ồ ạ ề ọ ướ ươ
ng ứsong song v i nhau và có ớt l không điỷ ệ ổ
L1
L3
L2
l1
l2
l3
L1/l1 = L2/l2 = L3/l3 = al = const
D/d = H/h = al = const
H
DD
H
d
d
h
h
a - h ng s đng d ng ằ ố ồ ạ
H ng s đng d ngằ ố ồ ạ là t l gi a hai đi l ng t ng ng c a hai h đng ỉ ệ ữ ạ ượ ươ ứ ủ ệ ồ
d ngạ

I. Thuyết đồng dạng
+ Đng d ng v th i gianồ ạ ề ờ : T l gi a các kho ng th i gian mà nh ng đi m ỷ ệ ữ ả ờ ữ ể
hay nh ng ph n t c a h th ng đng d ng chuy n đng theo nh ng quĩ ữ ầ ử ủ ệ ố ồ ạ ể ộ ữ
đo đng d ng hình h c là m t đi l ng không điạ ồ ạ ọ ộ ạ ượ ổ
1/ ’1 = 2/ ’2 = 3/ ’3 = aτ τ τ τ τ τ τ = const
+ Đng d ng v t lýồ ạ ậ : Nh ng thông s v t lý c a hai đi m hay hai ph n t ữ ố ậ ủ ể ầ ử
t ng ng trong h th ng đng d ng v không gian và th i gian có t l ươ ứ ệ ố ồ ạ ề ờ ỷ ệ
gi a nh ng đi l ng cùng lo i là m t đi l ng không điữ ữ ạ ượ ạ ộ ạ ượ ổ
w1/w’1 = w2/w’2 = w3/w’3 = aw = const
1/ ’1 = 2/ ’2 = 3/ ’3 = aρ ρ ρ ρ ρ ρ ρ = const
+ Đng d ng v đi u ki n đu và đi u ki n biênồ ạ ề ề ệ ầ ề ệ : nh ng đi u ki n đu ữ ề ệ ầ
và đi u ki n biên c a hai h đng d ng nhau cũng ph i đng d ng v i ề ệ ủ ệ ồ ạ ả ồ ạ ớ
nhau.
2. Định số đồng dạng và chuẩn số đồng dạng
I. Thuyết đồng dạng
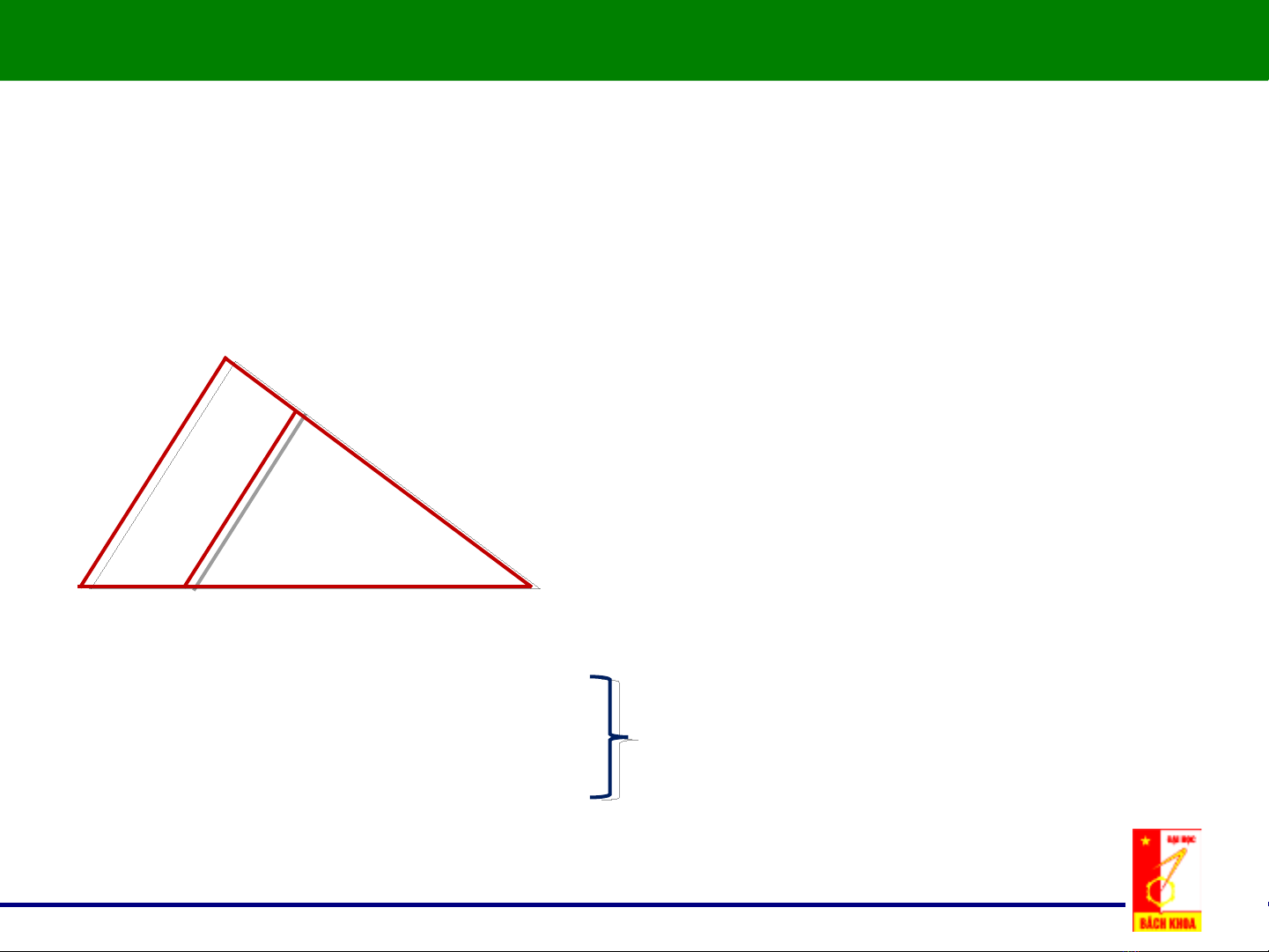
T l c a 2 đi l ng cùng ki u, t i 2 đi m khác nhau c a cùng m t ỷ ệ ủ ạ ượ ể ạ ể ủ ộ
h th ng v i m t h th ng đng d ng là m t đi l ng không đi ệ ố ớ ộ ệ ố ồ ạ ộ ạ ượ ổ
L1
L3
L2
l1
l2
l3
L1/L3 = l1/l3 = i’l = const
a - h ng s đng d ng ằ ố ồ ạ
i - đnh s đng d ng (đn h )ị ố ồ ạ ơ ệ Là các đi l ng không có th ạ ượ ứ
nguyên
L1/l1 = L2/l2 = L3/l3 = al = const
L1/L2 = l1/l2 = il = const
L2/L3 = l2/l3 = i’’l = const






![Bài giảng Hóa công 1: Chương mở đầu - TS. Cao Thị Mai Duyên [Full]](https://cdn.tailieu.vn/images/document/thumbnail/2023/20230201/kimphuong59/135x160/6021675245936.jpg)